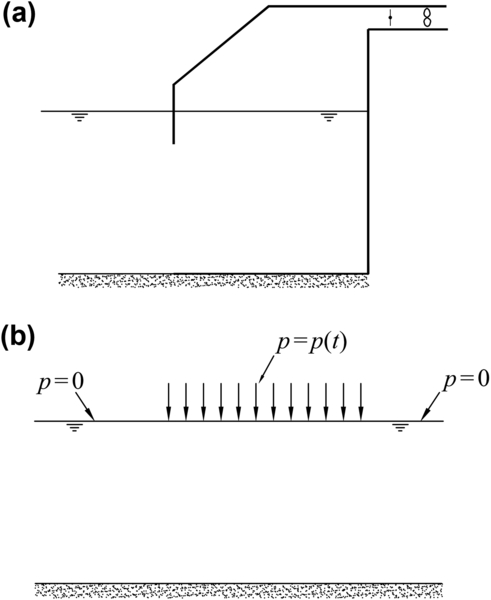
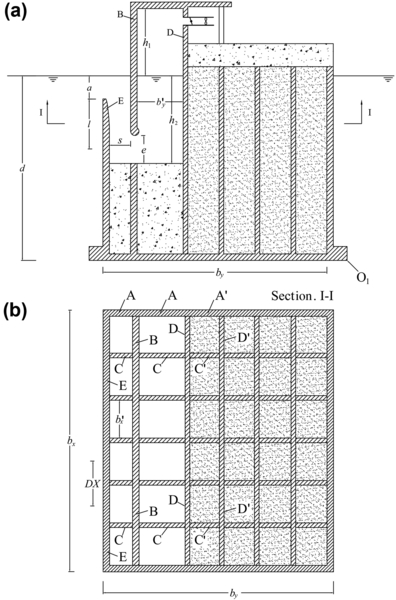
Many immersed oscillating systems have been disclosed for the aim of wave energy conversion. One of the first was a navigation buoy due to the pioneering research of Commander Yoshio Masuda in Japan. It consisted of a battery-charging generator driven by an oscillating water column (OWC) contained in a vertical pipe through a floating buoy. Masuda's developmental work of this device was in the mid-1960s (see
ECOR, 2003;
Falcao, 2010, for more details). The research of the 1970s concentrated mainly on resonant point absorbers (
McCormick, 1974;
Mei, 1976;
Budal and Falnes, 1975,
1977). Two well-known devices of those years were the “Salter duck” (
Salter, 1974) and the “Bristol cylinder” (
Evans, 1976). According to the classification of
Hagerman (1995), these belong, respectively, to the class of “pitching floats with mutual force reaction” and “submerged buoyant absorbers with sea-floor reaction point.” Starting from the 1980s, most international attention was focused on fixed OWCs, whose prototypes were built in Australia, China, India, Japan, Norway, Portugal, and the United Kingdom. A conventional fixed OWC is essentially a box with a large opening on the wave-beaten wall. This opening usually goes from the seabed to nearly the mean water level (see the scheme of
Fig. 15.1(a)). An air pocket remains between the roof and sea surface and is connected to the atmosphere by an exhaust tube with a turbine. Typically, this is a Wells turbine that rotates in the same direction even if the direction of the air flow is reversed (
Raghunathan, 1995). Calculation of the performances of these kind of plants (
Evans, 1982;
Sarmento and Falcao, 1985) is founded on one pillar, that is, Stoker's solution (
1957) for the waves generated by an oscillating pressure applied uniformly over a segment of the water surface (
Fig. 15.1(b)). A first criticality of conventional OWCs is that their eigenperiod is smaller than the wave period. To overcome this problem, some devices were developed to create a sort of artificial resonance. This is known as “latching control” (
Korde, 1991,
2002;
Falcao and Justino, 1999). However, artificial resonance cannot compare with natural resonance. A second criticality of conventional OWCs deals with the stability of the structure. The geometry of conventional OWCs is different from the geometry of well-established structural types, such as, for example, offshore gravity platforms or caisson breakwaters. Hence, in designing a conventional OWC, we cannot exploit a consolidated experience, and this enhances the risk of failure; indeed, some failures must be registered among
the prototypes (see
ECOR, 2003). To overcome these criticalities, the author (
2007a) introduced the U-OWC (see
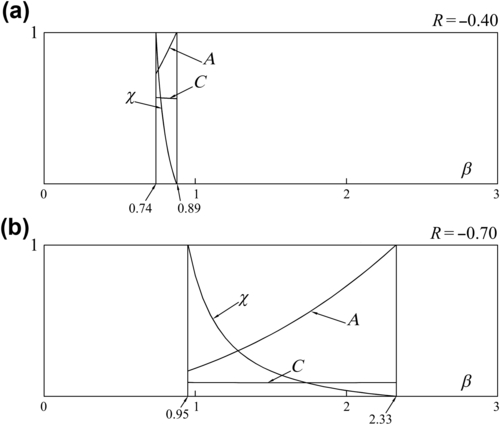
Fig. 15.2). Not only eigenperiods of U-OWCs are greater than eigenperiods of conventional OWCs, but the designer may tune the eigenperiod at his choice, on playing on the ratios
s/b′y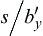
and
s/
l. As to the overall stability, the design of U-OWCs can exploit the great experience accumulated with the design of caisson breakwaters (see
Chapter 14). These are two evident pros for passing from conventional OWCs to U-OWCs. The cons should reduce themselves to the fact that Stoker's solution can no longer be exploited. Indeed, here there are not
two adjacent segments, one with a pulsating pressure and one with the atmospheric pressure, like in
Fig. 15.1(a) and (b). This is because of the presence of the vertical duct connecting the sea with the chamber. This implies the need of leaving the territory explored initially by
Lamb (1905), disclosed by
Stoker (1957), further enlightened by
Wehausen and Laitone (1960), and entering an unknown territory. Finding a solution for the interaction between wave and U-OWC took the author 2
years of work. The results were published in the paper (
2007b) and are reproposed here below in a revised form.
![]() (15.1)
(15.1)![]() (15.2)
(15.2)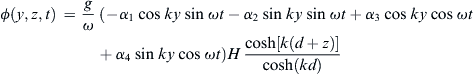 (15.3)
(15.3)![]() (15.4)
(15.4)![]() (15.5)
(15.5)![]() (15.6)
(15.6)![]() (15.7)
(15.7)![]() (15.8)
(15.8)![]() (15.9)
(15.9)![]() (15.10)
(15.10)![]() (15.11)
(15.11) (15.12)
(15.12)![]() (15.13)
(15.13)![]()
![]() (15.14)
(15.14)
![]() (15.15)
(15.15)![]() (15.16)
(15.16)![]() (15.17)
(15.17)![]() (15.18)
(15.18)
![]() (15.19)
(15.19)![]() (15.20)
(15.20)![]() (15.21)
(15.21)![]() (15.22)
(15.22)![]() (15.23)
(15.23)![]() (15.24)
(15.24)![]() (15.25)
(15.25)![]() (15.26)
(15.26)![]() (15.27)
(15.27)![]() (15.28)
(15.28)![]() (15.29)
(15.29)![]() (15.30)
(15.30)![]() (15.31)
(15.31)![]() (15.32)
(15.32)![]() (15.33)
(15.33)![]() (15.34)
(15.34)![]() (15.35)
(15.35)![]() (15.36)
(15.36)![]() (15.37)
(15.37)![]() (15.38)
(15.38)![]() (15.39)
(15.39)![]() (15.40)
(15.40)