Calculation of Wave Forces on Gravity Platforms and Submerged Tunnels
Abstract
The general method of Chapter 10 for calculating the largest wave forces on large isolated bodies of arbitrary shape is applied. This method (being based on QD theory and SSFEs) is much simpler than the commonly applied methods using Green's functions, which are summarized in the conclusive notes to the chapter. The first part of the chapter deals with an estimate of the largest wave loads on a gravity offshore platform, in a design sea state. A worked example is given, and a FORTRAN program is supplied that calculates the resultant wave force as a function of time. The second part of the chapter deals with an estimate of the largest wave loads on a submerged tunnel, in a design sea state. Here too, a worked example is given and a FORTRAN program is supplied. This program gives the distributions of the wave force per unit length, at a number of time instants, during the transit of the wave group of the maximum expected wave height.
Keywords
Offshore gravity platform; Quasi-determinism theory (QD); Small-scale field experiment (SSFE); Submerged tunnel; Wave load13.1. Wave Forces on a Gravity Offshore Platform
13.1.1. Calculation of the Diffraction Coefficient
![]()
![]()

13.1.2. Calculation of the Wave Force
File PLATGEO
140.0 d
60.0 HTANK (height vertical cylinders)
110.0 HCOL (height columns)
20.0 DCYL (diameter vertical cylinders)
20.0 DCOL1 (greater diameter column)
14.0 DCOL2 (smaller diameter column)
19 number of vertical cylinders
coordinates centers cylinders:
| 0.0 | −40.0 |
| 17.3 | −30.0 |
| 34.6 | −20.0 |
| 34.6 | 0.0 |
| 34.6 | 20.0 |
| Table Continued | |

| 17.3 | 30.0 |
| 0.0 | 40.0 |
| −17.3 | 30.0 |
| −34.6 | 20.0 |
| −34.6 | 0.0 |
| −34.6 | −20.0 |
| −17.3 | −30.0 |
| 0.0 | −20.0 |
| 17.3 | −10.0 |
| 17.3 | 10.0 |
| 0.0 | 20.0 |
| −17.3 | 10.0 |
| 0.0 | −10.0 |
| 0.0 | 0.0 |

c 3 number of columns
c coordinates centers columns:
| 0.0 | −20.0 |
| 17.3 | 10.0 |
| −17.3 | 10.0 |
PROGRAM PLAT
CHARACTER∗64 NOMEC
DIMENSION XCI(20),YCI(20)
DIMENSION XCO(10),YCO(10)
COMMON D,HS,H,TP,TST,ALPHA,TETAD,RNP
COMMON IMAX,JMAX,OMV(300),TETV(150),RKV(300)
COMMON SOT(300,150)
NOMEC='PLATGEO'
.OPEN(UNIT=50,STATUS='OLD',FILE=NOMEC)
READ(50,∗)D
READ(50,∗)HTANK
READ(50,∗)HCOL
READ(50,∗)DCYL
READ(50,∗)DCOL1
READ(50,∗)DCOL2
READ(50,∗)NCYL
READ(50,∗)
DO N=1,NCYL
READ(50,∗)XCI(N),YCI(N)
ENDDO
READ(50,∗)NCOL
READ(50,∗)
DO N=1,NCOL
READ(50,∗)XCO(N),YCO(N)
ENDDO
NOMEC='FORCE2'
OPEN(UNIT=60,FILE=NOMEC)
PG=3.141592
DPG=2.∗PG
WRITE(6,∗)'Hs,H'
READ(5,∗)HS,H
WRITE(6,∗)'alpha,thetad(degree),np'
READ(5,∗)ALPHA,TETAD,RNP
WRITE(6,∗)'zero up-crossing wave -> 1, down-crossing -> -1'
READ(5,∗)UD
TETAD=TETAD∗PG/180.
WRITE(6,∗)'diffraction coefficients base and columns'
READ(5,∗)CDBA,CDCO
RO=1.03E3
DTAU=0.02
NCALL=0
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
c this call of QD, with NCALL=0, serves to store the directional spectrum.
NCALL=1
DO 100 J=1,126
c Loop 100: time
TAU=−1.25+FLOAT(J-1)∗DTAU
T=TAU∗TP
c FX x-component Froude-Krylov force on the base of the platform
c FY y-component Froude-Krylov force on the base of the platform
FX=0
FY=0
DO 400 N=1,NCYL
c Loop 400: vertical cylinders of the base
R=DCYL/2
X=XCI(N)
Y=YCI(N)
DS=HTANK/10
DO 500 I=1,10
c each vertical cylinder is subdivided into 10 pieces;
c loop 500 covers these 10 pieces.
Z=-D+FLOAT(I-1)∗DS+DS/2
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
COFI=RO∗PG∗R∗R∗DS
FX=FX+COFI∗AX
FY=FY+COFI∗AY
500 CONTINUE
400 CONTINUE
c effect of the interstices among the vertical cylinders
FBX=FX∗1.065
FBY=FY∗1.065
c step from Froude-Krylov force to force on the solid body (base)
FBX=FBX∗CDBA
FBY=FBY∗CDBA
c conversion from N to kN
FBX=FBX∗1.E−3
FBY=FBY∗1.E−3
c Here the calculation of the wave force on the base has been completed.
c Now the calculation of the wave force on the columns starts
c FX x-component Froude-Krylov force on the columns
c FY y-component Froude-Krylov force on the columns
FX=0
FY=0
DO 410 N=1,NCOL
c Loop 410 columns
X=XCO(N)
Y=YCO(N)
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
HCOLW=d-HTANK
DS=(HCOLW+ETA)/20
DO 510 I=1,20
c the wet portion of a column is subdivided into 20 pieces;
c loop 510 covers these 20 pieces
ZI=FLOAT(I-1)∗DS+DS/2.
Z=-HCOLW+ZI
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
DIAM=DCOL1+(DCOL2-DCOL1)∗ZI/HCOL
R=DIAM/2
.COFI=RO∗PG∗R∗R∗DS
FX=FX+COFI∗AX
FY=FY+COFI∗AY
510 CONTINUE
410 CONTINUE
c step from Froude-Krylov force to force on the solid body (columns)
FCX=FX∗CDCO
FCY=FY∗CDCO
c conversion from N to kN
FCX=FCX∗1.E-3
FCY=FCY∗1.E-3
c Here the calculation of the wave force on the columns has been completed
c FTX is the x-component of the wave force on the whole structure
c FTY is the y-component of the wave force on the whole structure
FTX=FBX+FCX
FTY=FBY+FCY
WRITE(60,1000)TAU,FTX,FTY
WRITE(6,1000)TAU,FTX,FTY
1000 FORMAT(2X,F7.2,2X,E12.4,2X,E12.4)
100 CONTINUE
WRITE(6,∗)
WRITE(6,∗)'read results on file FORCE2'
END
13.2. Wave Forces on a Submerged Tunnel
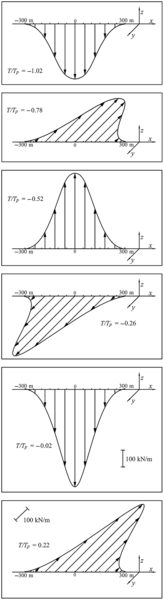
13.2.1. Wave Height and Diffraction Coefficients
![]()
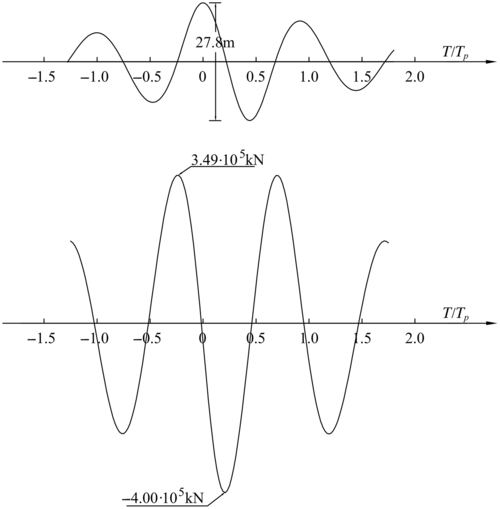
![]()

13.2.2. Calculation of Wave Force
PROGRAM TUNN
CHARACTER∗64 NOMEC
DIMENSION FYV(300),FZV(300),TAUV(300)
DIMENSION FPYV(300,200),FPZV(300,200)
COMMON D,HS,H,TP,TST,ALPHA,TETAD,RNP
COMMON IMAX, JMAX,OMV(300),TETV(150),RKV(300)
COMMON SOT(300,150)
NOMEC='LOAD1'
OPEN(UNIT=60,FILE=NOMEC)
PG=3.141592
DPG=2.∗PG
WRITE(6,∗)'Hs,H'
READ(5,∗)HS,H
WRITE(6,∗)'alpha,thetad(degree),np'
READ(5,∗)ALPHA,TETAD,RNP
WRITE(6,∗)'zero up-crossing wave -> 1, down-crossing -> -1'
READ(5,∗)UD
TETAD=TETAD∗PG/180
WRITE(6,∗)'horizontal and vertical diffraction coefficients'
READ(5,∗)CDO,CDV
RO=1.03E3
D=125.
c DIAM diameter tunnel
c ZCE z tunnel center
c RLT length of tunnel being considered
DIAM=25
R=DIAM/2.
ZCE=−42.5
RLT=600.
DX=RLT/60.
DTAU=0.02
.NCALL=0
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
c this call of QD, with NCALL=0, serves to store the directional spectrum
NCALL=1
DO 100 J=1,156
c Loop 100:time
TAU=-1.30+FLOAT(J-1)∗DTAU
WRITE(6,5010)TAU
5010 FORMAT(2X,F7.2)
TAUV(J)=TAU
T=TAU∗TP
c FYV(J) resultant wave force (y-component) on the piece
c of tunnel being considered
c FZV(J) resultant wave force (z-component) on the piece
c of tunnel being considered
FYV(J)=0
FZV(J)=0
DO 400 N=1,61
c Loop 400:X (axis tunnel)
X=-RLT/2.+FLOAT(N-1)∗DX
Y=0
Z=ZCE
CALL QD(NCALL,UD,X,Y,Z,T,VX,VY,VZ,AX,AY,AZ,ETA)
COFI=RO∗PG∗R∗R
c FPYV(J,N) wave force per unit length (y-component)
c FPZV(J,N) wave force per unit length (z-component)
FPYV(J,N)=CDO∗RO∗PG∗R∗R∗AY
FPZV(J,N)=CDV∗RO∗PG∗R∗R∗AZ
c conversion from N to kN
FPYV(J,N)=1.E-3∗FPYV(J,N)
FPZV(J,N)=1.E-3∗FPZV(J,N)
FYV(J)=FYV(J)+FPYV(J,N)∗DX
FZV(J)=FZV(J)+FPZV(J,N)∗DX
400 CONTINUE
100 CONTINUE
DO 600 J=2,154
c Loop 600: time
c tau=TAUV(J)
c |Fy(tau-dtau)|=AFY1
c |Fy(tau)|=AFY2
c |Fy(tau+dtau)|=AFY3
AFY1=ABS(FYV(J-1))
AFY2=ABS(FYV(J))
AFY3=ABS(FYV(J+1))
IF(AFY2.GT.AFY1.AND.AFY2.GT.AFY3)THEN
c a local maximum (or minimum) of Fy has been found
WRITE(60,1000)TAUV(J)
1000 FORMAT(//,6X,'TAU = ',F7.2,4X,'(fy)',/)
DO 490 N=1,61
c Loop 490:X (axis tunnel)
X=-RLT/2.+FLOAT(N-1)∗DX
WRITE(60,1001)X,FPYV(J,N)
1001 FORMAT(2X,F6.0,2X,F6.1)
490 CONTINUE
ENDIF
c |Fz(tau-dtau)|=AFZ1
c |Fz(tau)|=AFZ2
c |Fz(tau+dtau)|=AFZ3
AFZ1=ABS(FZV(J-1))
AFZ2=ABS(FZV(J))
AFZ3=ABS(FZV(J+1))
IF(AFZ2.GT.AFZ1.AND.AFZ2.GT.AFZ3)THEN
c a local maximum (or minimum) of Fz has been found
WRITE(60,1002)TAUV(J)
1002 FORMAT(//,6X,'TAU = ',F7.2,4X,'(fz)',/)
DO 491 N=1,61
c Loop 491:X (axis tunnel)
X=-RLT/2.+FLOAT(N-1)∗DX
WRITE(60,1001)X,FPZV(J,N)
491 CONTINUE
ENDIF
600 CONTINUE
WRITE(6,∗)
WRITE(6,∗)'read results on file LOAD1'
END