8.1. The Necessary and Sufficient Condition for the Occurrence of a Wave Crest of Given Very Large Height
The condition
η(to)=b
 (8.1)
(8.1)
where
to is a given time instant and
b is a given positive value, in the limit as
b/
σ →
∞, and is not only necessary but also sufficient in probability for the occurrence of a wave crest of given height
b. (“A is sufficient in probability for the occurrence of B” means that “given A, the probability approaches 1 that B occurs.”)
Actually, the necessary and sufficient condition in probability is
η(to)=b,η˙(to)=0
 (8.2)
(8.2)
However, the reasoning we are going to do is the same whether starting from condition
(8.1) or from condition
(8.2), and the conclusion is exactly the same. The advantage in dealing with condition
(8.1) rather than with condition
(8.2) is that one works with a 2
×
2 covariance matrix rather than 3
×
3, so the mathematical steps are lighter.
In order to prove that condition
(8.1) is sufficient, let us consider the conditional probability of the surface elevation at any fixed time instant
to +
T given condition
(8.1). We have
p[η(to+T)=u|η(to)=b]=p[η(to)=b,η(to+T)=u]p[η(to)=b]
 (8.3)
(8.3)
From Section
4.2 we know that
p[η(to)=b,η(to+T)=u]=12πM√exp[−12M(M11b2+2M12bu+M22u2)]
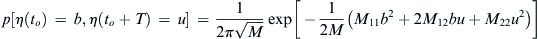 (8.4)
(8.4)
p[η(to)=b]=12πm0√exp(−b22m0)
 (8.5)
(8.5)
Hence, it follows that
p[η(to+T)=u|η(to)=b]=m02πM−−−−√exp[F(u)]
 (8.6)
(8.6)
where F(u) denotes the function
F(u)=−12M(M11b2+2M12bu+M22u2)+b22m0
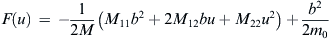 (8.7)
(8.7)
which may be rewritten in the form
F(u)=−M222M(u−um)2+F(um)
 (8.8)
(8.8)
where um is the abscissa of the maximum:
um=−M12M22b
 (8.9)
(8.9)
(The determinant and the
i,
i cofactors of a covariance matrix are positive, and this is why we have concluded that the function
F(
u) has a maximum.) From Eqns
(8.6) and
(8.8) we get
p[η(to+T)=u|η(to)=b]=m02πM−−−−√exp[F(um)]exp[−M222M(u−um)2]
 (8.10)
(8.10)
Now let us obtain the cofactors Mij and the determinant M. The random variables here are η(to) and η(to + T) and hence the covariance matrix is
CM=(m0ψ(T)ψ(T)m0)
 (8.11)
(8.11)
so that
M11=m0,M22=m0,M12=−ψ(T),M=m20−ψ2(T)
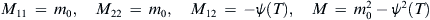 (8.12)
(8.12)
Here, it can be proven that
F(
um)
=
0. However, this proof is not strictly necessary for our goal, so that we limit ourselves to note that the random variable
η(
to +
T), given condition
(8.1), has the following:
CONDITIONALAVERAGE=um
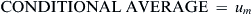 (8.13)
(8.13)
CONDITIONALSTANDARDDEVIATION=MM22−−−√
 (8.14)
(8.14)
which implies
CONDITIONALAVERAGE=ψ(T)ψ(0)b
 (8.15)
(8.15)
CONDITIONALSTANDARDDEVIATION<σ
 (8.16)
(8.16)
The conditional average is a deterministic function of T; that is,
η¯(to+T)=ψ(T)ψ(0)b
 (8.17)
(8.17)
Since the standard deviation of the random surface elevation with respect to this deterministic function is smaller than
σ, the random function
η(
to +
T) is asymptotically equal to the deterministic function
η¯(to+T)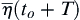
, if
b/
σ tends to infinity. Finally, given that
η¯(to+T)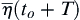
has its absolute maximum at
to, and this maximum is
b, we conclude that condition
(8.1) is sufficient for the occurrence of a wave crest of given height
b, if
b/
σ →
∞.
8.2. A Sufficient Condition for the Occurrence of a Wave of Given Very Large Height
The condition
η(to)=H2,η(to+T∗)=−H2
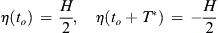 (8.18)
(8.18)
where
to is a given time instant and
H is a given positive value, in the limit as
H/
σ →
∞ is sufficient and necessary in probability for the occurrence of a wave of given height
H. Actually, this is not exactly the sufficient and necessary condition in probability. As to being sufficient: given condition
(8.18) (with
H/
σ →
∞) the probability approaches 1 to have the occurrence of a wave height
H plus a very small random difference of order (
H/
σ)
−1σ. As to being necessary: given a very large wave height
H, the probability approaches 1 that the following occur:
η(to)=(12+δξ)H,η(to+T∗)=(−12+δξ)H
 (8.19)
(8.19)
with
δξ
being a very small random difference of order (
H/
σ)
−1. However, these very small random differences are negligible for the conclusions of this chapter. (They become nonnegligible in the problem of the probability of wave heights leading to Eqn
(4.44). Sections 9.7–9.10 of a previous book by the author (
2000) may serve to deepen this item.)
In order to prove that condition
(8.18) is sufficient, let us consider the conditional probability of the surface elevation at any fixed time instant
to +
T given condition
(8.18). We have
p[η(to+T)=u|η(to)=H2,η(to+T∗)=−H2]=p[η(to)=H2,η(to+T∗)=−H2,η(to+T)=u]p[η(to)=H2,η(to+T∗)=−H2]
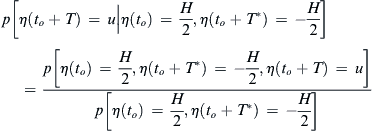 (8.20)
(8.20)
From Section
4.2 we know that
p[η(to)=12H,η(to+T∗)=−12H,η(to+T)=u]=1(2π)3/2M√exp{−12M[M33u2+2(M13−M23)12Hu+(M11+M22−2M12)14H2]},
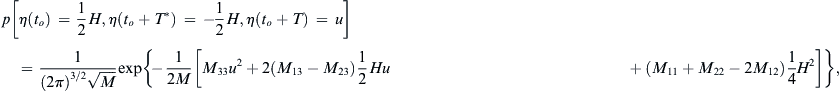 (8.21)
(8.21)
p[η(to)=12H,η(to+T∗)=−12H]=12πM˜√exp[−12M˜(M˜11+M˜22−2M˜12)14H2],
 (8.22)
(8.22)
where
Mij and
M are the
i,
j cofactor and the determinant of the covariance matrix of
η(
to),
η(to+T∗)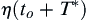
,
η(
to +
T); that is,
CM=⎛⎝⎜ψ(0)ψ(T∗)ψ(T)ψ(T∗)ψ(0)ψ(T−T∗)ψ(T)ψ(T−T∗)ψ(0)⎞⎠⎟,
 (8.23)
(8.23)
and
M˜ij
and
M˜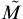
are the
i,
j cofactor and the determinant of the covariance matrix of
η(
to),
η(to+T∗)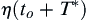
. (Note that
M˜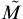
is equal to
M33.) Hence, it follows that
p[η(to+T)=u|η(to)=H2,η(to+T∗)=−H2]=M332πM−−−−√exp[F(u)]
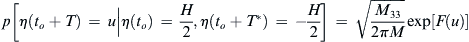 (8.24)
(8.24)
where F(u) here denotes the function
F(u)=−12M[M33u2+2(M13−M23)12Hu+(M11+M22−2M12)14H2−MM33(M˜11+M˜22−2M˜12)H24]
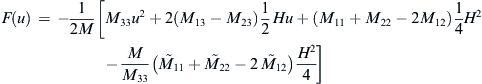 (8.25)
(8.25)
which may be rewritten in the form
F(u)=−M332M(u−um)2+F(um)
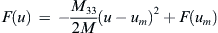 (8.26)
(8.26)
where um is the abscissa of the maximum:
um=M23−M13M33H2
 (8.27)
(8.27)
From Eqns
(8.24) and
(8.26) we get
p[η(to+T)=u|η(to)=H2,η(to+T∗)=−H2]=M332πM−−−−√exp[F(um)]⋅exp[−M332M(u−um)2]
 (8.28)
(8.28)
Now let us obtain the cofactors
Mij and the determinant
M of the covariance matrix Eqn
(8.23). When dealing with large covariance matrices it is convenient to resort to some compact symbols for the entries of these matrices. In this case let us define
a=ψ(0),b=ψ(T∗),c=ψ(T),d=ψ(T−T∗)
 (8.29)
(8.29)
so that the covariance matrix and the relevant cofactors are reduced to
CM=⎛⎝⎜abcbadcda⎞⎠⎟
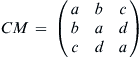 (8.30)
(8.30)
M11=a2−d2
 (8.31)
(8.31)
M12=cd−ab
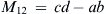 (8.32)
(8.32)
M13=bd−ac
 (8.33)
(8.33)
M23=bc−ad
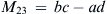 (8.34)
(8.34)
M33=a2−b2
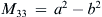 (8.35)
(8.35)
M=a(a2−d2)+b(cd−ab)+c(bd−ac)
 (8.36)
(8.36)
Here, it can be proven that
F(
um)
=
0. However, this proof is not strictly necessary for our goal, so that we limit ourselves to note that the random variable
η(
to +
T), given condition
(8.18), has
CONDITIONALAVERAGE=um
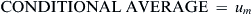 (8.37)
(8.37)
CONDITIONALSTANDARDDEVIATION=MM33−−−√
 (8.38)
(8.38)
which implies
CONDITIONALAVERAGE=c−da−bH2
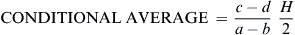 (8.39)
(8.39)
CONDITIONALSTANDARDDEVIATION<σ
 (8.40)
(8.40)
Later we shall prove the inequality Eqn
(8.40).
The conditional average is a deterministic function of T, that is,
η¯(to+T)=ψ(T)−ψ(T−T∗)ψ(0)−ψ(T∗)H2
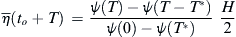 (8.41)
(8.41)
Since the standard deviation of the random surface elevation with respect to this deterministic function is smaller than
σ, the random function
η(
to +
T) is asymptotically equal to the deterministic function
η¯(to+T)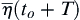
, if
H/
σ tends to infinity. Since
1.
η¯(to+T)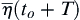
has its absolute maximum at
to, and this maximum is
H/2;
2.
η¯(to+T)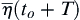
has its absolute minimum at
to+T∗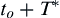
, and this minimum is
−H/2.
we conclude that condition
(8.18) is sufficient for the occurrence of a wave of given height
H, if
H/
σ →
∞. This is provided that the wave crest at
to and the wave trough at
to+T∗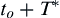
in the deterministic wave
η¯(to+T)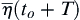
are the crest and trough of the same wave. Whether or not this condition is satisfied depends on the shape of the spectrum. This condition is satisfied with characteristic spectra of wind seas like JONSWAP or Pierson and Moskowitz.
It remains to prove the inequality Eqn
(8.40). We must prove that
a(a2−d2)+b(cd−ab)+c(bd−ac)a2−b2<a
 (8.42)
(8.42)
This may be rewritten in the form
a[1−c2+d2−2cd(ba)a2−b2]<a
 (8.43)
(8.43)
that is proven if we succeed in proving that
c2+d2−2cd(ba)>0
 (8.44)
(8.44)
Here we note that
−1<ba<0
 (8.45)
(8.45)
(b/a being the ratio between the absolute minimum and the absolute maximum of the autocovariance); as to the product cd it may be either positive or negative (according to the value of T). If cd > 0, the inequality is satisfied because the term −2cd(b/a) is greater than zero. If cd < 0 it follows that
c2+d2−2cd(ba)>c2+d2+2cd=(c+d)2>0
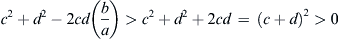 (8.46)
(8.46)
which completes the proof.
8.4. The First Deterministic Wave Function in Space and Time
“Given a very large wave crest of height b at a time instant to at a point xo, yo” is equivalent to given:
η(xo,yo,to)=b
 (8.61)
(8.61)
This is what proceeds from Section
8.1. Here let us consider the conditional probability of the surface elevation at any fixed point
xo +
X,
yo +
Y at time instant
to +
T, given condition
(8.61). We have
p[η(xo+X,yo+Y,to+T)=u|η(xo,yo,to)=b]=p[η(xo,yo,to)=b,η(xo+X,yo+Y,to+T)=u]p[η(xo,yo,to)=b]
 (8.62)
(8.62)
What is most important is that we make no restriction about whether the wave field is or is not homogeneous in space. For example, the wave field may be on the open sea, or before a long breakwater, or in the lee of a vertical breakwater.
Given that both
η(
xo,
yo,
to) and
η(
xo +
X,
yo +
Y,
to +
T) represent stationary Gaussian processes of time, the steps to be done are the same leading from Eqns
(8.1) to
(8.10), and the result is
p[η(xo+X,yo+Y,to+T)=u|η(xo,yo,to)=b]=M222πM−−−−√exp[−(M222M)(u−um)2]
 (8.63)
(8.63)
where
um=−M12M22b
 (8.64)
(8.64)
Now let us obtain the cofactors Mij and the determinant M. The random variables here are η(xo, yo, to) and η(xo + X, yo + Y, to + T) and hence the covariance matrix is
CM=(σ2(xo,yo)Ψ(X,Y,T;xo,yo)Ψ(X,Y,T;xo,yo)σ2(xo+X,yo+Y))
 (8.65)
(8.65)
We have
M11=σ2(xo+X,yo+Y)
 (8.66)
(8.66)
M22=σ2(xo,yo)
 (8.67)
(8.67)
M12=−Ψ(X,Y,T;xo,yo)
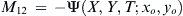 (8.68)
(8.68)
M=σ2(xo,yo)σ2(xo+X,yo+Y)−Ψ2(X,Y,T;xo,yo)
 (8.69)
(8.69)
The random surface elevation η(xo + X, yo + Y, to + T), given that η(xo, yo, to) = b, has
CONDITIONALAVERAGE=um
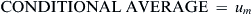 (8.70)
(8.70)
CONDITIONALSTANDARDDEVIATION=MM22−−−√
 (8.71)
(8.71)
which implies
CONDITIONALAVERAGE=Ψ(X,Y,T;xo,yo)σ2(xo,yo)b
 (8.72)
(8.72)
CONDITIONALSTANDARDDEVIATION<σ(xo+X,yo+Y)
 (8.73)
(8.73)
The conditional average is a deterministic wave function of X, Y, T that may be rewritten in the form
η¯(xo+X,yo+Y,to+T)=Ψ⌢(X,Y,T;xo,yo)[bσ(xo,yo)]σ(xo+X,yo+Y)
 (8.74)
(8.74)
where
Ψ⌢
is the cross-correlation whose range is (
−1,1) (cf. Section
7.3.3). From Eqn
(8.73) we know that the standard deviation of the random surface elevation with respect to this deterministic function is smaller than
σ(
xo +
X,
yo +
Y). Conclusion: the random surface elevation
η(
xo +
X,
yo +
Y,
to +
T) is asymptotically equal to the deterministic wave function
η¯(xo+X,yo+Y,to+T)
, as
b/
σ(
xo,
yo) tends to infinity.
It must be pointed out that there is no restriction on the ratio
σ(
xo +
X,
yo +
Y)/
σ(
xo,
yo). In particular,
xo,
yo may be a point in the lee of a breakwater and
xo +
X,
yo +
Y may be a point on the wave-beaten wall of the breakwater, so that the ratio
σ(
xo +
X,
yo +
Y)/
σ(
xo,
yo) is very large. Nevertheless, if we know that at point
xo,
yo a wave crest occurs with a height
b that is exceptionally large with respect to the root mean square surface elevation at this point, we may expect that the surface elevation at
xo +
X,
yo +
Y will be close to a well-defined deterministic wave function given by Eqn
(8.74). Hence, even if the wave crest recorded in the lee is much smaller than the waves at the outer wall, the fact of having found a wave crest that is exceptionally
large with respect to the average in the lee will enable us to predict how the waves are even at the outer wall.
8.5. The Velocity Potential Associated with the First Deterministic Wave Function in Space and Time
The form (Eqn
(8.74)) of the deterministic wave function is effective for understanding the sense of the QD theory; however, for calculation, the form
η¯(xo+X,yo+Y,to+T)=Ψ(X,Y,T;xo,yo)σ2(xo,yo)b
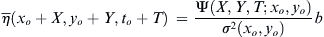 (8.75)
(8.75)
is more straightforward. Associated with this deterministic wave function is a distribution of velocity potential in the water, which to the lowest order in a Stokes expansion is given by
ϕ¯(xo+X,yo+Y,z,to+T)=Φ(X,Y,T,z;xo,yo)σ2(xo,yo)b
 (8.76)
(8.76)
The surface elevation (Eqn
(8.75)) and the velocity potential (Eqn
(8.76)) satisfy the linear flow equations. In particular, we shall prove that
η¯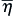
and
ϕ¯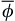
satisfy the first linear flow equation under the hypothesis that
η and
ϕ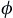
satisfy this equation. That is to say, we shall prove that
η¯=−1g(∂ϕ¯∂T)z=0
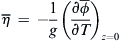 (8.77)
(8.77)
provided that
η=−1g(∂ϕ∂t)z=0
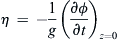 (8.78)
(8.78)
With the formulas
(8.75) and
(8.76) of
η¯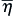
and
ϕ¯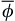
, the equality
(8.77) (to be proved) takes on the form
Ψ(X,Y,T;xo,yo)σ2(xo,yo)b=−1g[∂∂TΦ(X,Y,T,z;xo,yo)bσ2(xo,yo)]z=0
 (8.79)
(8.79)
where the term
b/
σ2(
xo,
yo) cancels. With the definitions (7.1) and (7.9) of
Ψ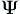
and
Φ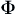
, the equality to be proved becomes
⟨η(xo,yo,to)η(xo+X,yo+Y,t+T)⟩=−1g[∂∂T⟨η(xo,yo,t)ϕ(xo+X,yo+Y,z,t+T)⟩]z=0
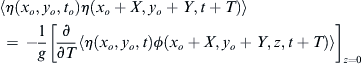 (8.80)
(8.80)
wherein the order “derivative with respect to
T,” “average with respect to
t” may be inverted, with the result that the equality to be proved becomes
⟨η(xo,yo,to)η(xo+X,yo+Y,t+T)⟩=[⟨η(xo,yo,t)(−1g)∂∂Tϕ(xo+X,yo+Y,z,t+T)⟩]z=0
and this equality is proved since
η(xo+X,yo+Y,t+T)=(−1g)∂∂Tϕ(xo+X,yo+Y,z,t+T)z=0
 (8.81)
(8.81)
as a consequence of Eqn
(8.78). Equation
(8.81) says that random surface elevation
η and the relevant velocity potential
ϕ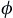
satisfy the linear flow Eqn
(8.78) at point
xo +
X,
yo +
Y, at time instant
t +
T.
8.6. The Second Deterministic Wave Function in Space and Time
“Given a very large wave of height H at a time instant to at a point xo, yo” is equivalent to
η(xo,yo,to)=H2,η(xo,yo,to+T∗)=−H2
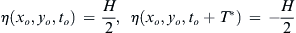 (8.82)
(8.82)
This is what proceeds from Sections
8.2 and
8.3.
Given condition
(8.82) as
H/
σ(
xo,
yo)
→
∞, the random surface elevation
η(
xo +
X,
yo +
Y,
to +
T) is asymptotically equal to the deterministic function
η¯(xo+X,yo+Y,to+T)=Ψ(X,Y,T;xo,yo)−Ψ(X,Y,T−T∗;xo,yo)Ψ(0,0,0;xo,yo)−Ψ(0,0,T∗;xo,yo)H2
 (8.83)
(8.83)
and the velocity potential associated with this deterministic wave function is
ϕ¯(xo+X,yo+Y,z,to+T)=Φ(X,Y,z,T;xo,yo)−Φ(X,Y,z,T−T∗;xo,yo)Ψ(0,0,0;xo,yo)−Ψ(0,0,T∗;xo,yo)H2
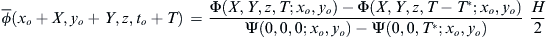 (8.84)
(8.84)
The deterministic wave function (Eqn
(8.83)) is obtained starting from condition
(8.82) and reasoning as in Section
8.4. Then with the same reasoning done in Section
8.5, one can verify that deterministic wave function (Eqn
(8.83)) and velocity potential (Eqn
(8.84)) satisfy the linear flow equations.
8.7. Comment: A Deterministic Mechanics Is Born by the Theory of Probability
Given a wave with a known height H, if H/σ is very large, the conditional standard deviation of the random surface elevation is negligible with respect to the conditional average surface elevation. This conditional average represents a deterministic wave function of space and time. Hence, the actual (random) waves will be very close to this deterministic wave function. Associated with this deterministic wave function is a very precise distribution of velocity potential in the water.
The conclusion is that a deterministic mechanics consisting of the deterministic wave function (Eqn
(8.83)) and the relevant velocity potential (Eqn
(8.84)) is born by the theory of probability.
What the author finds exciting is that Eqns
(8.83) and
(8.84) hold for an arbitrary configuration of the solid boundary (of course, provided that the flow is frictionless). Only the relationship between functions Ψ and Φ and the directional spectrum
S(
ω,
θ) of the incident waves changes with the solid boundary (several examples of this relationship are given in
Chapter 7).
The sense of the QD theory is the following: if a wave with an exceptionally large height H occurs at some point xo, yo at a time instant to, it is most probable that the occurrence of this wave happens in a very precise (deterministic) way.
Note that the assumption that given wave height H is very large with respect to σ of the sea state may be consistent with the Stokes assumption that the wave height is small with respect to the bottom depth and the wavelength. Of course, what has been said in this section regarding the wave of given height H conceptually holds also for the wave crest of given height b.
8.8. Conclusion
In the spring of 1980 the author realized that a wave with a given very large crest height in a Gaussian sea state is close to the autocovariance (Eqn
(8.17)) and published this result in papers (
1982,
1983). After this result the author wondered whether determinism can be born within a chaotic process. In fact, the result suggested two opposite conclusions. Let us review these conclusions in simple words; to do this we shall resort to the evidence of numbers. (The reader should bear in mind that we are dealing with a Gaussian random process of unlimited duration and unlimited wave height). Let us assume that the
ψ∗ of this stationary random Gaussian process is equal to 0.60. In this process, a wave with a crest height of b = 100
σ will
have a height H = 1.6 100
σ = 160
σ. Because of the statistical symmetry of the Gaussian process, a wave with an elevation of the trough of
−100
σ will have a profile opposite to that of the wave of crest height 100
σ. Hence a consequence of Eqn
(8.17) with our example is that
1. a wave of given crest height 100σ has a deterministic height of 160σ;
2. a wave of given height 160σ does not have a deterministic crest height: indeed, there is the same probability that this wave has a crest of 100σ or a trough of −100σ (which implies a crest of 60σ).
Item (1) suggests a positive conclusion: yes, determinism can be born within a chaotic process. Item (2) suggests the opposite conclusion. The author was able to solve this contradiction with the proof shown in Sections
8.2 and
8.3 of the present chapter: a wave of given very large height
H is close to the deterministic wave function
(8.41); what this implies, in our example, is that a wave of given height 160
σ has a deterministic crest height of 80
σ. This does not contradict what proceeds from Eqn
(8.17), since the number of wave crests of 100
σ is very small with respect to the number of wave heights of 160
σ. In other words, the set of waves having the given height of 160
σ consists of waves all with the crest height of 80
σ, except for a very small fraction of anomalous elements of the set. This very small fraction includes the whole set of waves with the given crest height of 100
σ. Hence, the general conclusion is: yes, determinism can be born within a chaotic process. This was called “quasi-determinism” because of the presence of the very small fractions of anomalous elements. The first time the term quasi-determinism appeared was in a paper by the author (
1984), where Eqn
(8.41) was also disclosed.
Some time later the author made substantial progress when Eqn
(8.83) was applied to the space-time; this was in 1986, and the publication was in the paper (
1989). Here, the author showed that a very large wave of given height
H occurs at some fixed point
xo,
yo because this point is struck home by a well-defined wave group. This group has a deterministic (new) mechanics that we shall analyze in detail in the next chapter. Finally, in June 1987 the author applied Eqn
(8.83) to Gaussian wave fields being nonhomogeneous in space (publication in the papers (
1988) and (
1997b)). It was an exciting experience! We shall see a few examples in
Chapter 11. In particular, we shall see that a very large wave of given height occurs at a fixed point
xo,
yo far from a long breakwater, because of a collision of two wave groups. The logic is that of quasi-determinism: if a wave with a given very large height will occur at some fixed point, we can predict, with a probability approaching 1, the story of this occurrence. This result implies that “a deterministic mechanics can be born within a chaotic process,” which is an
aspect of the possibility that determinism can be born within a chaotic process.
In the 1980s the author knew Rice’s work (
1944,
1945,
1958) on the analysis of stationary random Gaussian processes, and the author did not know some subsequent works on the same subject. In particular,
Lindgren (1972) had shown that the behavior of
ηb(
t) is well determined by the behavior of
ψ(
t) as
b → ∞, where
ηb is the random Gaussian function, given that at
t = 0 there is a local maximum of ordinate
b. This is essentially the same as Eqn
(8.17). However, the approach was different from the author’s: in his paper Lindgren focused on mathematical random functions, whereas in the papers (
1982,
1983) the author focused on waves. If the author had not reobtained independently Eqn
(8.17) through the approach focused on waves, the author would not have arrived at the QD theory. Professor Leon Borgman played an important role with an open-minded review of the author’s early work (acknowledged in the paper (
1983)).
The more difficult part of the basic proof of the QD theory is that concerning the necessary condition. The original forms the author gave in the 1980s were rather complicated, and only some years later (
1997a) the author reached the simple form that is given in Section
8.3 of this chapter.
![]() (8.1)
(8.1)![]() (8.2)
(8.2)![]() (8.3)
(8.3)![]() (8.4)
(8.4)![]() (8.5)
(8.5)![]() (8.6)
(8.6)![]() (8.7)
(8.7)![]() (8.8)
(8.8)![]() (8.9)
(8.9)![]() (8.10)
(8.10)![]() (8.11)
(8.11)![]() (8.12)
(8.12)![]() (8.13)
(8.13)![]() (8.14)
(8.14)![]() (8.15)
(8.15)![]() (8.16)
(8.16)![]() (8.17)
(8.17)![]() (8.18)
(8.18)![]() (8.19)
(8.19)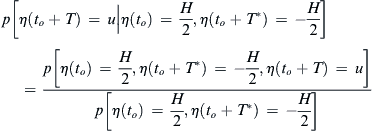 (8.20)
(8.20)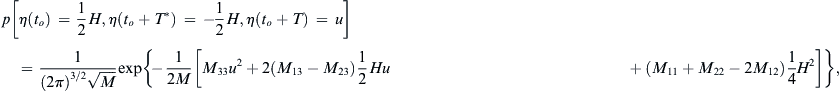 (8.21)
(8.21) (8.22)
(8.22) (8.23)
(8.23)![]() (8.24)
(8.24)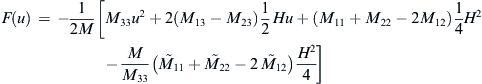 (8.25)
(8.25)![]() (8.26)
(8.26)![]() (8.27)
(8.27) (8.28)
(8.28)![]() (8.29)
(8.29)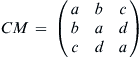 (8.30)
(8.30)![]() (8.31)
(8.31)![]() (8.32)
(8.32)![]() (8.33)
(8.33)![]() (8.34)
(8.34)![]() (8.35)
(8.35)![]() (8.36)
(8.36)![]() (8.37)
(8.37)![]() (8.38)
(8.38)![]() (8.39)
(8.39)![]() (8.40)
(8.40)![]() (8.41)
(8.41)![]() (8.42)
(8.42) (8.43)
(8.43)![]() (8.44)
(8.44)![]() (8.45)
(8.45)![]() (8.46)
(8.46)![]() (8.47)
(8.47)![]()
![]()
 (8.48)
(8.48)![]() (8.49)
(8.49)![]() (8.50)
(8.50)![]() (8.51)
(8.51)![]() (8.52)
(8.52)![]() (8.53)
(8.53)![]() (8.54)
(8.54)![]() (8.55)
(8.55)![]() (8.56)
(8.56)![]() (8.57)
(8.57)![]() (8.58)
(8.58)![]() (8.59)
(8.59)
![]()
![]()
 (8.60)
(8.60)![]() (8.61)
(8.61) (8.62)
(8.62) (8.63)
(8.63)![]() (8.64)
(8.64)![]() (8.65)
(8.65)![]() (8.66)
(8.66)![]() (8.67)
(8.67)![]() (8.68)
(8.68)![]() (8.69)
(8.69)![]() (8.70)
(8.70)![]() (8.71)
(8.71)![]() (8.72)
(8.72)![]() (8.73)
(8.73)![]() (8.74)
(8.74)![]() (8.75)
(8.75)![]() (8.76)
(8.76)![]() (8.77)
(8.77)![]() (8.78)
(8.78)![]() (8.79)
(8.79)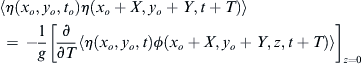 (8.80)
(8.80)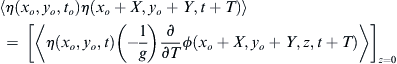
![]() (8.81)
(8.81)![]() (8.82)
(8.82)![]() (8.83)
(8.83)![]() (8.84)
(8.84)