QD Theory
Mechanics of Reflected and Diffracted Wave Groups
Abstract
An exceptionally large wave at some distance off a long vertical breakwater, most probably, is due to the collision of two wave groups: one going back seawards after having been reflected and one approaching the breakwater. An exceptionally large wave at the lee side of a breakwater, most likely, is due to a wave group that strikes the tip of the breakwater, and is broken into two halves, one of which penetrates the sheltered area, by diffraction. These are two of the predictions of the QD theory for what concerns random waves interacting with vertical breakwaters. The chapter shows these predictions, as well as the results of a verification by means of a small-scale field experiment.
Keywords
Long vertical breakwater; Nonhomogeneous wave field; Quasi-determinism theory (QD); Semi-infinite vertical breakwater; Small-scale field experiment (SSFE); Wave group11.1. Before a Breakwater
11.1.1. Equations of Deterministic Waves before an Upright Breakwater
 (11.1)
(11.1)
 (11.2)
(11.2)
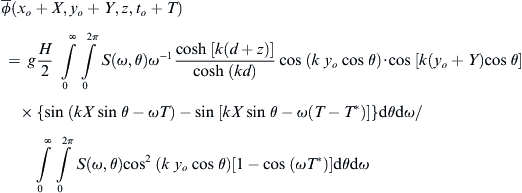 (11.3)
(11.3)
 (11.4)
(11.4)
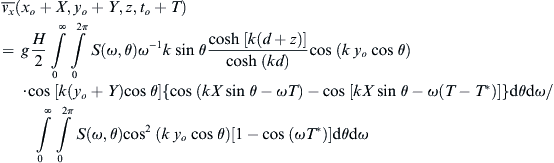 (11.5)
(11.5)
 (11.6)
(11.6)
 (11.7)
(11.7)
 (11.8)
(11.8)
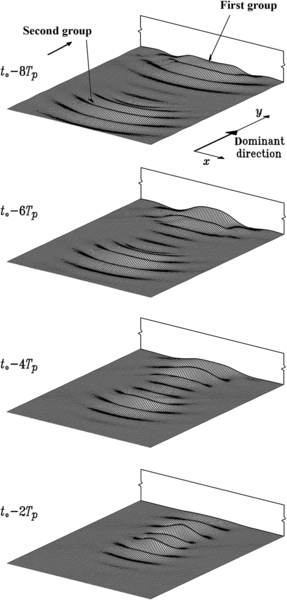
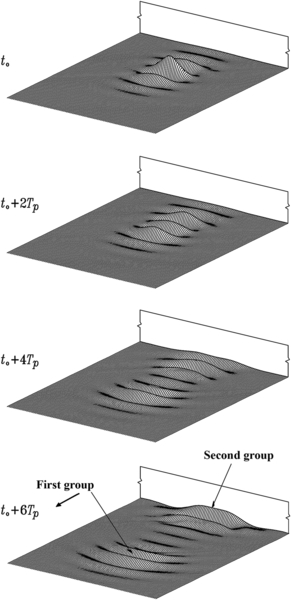
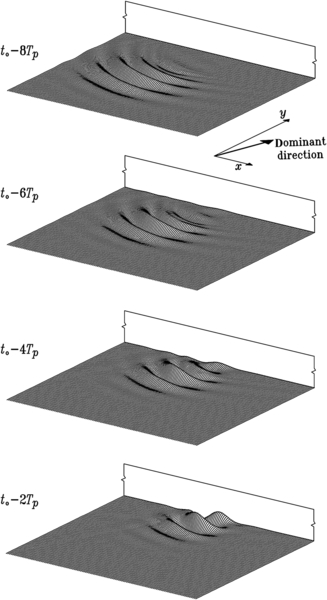
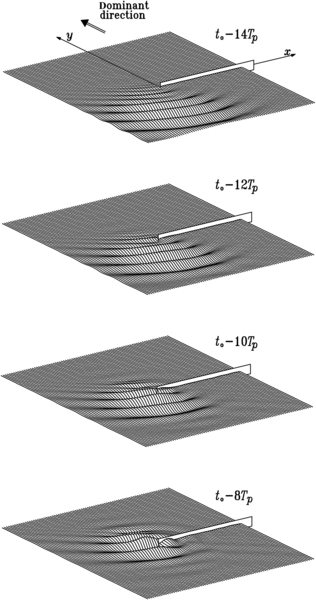
11.1.2. Occurrence of Exceptionally Large Waves before an Upright Breakwater


11.1.3. Wave Loads on Structures

![]() (11.9)
(11.9)
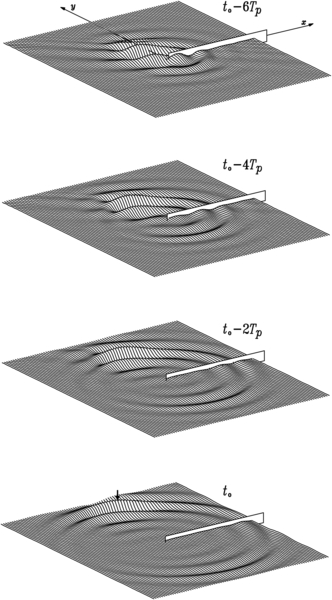
11.2. In the Lee of a Breakwater
11.2.1. Equations of Deterministic Waves in the Lee of a Breakwater
 (11.10)
(11.10)
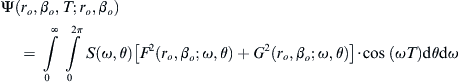 (11.11)
(11.11)
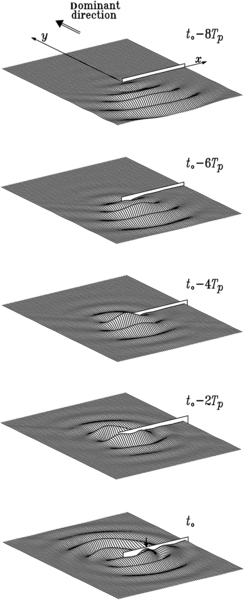
11.2.2. Occurrence of Exceptionally Large Waves in the Lee of a Breakwater
![]()
![]()
11.3. Experimental Verification

11.4. Conclusion

