CHAPTER 11

A Second Construction of Autodual Objects

In this construction, we work on the split form G_m/k, Spec(k[x, 1/x]). We begin with a geometrically irreducible lisse sheaf F on an open dense set U ⊂ G_m which is ι-pure of weight zero and which is self-dual: F ≅ F.

Denote by d the rank of F. We view F |U as a d-dimensional representation ρ of (U), toward either the orthogonal group O(d)/Q_ℓ, if the autoduality is orthogonal, or toward the symplectic group Sp(d)/Q_ℓ if the autoduality is symplectic (which forces d to be even). We denote by G_geom,F the Zariski closure of the image ρ((U)) of the geometric fundamental group.¹

We have a finite morphism

π : G_m[1/(x² + 1)] → G_m, x x + 1/x.

Then π^?F is lisse and ι-pure of weight zero on some open set j : V ⊂ G_m.

Theorem 11.1. For F as above, consider the middle extension sheaf G := j_?π^?F on G_m/k. Suppose in addition the following three conditions hold.

(1) If d = 1, G is not geometrically a Kummer sheaf L_χ.

(2) If the autoduality of F is orthogonal, then d ≠ 2 and G_geom,_F is either O(d) or SO(d).

(3) If the autoduality of F is symplectic, G_geom,F is Sp(d).

Then N := G (1/2)[1] lies in P_arith and is ι-pure of weight zero. It is geometrically irreducible and arithmetically self-dual. The sign of its autoduality is opposite to that of F.

Proof. The lisse sheaf F on U is geometrically Lie-irreducible, because G⁰_geom,_F, which is either SO(d), d ≠ 2, or Sp(d), acts irreducibly in its standard representation. Therefore π^?F, or indeed any pullback of F by a finite morphism, remains geometrically Lie-irreducible. Thus N is perverse, ι-pure of weight zero., and geometrically irreducible, so by (1) is a geometrically irreducible object of P_arith. It is arithmetically self-dual, because isomorphic to both its Verdier dual (thanks to the autoduality of F) and to its pullback by multiplicative inversion (thanks to having been pulled back by π). It remains to determine the sign ²_N of its autoduality.

The idea is quite simple. Let us denote by ²_F the sign of the auto-duality of F. Then ²_F is the large #E limit of the sums

cf. [Ka-GKM, 4.2]. On the other hand, ²_N is the large #E limit of the sums

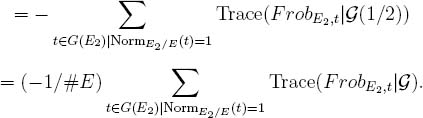
Now for any t ∈ G(E₂) with t² + 1 ≠ 0 and such that t + 1/t lies in U, we have

Trace(Frob_{E2, t}|G) = Trace(Frob_{E2, t+ 1/t}|F).

So ²_N is the large #E limit of the sums

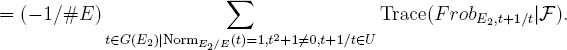
For t ∈ G(E₂) with Norm_E2/E(t) = 1, t + 1/t is just Trace(t). With the exception of the points ±1, every point t ∈ G(E₂) with Norm_E2/E(t) = 1 has degree two over E, so is a root of a quadratic polynomial T² – sT + 1 ∈ E[T ]. Here s = t + 1/t. Conversely, an irreducible quadratic polynomial of the form T² – sT + 1 ∈ E[T ] has two roots, t and 1/t in G(E₂) with Norm_E2/E(t) = Norm_E2/E(1/t) = 1, t+ 1/t = s. In other words, the set of t ∈ G(E₂) with Norm_E2/E(t) = 1, t ≠ ±1, is a double covering, by t t + 1/t = Trace(t), of the set of s ∈ E such that the quadratic polynomial T² – sT + 1 is E-irreducible. Thus this last sum is within O(1#E) of the sum

We will show that the sums whose large #E limit is ²_F, namely

are within O(1/√#E) of the sums

whose large #E limit is – ²_N.

We first treat the case when k has odd characteristic. Shrinking U if necessary, we may suppose that neither 2 nor –2 lies in U. Now T² – sT + 1 is E-irreducible if and only if its discriminant s² – 4 is a nonzero nonsquare in E. Denoting by χ_{2, E} the quadratic character of E^×, we then have, for s ∈ U(E),

1 – χ_{2, E}(s² – 4) = 0

if s² – 4 is a square, and

1 – χ_{2, E}(s² – 4) = 2

if s² – 4 is a nonsquare.

So the sums whose large #E limit is – ²_N are

Hence we are reduced to showing that the sums

are O(1/√#E). To see this, we make use of the linear algebra identity Trace(Frob_E2,s|F) = Trace(Frob_E,s|Sym²(F))–Trace(Frob_E,s|Λ²(F)). So it suffices to prove that both of the sums

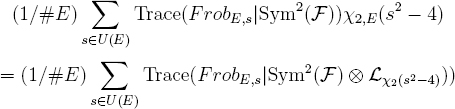
and

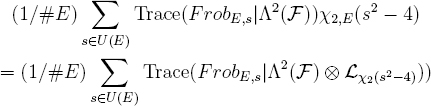
are O(1/√#E).

If the arithmetic autoduality of F has G_geom,F = Sp(d), then Sym²(F) is (both arithmetically and) geometrically irreducible, and it has rank > 1. Therefore its tensor product with any lisse rank one sheaf, here L_χ2(s^2–4), remains (both arithmetically and) geometrically irreducible. Therefore its H²_c(U/k, Sym²(F) ⊗L_χ2(s2–4))) vanishes. Because F is ι-pure of weight zero, so is Sym²(F) ⊗L_χ2(s2–4), and hence by Deligne [De-Weil II, 3.3.1] its H¹_c is ι-mixed of weight ≤ 1. By the Lefschetz Trace formula [Gr-Rat] and the vanishing of the H²_c,

= –(1/#E)Trace(Frob_E|H¹_c(U/k, Sym²(F) ⊗L_χ2(s2–4)))

is O(1/√#E). And the sheaf Λ²(F) is either the constant sheaf Q_ℓ if d = 2 or, if d ≥ 4, the direct sum

Λ²(F) = Q_ℓ ⊕H,

with H an arithmetically and geometrically irreducible lisse sheaf of rank > 1. Again H⊗L_χ2(s²–4) is ι-pure of weight zero and has vanishing H²_c, and an H¹_c which is ι-mixed of weight ≤ 1. So the sum

is O(1/√#E). The final term is

which again is O(1/√#E) because L_χ2(s²–4) is geometrically nontrivial.

If the arithmetic autoduality of F has G_geom,F containing SO(d) with d ≠ 2, we argue as follows. We first treat separately the case d = 1. Then F is a lisse sheaf of rank one whose trace function takes values in ±1. Therefore Λ²(F) = 0, and Sym²(F) = F^⊗2 is the constant sheaf. So the sum we must estimate is just

which as noted above is O(1/√#E).

If d ≥ 3, the argument is essentially identical to the argument in the symplectic case, except that now it is Λ²(F) which is arithmetically and geometrically irreducible of rank > 1, and it is Sym²(F) which admits a direct sum decomposition

Sym²(F) = Q_ℓ ⊕H,

with H an arithmetically and geometrically irreducible lisse sheaf of rank > 1.

It remains to treat the case of characteristic 2, where we no longer have the discriminant to tell us when T² – sT + 1 is E-irreducible. In characteristic 2 we consider directly the finite étale covering of G_m by G_m {1} given by π : t t + 1/t := s. This extends to a finite étale covering of P¹ {0} by P¹ {1}. Making the change of variable t = u/(u + 1), we readily compute

1/s = 1/(t + 1/t) = 1/(u/(u + 1)+ (u + 1)/u) = u² – u.

Thus in characteristic two, the role of L_χ2(s2–4) is now played by the Artin-Schreier sheaf L_Ã(1/s). With this change, we just repeat the proof from odd characteristic.

Here is a slight generalization of the previous result, where we relax the hypotheses on the group G_geom,F attached to the geometrically irreducible lisse sheaf F on an open dense set U ⊂ G_m which is ι-pure of weight zero and which is self-dual: F ≅ F. We make the following two hypotheses.

(1) The identity component G⁰_geom,F acts irreducibly in its given d-dimensional representation ρ.

(2) In the representation ρ⊗ρ corresponding to F⊗F, thespaceof invariants under G_geom,F is one-dimensional, and every other irreducible constituent of ρ ⊗ ρ for the action of G_geom,F has dimension > 1.

These conditions are automatically satisfied in the symplectic case when G_geom,F = Sp(d), and in the orthogonal case when d ≠ 2 and G_geom,F contains SO(d). But they are also satisfied if G_geom,F receives an SL(2) such that ρ|SL(2) is irreducible. For then ρ|SL(2) must be Sym^d–1(std₂) as SL(2)-representation, and one knows that

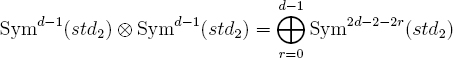
as SL(2)-representation. For later use, let us recall that in the world of GL(2)-representations, we have

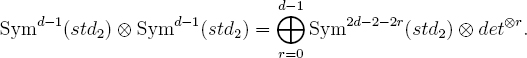
In fact, one has the more precise decompositions

and

Theorem 11.2. For F as above, satisfying the hypotheses (1) and (2), consider the middle extension sheaf G := j_V?π^?F on G_m/k. Then N := G(1/2)[1] lies in P_arith and is ι-pure of weight zero. It is geometrically irreducible and arithmetically self-dual. The sign of its autoduality is opposite to that of F.

Proof. Repeat the proof of Theorem 11.1. In the symplectic case, Λ²(F) has an invariant corresponding to the symplectic form, so we have a direct sum decomposition Λ²(F) = H⊕ Q_ℓ. By hypothesis (2), each G_geom,F -irreducible constituent of H has dimension ≥ 2, and each G_geom,F -irreducible constituent of Sym²(F)has dimension ≥ 2. These conditions ensure the vanishings of the various H²_c in the proof. In the orthogonal case, reverse the roles of Sym² and Λ².

¹See the notational caution at the very end of the Introduction.