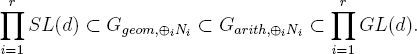CHAPTER 13

Results of Goursat-Kolchin-Ribet Type

Suppose we are given some number r ≥ 2 of objects N₁, N₂, …, N_r in P_arith of some common “dimension” d ≥ 1. Suppose they are all ι-pure of weight zero, geometrically irreducible, and arithmetically self-dual, all with the same sign of duality.

Theorem 13.1. Suppose that d ≥ 2 is even, that each N_i is symplectically self-dual, and that for each i = 1, …, r, we have G_geom,Ni = G_arith,Ni = Sp(d). Suppose further that for i ≠ j, there is no geometric isomorphism between N_i and N_j and there is no geometric isomorphism between N_i and [x –x]^? N_j. Then the direct sum ⊕_iN_i has

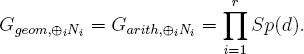
Proof. We apply the Goursat-Kolchin-Ribet theorem [Ka-ESDE, 1.8.2] to the group G_geom,⊕iNi and its representations V_i corresponding to the N_i. In order to show that G_geom,⊕iNi = Π_i Sp(d), it suffices to show that for i ≠ j, there is no geometric isomorphism between N_i and N_j ?_mid L, for any one-dimensional object L of <⊕_iN_i>_geom. In fact, we will show that, under the hypotheses of the theorem, there is none for any one-dimensional object of P_geom. Suppose there were. Both N_j and N_j ?_mid L ≅ N_i are symplectic representations, with image Sp(d). But the only scalars in Sp(d) are ±1. Therefore L^⊗2 in the Tannakian sense, i.e., L ?_mid L, is geometrically trivial. One knows [Ka-ESDE, 8.5.3] that the only one-dimensional objects in P_geom are delta objects δ_a for some a ∈ k^× and multiplicative translates of hypergeometric sheaves placed in degree –1. But such hypergeometric objects are of infinite order, as middle self-convolution simply produces other such objects, of larger and larger generic rank. Therefore our L must be some δ_a. Because L ?_mid L is geometrically trivial, we conclude that a = ±1. But middle convolution with δ_a is just multiplicative translation by a. Therefore we have G_geom,⊕iNi = Π_i Sp(d). Since in any case we have G_geom,⊕iNi ⊂ G_arith,⊕iNi ⊂ Π_i Sp(d), we get the asserted equality

Theorem 13.2. Suppose that d ≥ 6 is even, d ≠ 8, that each N_i is orthogonally self-dual, and that for each i = 1, …, r, we have G_geom,Ni = SO(d). Suppose further that for i ≠ j, there is no geometric isomorphism between N_i and N_j and there is no geometric isomorphism between N_i and [x –x]^? N_j. Then the direct sum ⊕_iN_i has

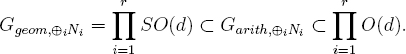
If in addition we have G_geom,Ni = G_arith,Ni = SO(d) for every i, then

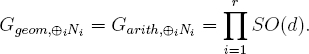
Proof. The proof, via the Goursat-Kolchin-Ribet theorem [Ka-ESDE, 1.8.2], is identical to the previous one.

Theorem 13.3. Suppose that d ≥ 3 is odd, that each N_i is orthogonally self-dual, and that for each i = 1, …, r, we have G_geom,Ni = SO(d). Suppose further that for i ≠ j, there is no geometric isomorphism between N_i and N_j. Then the direct sum ⊕_iN_i has

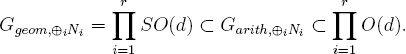
If in addition we have G_geom,Ni = G_arith,Ni = SO(d) for every i, then

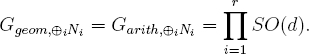
Proof. The proof, again via the Goursat-Kolchin-Ribet theorem [Ka-ESDE, 1.8.2] is even simpler in this case, because for d odd, SO(d) contains no scalars other than 1, so L can only be δ₁.

In the orthogonal case, the Goursat-Kolchin-Ribet theorem [Ka-ESDE, 1.8.2] gives the following less precise version of these last two theorems.

Theorem 13.4. Suppose that either d ≥ 6 is even, d ≠ 8, or d ≥ 3 is odd. Suppose that each N_i is orthogonally self-dual, and that for each i = 1, …, r, we have SO(d) ⊂ G_geom,Ni. Suppose further that for i ≠ j, there is no geometric isomorphism between N_i and N_j and there is no geometric isomorphism between N_i and [x –x]^? N_j. Then the direct sum ⊕_iN_i has

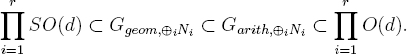
We end this chapter with the case of SL(d).

Theorem 13.5. Suppose that for each i = 1, …, r, we have SL(d) ⊂ G_geom,Ni. Denote by N^∨_i the dual in the Tannakian sense of N_i. Suppose further that for every one-dimensional object L ∈ P_geom, and for i ≠ j, there is no geometric isomorphism between N_i and N_j ?_midL nor between N_i and N^∨_j ?_mid L. Then the direct sum ⊕_iN_i has