CHAPTER 19

Orthogonal Examples, Especially SO(n) Examples

The orthogonal case is more difficult than the symplectic one because of the need to distinguish between SO(n) and O(n), which we do not in general know how to do. We work on either the split or the nonsplit form. We begin with a lisse sheaf F on a dense open set j : U ⊂ G which is geometrically irreducible, pure of weight zero, and not geometrically isomorphic to (the restriction to U of) any Kummer sheaf L_χ. We denote by G := j_? F its middle extension to G. Then the object N := G(1/2)[1] ∈ P_arith is pure of weight zero and geometrically irreducible. The following result is the orthogonal version of Theorem 18.1.

Theorem 19.1. Suppose that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself, and that N is orthogonally self-dual. Suppose further that for either of the two possible geometric isomorphisms G/k ≅ G_m/k, both F(0)^unip and F(∞)^unip are single Jordan blocks Unip(e) of the same size e ≥ 1. For n := dim(!(N)) we have

SO(n) ⊂ G_geom,N ⊂ G_arith,N ⊂ O(n).

Proof. The proof is nearly identical to that of Theorem 18.1. We have a priori inclusions

G_geom,N ⊂ G_arith,N ⊂ O(n),

so it suffices to prove that G⁰_{geom, N} = SO(n). We may extend scalars if necessary from k to its quadratic extension k₂, and reduce to the case where G is G_m. The hypothesis that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself insures that N is geometrically Lie-irreducible, i.e., that G⁰_geom is an irreducible connected subgroup of SO(n). Thus G⁰_geom is semisimple, cf. the proof of Theorem 18.1.

The local monodromy of N at both 0 and ∞ is Unip(e). Therefore the semisimplification of Frob_k, gives us a Frobenius torus Diag(x, 1/x, 1, …, 1) in G_arith,N. This torus normalizes the connected semisimple group G⁰_{geom, N}. Exactly as in the symplectic case, it follows that G⁰_{geom, N} contains the torus Diag(x, 1/x, 1, …, 1). By the result of Kostant and Zarhin [Ka-ESDE, 1.2], the only irreducible connected semisimple subgroups of SL(n)which contain Diag(x, 1/x, 1, …, 1) are SL(n), SO(n), and, when n is even, Sp(n). Since we have an a priori inclusion G⁰_{geom, N} ⊂ SO(n), we must have G⁰_{geom, N} = SO(n).

Here is the orthogonal analogue of Theorem 18.2. Its proof, via Goursat-Kolchin-Ribet [Ka-ESDE, 1.8.2] and Theorems 13.2, 13.3 and 13.4, is entirely analogous.

Theorem 19.2. Suppose N satisfies all the hypotheses of the theorem above. Suppose further that

(a) Either n ≥ 3 is odd, or n ≥ 6, n ≠ 8, is even.

(b) At either 0 or at ∞ or at both, the entire tame part of the local monodromy is Unip(e), i.e., local monodromy there is the direct sum of Unip(e) and of something totally wild.

Given s ≥ 2 distinct characters χ₁, …, χ_s of G(k), form N_i := N ⊗ L_χi. Denote by (^s_i=1 O(n))_{=det′ s} the subgroup of ^s_i=1 O(n) consisting of those elements whose determinants are either all 1 or all –1. We have the following conclusions.

(1) If G_geom,N = G_arith,N = SO(n), then

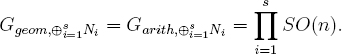
(2) If G_geom,N = SO(n) and G_arith,N = O(n), then

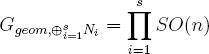
and

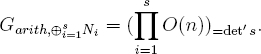
(3) If G_geom,N = G_arith,N = O(n), and if χ_i(–1) = 1 for all i, then

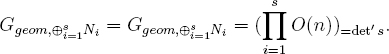
Proof. As already noted, M M ⊗ L_χi is a Tannakian isomorphism of <N>_arith with <N ⊗ L_χi>_arith. In particular, the determinants in the Tannakian sense are related by “det” (N ⊗ L_χi) = “det” (N)⊗L_χi. But “det” (N) is either δ₁ (case (1)) or (–1)^deg ⊗ δ₁ (case (2)) or δ_–1 or (–1)^deg ⊗ δ_–1 (case (3)), each of which is unchanged when we tensor it with any Lχ_i, so long as, in case (3), χ_i(–1) = 1. Case (1) is immediate from the previous result. In case (2), the previous result gives G_geom, ⊕^s_i=1^N_i = ^s_i=1 SO(n). We get the asserted value for G_{arith,⊕^si=1}^N_i by observing that it must strictly contain ^s_i=1 SO(n) but lies in (^s_i=1 O(n)_=det′ s. In case (3), we get the asserted value for G_geom, ⊕^s_i=1^N_i by observing that by the previous result it contains ^s_i=1 SO(n) then that it must strictly contain ^s_i=1 SO(n) and finally that it lies in ^s_i=1 O(n)_{=det′ s}. Then G_{arith,⊕^si=1}^N_i contains (^s_i=1 O(n)_=det′ but also is contained in it.

We now turn to the construction of examples in which G_geom,N = SO(n). Let us first explain the method we will use to show that G_geom,N is SO(n) rather than O(n). Given a finite subgroup Γ ⊂ G(k), we say that an object N ∈ P_geom is adapted to Γ if its restriction to the complement of Γ is lisse, i.e., if N|(G Γ) is a lisse sheaf placed in degree –1. In general it is not true that the middle convolution of two objects adapted to Γ is again adapted to Γ. Here is a simple example. Whatever the choice of Γ, any N ∈ P_geom which is lisse on G is adapted to Γ. For example, take Γ = {1}, and the Artin-Schreier objects L_Ã(x)(1/2)[1] and L_Ã(–a/x)(1/2)[1]. Their middle convolution is δ_a, which is not adapted to this Γ unless a = 1. We do, however, have the following lemma.

Lemma 19.3. Suppose Γ ⊂ G(k) is a finite subgroup, and N ∈ P_geom is adapted to Γ and geometrically semisimple. Suppose further that the local monodromy of N at both 0 and ∞ is tame. Then every object in <N>_geom is adapted to Γ.

Proof. Every object in <N>_geom is a direct summand of a multiple middle convolution of N and its dual [x 1/x] ^? DN, both of which are adapted to Γ and tame at both 0 and ∞. Proceeding by induction on the number of multiple convolutions, we reduce to the following lemma.

Lemma 19.4. Suppose Γ ⊂ G(k) is a finite subgroup, and N and M in P_geom are adapted to Γ and geometrically semisimple. Suppose further that the local monodromy of N at both 0 and ∞ is tame. Then the middle convolution N _?mid M is adapted to Γ.

Proof. We reduce immediately to the case when by N and M are geometrically irreducible. If either is punctual, it is δ_° for some element ° ∈ Γ. Then middle convolution with it is multiplicative translation by °, which preserves being adapted to Γ. So it suffices to treat the case where N = F[1] and M = G[1] are each middle extension sheaves placed in degree –1, both adapted to Γ, and where F is tame at both 0 and ∞. The conditions of being lisse outside Γ, and of being tame at both 0 and ∞, are each stable by Verdier duality. So it suffices to show that the ! convolution N ?_! M is lisse outside Γ. For if this is so, then the same statement applied to their Verdier duals DN and DM, shows that DN ?_! DM is lisse outside Γ, and so its Verdier dual D(DN ?_! DM) ≅ N ?_? M is also adapted to Γ. As the middle convolution N ?_mid M is the image of N _?! M in N?_? M, it too is lisse outside of Γ.

In order to show that N?_! M is lisse outside of Γ, we apply Deligne’s semicontinuity theorem [Lau-SCCS, 2.1.2]. For a ∈ G Γ, the sheaf

H := F ⊗ [x a/x] ^? G

is lisse outside the 2#Γ points of Γ ∪ aΓ^–1. By Deligne’s theorem, it suffices to show that in the formula for its Euler characteristic,

each term is independent of the choice of a, so long as a is not in Γ. Because F is tame at 0, we have Swan₀(H) = rank(F)Swan_∞(G). Because F is tame at ∞, we have Swan_∞(H) = rank(F)Swan₀(G). At apoint ° ∈ Γ, we have drop_°(H) = drop_°(F)rank(G)and Swan_°(H) = Swan_°(F)rank(G). At a point a/° ∈ aΓ^–1, we have drop_a/°(H) = rank(F)drop_°(G) and Swan_a/°(H) = rank(F)Swan_°(G).

Here is a variant, with the same proof.

Lemma 19.5. Suppose S, T ⊂ G(k) are finite nonempty subsets, and N ∈ P_geom is lisse outside S and geometrically semisimple. Suppose further that the local monodromy of N at both 0 and ∞ is tame. Suppose M ∈ P_geom is lisse outside T, and geometrically semisimple. Then their middle convolution N ?_mid M is lisse outside ST := {st, s ∈ S, t ∈ T }.

Here is yet another variant, with the same proof.

Lemma 19.6. Suppose S ⊂ G(k) is a finite nonempty subset, and N ∈ P_geom is lisse outside S and geometrically semisimple. Suppose further that the local monodromy of N at both 0 and ∞ is tame. Suppose M ∈ P_geom is lisse on G_m (so M is F[1] for a lisse sheaf F on G_m). Then their middle convolution N ?_mid M is lisse on G_m.

We can apply these results as follows.

Theorem 19.7. Let Γ ⊂ G(k) be a finite subgroup. Suppose that 1 is the only element of order dividing 2 in Γ. This condition is automatic in characteristic 2; in odd characteristic it is the condition that –1 not be in Γ. Let F be a lisse sheaf on G Γ which is geometrically irreducible, pure of weight zero, and not geometrically isomorphic to (the restriction to G Γ of) any Kummer sheaf L_χ. We denote by G := j_?F its middle extension to G, and by N the object N := G(1/2)[1] ∈ P_arith, which is pure of weight zero and geometrically irreducible. Suppose N is orthogonally self-dual. Suppose that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Suppose further that for either of the two possible geometric isomorphisms G/k ≅ G_m/k, F is tame at both 0 and ∞, and both F(0)^unip and F(∞)^unip are single Jordan blocks Unip(e) of the same size e ≥ 1. For n := dim(!(N)) we have

G_geom,N = SO(n).

Moreover, either G_arith,N = SO(n), or “det”(N) in the Tannakian sense is arithmetically (–1)^deg ⊗ δ₁, i.e., for any finite extension field E/k and any character ρ of G(E), det(Frob_E,ρ) = (–1)^deg(E/k).

Proof. By Theorem 19.1, we know that G_geom,N is either SO(n) or O(n). So it suffices to show that “det”(N) in the Tannakian sense is geometrically trivial. It is a one-dimensional object of <N>_geom which has order two, so in odd characteristic it is either δ₁ or δ_–1. [In characteristic 2 it can only be δ₁, and we are done.] By Lemma 19.3, “det”(N) is adapted to Γ. If –1 is not in Γ, “det”(N) cannot be δ_–1, so geometrically it must be δ₁. So arithmetically it must be α^deg ⊗ δ₁, with α = ±1.

Here is a variant.

Theorem 19.8. Let S ⊂ G(k) be a finite nonempty subset. For each integer d ≥ 1, denote by S^d ⊂ G(k) the set of all d-fold products of elements of S. Let F be a lisse sheaf on GS which is geometrically irreducible, pure of weight zero, and not geometrically isomorphic to (the restriction to G Γ of) any Kummer sheaf L_χ. We denote by G := j_?F its middle extension to G, and by N the object N := G(1/2)[1] ∈ P_arith, which is pure of weight zero and geometrically irreducible. Suppose N is orthogonally self-dual. Suppose that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Suppose further that for either of the two possible geometric isomorphisms G/k ≅ G_m/k, F is tame at both 0 and ∞, and both F(0)^unip and F(∞)^unip are single Jordan blocks Unip(e) of the same size e ≥ 1. Suppose further that for n := dim(!(N)) the “dimension” of N, the set Sⁿ does not contain –1. Then

G_geom,N = SO(n).

Moreover, either G_arith,N = SO(n), or “det”(N) in the Tannakian sense is arithmetically (–1)^deg ⊗ δ₁, i.e., for any finite extension field E/k and any character ρ of G(E), det(Frob_E,ρ) = (–1)^deg(E/k).

Proof. The determinant, in the Tannakian sense, of N is a summand of the n-fold middle convolution of N with itself, so by Lemma 19.5 it is lisse outside Sⁿ. Therefore it cannot be δ_–1, and we conclude as in the proof of the previous theorem.

We now give some examples. For the first example, we work in odd characteristic. We begin with an irreducible hypergeometric sheaf H of type (2m, 2n) with 2m < 2n, of the form

H(Ã; χ₁, …, χ_2m; , , …., )((2m + 2n – 1)/2)

which is symplectically self-dual. Its local monodromy at ∞ is Unip(2n), cf. [Ka-ESDE, 8.4.11]. Given that all the characters at ∞ are imposed to be trivial, the geometric irreducibility means that no χ_i is trivial, and the symplectic autoduality then means that an even number 2r ≥ 0 of them are the quadratic character, and that the remaining ones, if any, occur in complex conjugate pairs, cf. [Ka-ESDE, 8.8.1, 8.8.2]. One knows its geometric monodromy group is Sp(2n), cf. [Ka-GKM, 11.6].

Theorem 19.9. Starting with H as above, in which 2r quadratic characters occur, form the lisse sheaf G := [x x–2+ 1/x] ^?H on G_m{1}, then form the object N := j_1?G(1/2)[1] ∈ P_arith, which is pure of weight zero. Then N is orthogonally self-dual, and we have the following results.

(1) If 2r = 0, then “dim”(N) = 2n + 2, and G_geom,N = SO(2n + 2).

(2) If 2r > 0, then “dim”(N) = 2n + 1, and G_geom,N = SO(2n + 1).

Proof. The pullback G has local monodromy Unip(2n) at both 0 and ∞. To analyze its local monodromy at 1, observe that the map x x + 1/x – 2 is doubly ramified over 0, with 1 as the unique point lying over. So the local monodromy of G at 1 is the direct sum of three pieces: Unip(2r), a tame part of rank 2m – 2r with no nonzero inertial invariants, and a totally wild part of rank 2n–2m and Swan conductor 2. So the “dimension” of N is drop₁ + Swan₁.

If 2r = 0, then drop₁ = 2n, otherwise drop₁ = 2n – 1. Thus the “dimension” is as asserted. By Theorem 11.1, N is orthogonally self-dual. Because 1 is the only singularity of N in G_m, N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. The result now follows from the Γ = {1} case of Theorem 19.7.

In the next example, in odd characteristic p ≠ 5, we begin with an odd symmetric power of TwLeg, say F := Sym^2d–1 (TwLeg)(d). This is a lisse sheaf on G_m {1} which is pure of weight zero, symplectically self-dual, and has geometric monodromy SL(2), acting in Sym^2d–1(std₂). Its local monodromies at 0 and ∞ are both Unip(2d). Its local monodromy at 1 is L_χ2 ⊗ Unip(2d). We form its pullback G := [x x + 1/x – 2]^? F, which is lisse on the open set j : G_m {1, (3 ± √5)/2} ⊂ G_m. Its local monodromy at 1 is Unip(2d). Its local monodromy at each of the points (3 ± √5)/2 is L_χ2 ⊗ Unip(2d). We then form

N := j_?G(1/2)[1],

which is pure of weight zero and of “dimension” drop₁ + drop_{(3+ √5)/2} + drop_(3–√5)/2 = 2d–1+ 2d+ 2d = 6d–1. By Theorem 11.1, N is orthogonally self-dual. Because 1 is the unique singularity in G_m at which the local monodromy is unipotent, N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. By Theorem 19.1, we have SO(6d – 1) ⊂ G_geom,N.

We wish to apply Theorem 19.8. Here the set S in F_p^× (remember p ≠ 2, 5) is the three element set {1, (3 + √5)/2, (3 – √5)/2}. Notice that (3 + √5)/2 is a totally positive unit in the ring of integers of Q(√5), whose inverse is the totally positive unit (3–√5)/2. This total positivity shows that in Q(√5)^×, the multiplicative subgroup generated by (3+ √5)/2 does not contain –1. It follows that in large characteristic p, the set S^6d–1 does not contain –1.

To make this precise, let us fix a totally positive unit u ≠ 1 in the ring of integers O_K of a real quadratic field K. We define a sequence of strictly positive integers¹ N(u, n), n ≥ 1, by

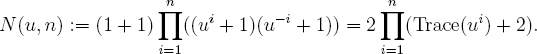
Notice that N(u, n + 1) = (Trace(u^{n+ 1})+ 2)N(u, n), so the N(u, n) successively divide each other. For our S = {1, (3+ √5)/2, (3–√5)/2}, Sⁿ is the set {uⁱ, –n ≤ i ≤ n} for u = (3 + √5)/2. So we get the following theorem.

Theorem 19.10. Let p be a prime which does not divide the integer N((3 + √5)/2, 6d – 1). Then N as above, formed out of the pullback of Sym^2d–1(TwLeg)(d) by x x + 1/x – 2, has G_geom,N = SO(6d – 1).

Remark 19.11. We do not know if the restriction on p in the above theorem is in fact necessary. For example, starting with Sym¹(TwLeg), i.e., d = 1, we are omitting primes dividing N((3 + √5)/2, 5) = 11025000 = 2²3²5⁵7². Are the omissions of 3 and 7 needed? We also do not know whether or not we also have G_arith,N = SO(6d – 1) for the “good” primes p. These same problems persist for the next example as well.

Here is another example, still in odd characteristic, this time based on pulling back a hypergeometric sheaf H of type (2n, 2n) which is symplectically self-dual. We assume H is of the form

H(Ã; χ₁, …, χ_2n; , ,.., )((4n – 1)/2),

with no χ_i trivial, with an even number 2r of the χ_i the quadratic character, and with the remaining ones, if any, occurring in complex conjugate pairs.

Theorem 19.12. Starting with H as above, in which 2r quadratic characters occur, form the lisse sheaf G := [x x + 1/x – 2]^?H on G_m {1, (3 ± √5)/2}, then form the object N := j_?G(1/2)[1] ∈ P_arith, which is pure of weight zero. Then N is orthogonally self-dual, and we have the following results.

(1) If 2r = 0, then “dim”(N) = 2n + 2, and SO(2n + 2) ⊂ G_geom,N. If p := char(k) does not divide N((3+ √5)/2, 2n+ 2), then G_geom,N = SO(2n + 2).

(2) If 2r > 0, then “dim”(N) = 2n + 1, and SO(2n + 1) ⊂ G_geom,N. If p := char(k) does not divide N((3+ √5)/2, 2n+ 1), then G_geom,N = SO(2n + 1).

Proof. The pullback G has local monodromy Unip(2n) at both 0 and ∞. To analyze its local monodromy at 1, observe that the map x x + 1/x – 2 is doubly ramified over 0, with 1 as the unique point lying over. So the local monodromy of G at 1 is the direct sum of two (or one, if 2r = 0) pieces: Unip(2r), and a tame part of rank 2n – 2r with no nonzero inertial invariants. At each of the two points (3 ± √5)/2, which map to 1, the local monodromy is a unipotent pseudoreflection. So the “dimension” of N is drop₁ + drop_(3+√5)/2 + drop_(3–√5)/2. The first term, drop₁, is 2n if 2r = 0, otherwise it is 2n – 1. At each of the two points (3 ± √5)/2, the drop is 1. So the dimension is as asserted. By Theorem 11.1, N is orthogonally self-dual. Because 1 is the unique singularity in G_m at which the local monodromy is not a unipotent pseudoreflection, N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. So by Theorem 19.1, G_geom,N contains the group SO(2n + 1) when 2r > 0, respectively the group SO(2n + 2) when 2r = 0. To get the more precise statement, we apply Theorem 19.8. Here the set S is again the three element set {1, (3 + √5)/2, (3 – √5)/2}. If the characteristic p does not divide the integer N((3 + √5)/2, 2n + 1) when 2r > 0, respectively the integer N((3 + √5)/2, 2n + 2) when 2r > 0, then S^{2n+ 1}, respectively S^{2n+ 2} does not contain –1.

Remark 19.13. Whenever we have an N for which we know that G_geom,N = SO(n) and we know that G_arith,N ⊂ O(n), then either G_arith,N = SO(n), or G_arith,N = O(n). In the latter case, “det”(N) is geometrically trivial, and of order two, so necessarily (–1)^deg. The problem is that in general we don’t know which situation we are in. But in both cases, if we extend scalars from the given ground field k to its quadratic extension, we achieve a situation in which G_geom = G_arith = SO(n).

¹The interest of these integers N(u, n) is this. If a prime p does not divide N(u, n), then for any field k of characteristic p, and for any ring homomorphism φ : O_K → k, none of the elements φ(uⁱ), for –n ≤ i ≤ n, is equal to –1 in k: if p divides N(u, n), then for every such φ at least one of the elements φ(uⁱ), –n ≤ i ≤ n, is equal to –1 in k.