CHAPTER 25

G₂ Examples: the Overall Strategy

In this and the next two chapters, we fix, for each prime p, a prime ℓ ≠ p and a choice of nontrivial Q_ℓ^×-valued additive character à of the prime field F_p. Given a finite extension field k/F_p, we take as nontrivial additive character of k the composition Ã_k := à ◦ Tr_k/Fp, whenever a nontrivial additive character of k is (implicitly or explicitly) called for (for instance in the definition of a Kloosterman sheaf, or of a hypergeometric sheaf, on G_m/k). Given a finite field k of characteristic p, and a (possibly trivial) multiplicative character χ of k^× which, if p is odd, is not the quadratic character χ₂, we form the following lisse sheaf F(χ, k)on G_m/k. If p = 2, we take the Tate-twisted Kloosterman sheaf of rank seven

F(χ, k) := Kl(, , , χ, χ, χ, χ)(3).

If p is odd, we take the “Gauss sum twisted” hypergeometric sheaf of type (7, 1)

F(χ, k) := (A^–7)^deg ⊗ H(, , , χ, χ, χ, χ; χ₂),

with A the negative of the quadratic Gauss sum:

It is proven in [Ka-G2Hyper, 9.1] that each of these lisse sheaves is pure of weight zero, orthogonally self-dual, and has G_geom = G_arith = G₂ (with G₂ seen as a subgroup of SO(7) via G₂’s irreducible seven-dimensional representation).

We think of this result in the following way: for #k large, and χ fixed, the semisimplifications of the #k^× Frobenius conjugacy classes {Frob_a,k|F(χ, k)}_a∈k^× attached to the lisse sheaf F(χ, k) at the points a ∈ k^× are approximately equidistributed in the space of conjugacy classes of the compact group UG₂, the compact form of G₂. What we would like to prove (but cannot, at present) is that, for #k large, if we fix a point a ∈ k^×, the semisimplifications of the (#k^×, if p = 2, #k^× – 1 if p is odd) Frobenius conjugacy classes {Frob_a,k|F(χ, k)}_χ indexed by the characters χ of k^× (with χ ≠ χ₂ when p is odd) are approximately equidistributed in the space of conjugacy classes of UG₂.

Recall that in UG₂, conjugacy classes are determined by their characteristic polynomials in the irreducible seven-dimensional representation. This holds because the two fundamental representations of G₂ are V_!1 = std₇, the irreducible seven-dimensional representation, and V_!2 = Lie(G₂), the adjoint representation. One knows that

Λ²(std₇) = std₇ ⊕ Lie(G₂),

and hence knowing the characteristic polyomial of an element of UG₂ determines its trace in both V_!1 = std₇ and V_!2 = Λ²(std₇) – std₇, and hence in every irreducible representation of UG₂. By Peter-Weyl, these traces determine the conjugacy class of the element.

Our main work will be to construct, for each finite field k and each element a ∈ k^×, an object N(a, k) ∈ P_arith on G_m/k with the following properties.

(1) (extension of scalars): Given a ∈ k^×, and a finite extension field E/k, the pullback of N(a, k) from G_m/k to G_m/E is the object N(a, E) on G_m/E constructed by viewing a as lying in E.

(2) N(a, k) is geometrically Lie-irreducible of “dimension” seven, pure of weight zero, and orthogonally self-dual. It has no bad characters.

(3) For any character χ of k^× (with χ ≠ χ₂ if p is odd), form the lisse sheaf F(χ, k) on G_m/k. Then we have the equality of characteristic polynomials

det(1 – TFrob_k,χ|!(N(a, k))) = det(1 – TFrob_a,k|F(χ, k)).

If we grant the existence of such objects N(a, k), we get the following theorem.

Theorem 25.1. Suppose we have objects N(a, k) as above. Then “with probability one,” N(a, k) has G_geom = G_arith = G₂. More precisely, in any sequence of finite fields k_i (possibly of different characteristics) with #k_i → ∞, the fractions

tend archimedeanly to 1.

Proof. We will prove this in a series of lemmas.

Lemma 25.2. Fix a finite field k of characteristic denoted p, and an element a ∈ k^×. We have the following results concerning the groups G_geom and G_arith for N(a, k) on G_m/k.

(1) We have G_geom = G_arith ⊂ SO(7).

(2) Either G_arith = G₂, or G_arith is the image of SL(2) in its irreducible representation V₇ := Sym⁶(std₂) of dimension seven.

Proof. Because N(a, k) is orthogonally self-dual, we have G_geom ⊂ G_arith ⊂ O(7). Thus “det” (N(a, k)) has order dividing 2, so is either δ₁ or (–1)^deg ⊗ δ₁, or, if p is odd, possibly δ_–1 or (–1)^deg ⊗ δ_–1.

We first show that “det” (N(a, k)) is δ₁. This will result from the identity

det(1 – TFrob_E,ρ|!(N(a, k))) = det(1 – TFrob_a,E|F(ρ, E)),

valid for every finite extension E/k and every character ρ of E^× (except χ₂, if p is odd), together with the fact that each such Frob_a,E|F(ρ, E) lies in G₂ ⊂ SO(7), so has determinant 1. Thus each such

det(Frob_E,ρ|!(N(a, k))) = 1.

If p = 2, and more generally if “det” (N(a, k)) is geometrically trivial, take E = k and ρ = to eliminate the (–1)^deg ⊗ δ₁ possibility. If p is odd, then over any sufficiently large extension field E of k (#E > 4 is big enough) there is a character ρ ≠ χ₂ with ρ(–1) = –1. Taking deg(E/k) to be of variable parity, the fact that det(Frob_{E, ρ}|!(N(a, k))) = 1 eliminates both the δ_–1 and (–1)^deg ⊗ δ_–1 possibilities. Thus we have G_geom ⊂ G_arith ⊂ SO(7).

Because N(a, k) is geometrically Lie-irreducible, the identity component G⁰_geom is an irreducible subgroup of SO(7). By Gabber’s theorem on prime-dimensional representations [Ka-ESDE, 1.6], the only irreducible connected subgroups of SO(7) are SO(7) itself, or G₂ in its seven-dimensional irreducible representation, or the image SL(2)/ ± 1 of SL(2) in V₇ := Sym⁶(std₂). Each of these groups is its own normalizer in SO(7) (because for each of these groups, every automorphism is inner, and the ambient group SO(7) contains no nontrivial scalars). Therefore G_arith, which lies in SO(7) and normalizes G_geom and consequently normalizes G⁰_geom, must be this same group. Thus we have

G⁰_geom = G_geom = G_arith,

and G_arith is either SO(7) or G₂ or the image SL(2)/ ± 1 of SL(2) in V₇ := Sym⁶(std₂).

Because N(a, k) in P_arith is geometrically (and hence arithmetically) irreducible, and pure of weight zero, the equality G_geom = G_arith implies (Theorem 1.1) the equidistribution of the Frobenius conjugacy classes in the space of conjugacy classes of a compact form K of G_arith. We now show that G_arith is not SO(7). We argue by contradiction. If G_arith were SO(7), then K would be SO(7, R) for the Euclidean inner product, its traces would fill the interval [–5, 7], and the set

{g ∈ K|Tr(g) < –4}

would be an open set of positive measure. Therefore for large extension fields E/k, there would exist, by equidistribution, characters ρ of E^× (with ρ ≠ χ₂ if p is odd) with Trace(Frob_{E, ρ}|!(N(a, k))) < –4. But we have Trace(Frob_{E, ρ}|!(N(a, k))) = Trace(Frob_a,E|F(ρ, E)). As noted above, Frob_a,E|F(ρ, E) has its semisimplification in UG₂, and one knows [Ka-NotesG2, 5.5] that the traces of elements of UG₂ in its seven-dimensional irreducible representation lie in the interval [–2, 7].

So the only two possibilities for G_arith are G₂ or the image of SL(2) in V₇ := Sym⁶(std₂). In the second case, K is the image of SU(2) in V₇ := Sym⁶(std₂).

We next give a property of the elements in the image of SL(2) in V₇ := Sym⁶(std₂) which can be used to show that certain elements of G₂ (acting in std₇) do not lie in this image.

Lemma 25.3. Given an element g ∈ GL(7), denote by (u_g, v_g) ∈ A² the point

(u_g, v_g) := (Trace(g), Trace(g²)).

Denote by R[U, V ] ∈ Z[U, V ] the two-variable polynomial

R[U, V ] := 8U³ –4U⁴ –4U⁵ + U⁶ + 4U²V –3U⁴V –4UV² + 3U²V² –V³.

We have the following results.

(1) For any ° ∈ SL(2, C), with image g := Sym⁶(°) ∈ SO(V₇), we have

R[u_g, v_g] = 0.

(2) There exist elements g in G₂(C) ⊂ SO(7) for which

R[u_g, v_g] ≠ 0.

(3) In the space UG^#₂ of conjugacy classes of UG₂, the set of points {g ∈ UG^#₂|R[u_g, v_g] = 0} is a closed set of (Haar) measure zero.

Proof. (1) Given ° ∈ SL(2, C), denote by x and 1/x its eigenvalues, and by t := x² + 1/x² the trace of its square. The eigenvalues of g := Sym⁶(°) are x⁶, x⁴, x², 1, 1/x², 1/x⁴, 1/x⁶. In terms of t = x² + 1/x², we have

Trace(g) = 1+ t + (t² – 2) + (t³ – 3t) = –1 – 2t + t² + t³ := f(t).

The trace of (°²)² is t² – 2, so we have

Trace(g²) = f(t² – 2) = –1+ 6t² – 5t⁴ + t⁶.

The resultant of the two polynomials in t given by

f(t) – U, f(t² – 2) – V,

is, according to Mathematica, R[U, V ]. Or one verifies by direct substitution that R[f(t), f(t² – 2)] = 0.

(2) Denote by ζ₃ ∈ C a primitive cube root of unity.There is an element g of G₂ with eigenvalues 1, ζ₃, ζ₃, ζ₃, ζ₃, ζ₃, ζ₃. For this element, we have Trace(g) = Trace(g²) = –2, and one checks that R[–2, –2] = 216.

(3) It suffices to show that in the maximal torus UT of UG₂, the locus R[u_g, v_g] = 0 has measure zero for Haar measure on UT, since the Herman Weyl measure on UT (i.e., the Weyl group-invariant measure on UT which induces (the direct image of) Haar measure on UG^#₂ ≅ UT/W) is absolutely continuous with respect to Haar measure. The function R[u_g, v_g] on UT ≅ S¹ × S¹ is a trigonometric polynomial, so it is either identically zero or its zero locus has measure zero. By part (2), it is not identically zero.

Lemma 25.4. Let k be a finite field of characteristic denoted p, a ∈ k^× an element. Suppose there exists a character χ of k^×, χ ≠ χ₂ if p ≠ 2, such that the element θ_a,k := (Frob_a,k|F(χ, k))^ss ∈ UG^#₂ has R[u_θa,k, v_θa,k] = 0. Then N(a, k) has G_geom = G_arith = G₂.

Proof. In view of the identity

det(1 – TFrob_k,χ|!(N(a, k))) = det(1 – TFrob_a,k|F(χ, k)),

we see that θ_a,k is equal to (Frob_k,χ|!(N(a, k))^ss. In view of Lemma 25.3, this element in UG^#₂ is not of the form Sym⁶(°) for any element ° ∈ SU(2)^#. This rules out the possibility that G_geom = G_arith is the image of SL(2) in Sym⁶(std_d), and the result now follows from Lemma 25.2.

Lemma 25.5. Let k be a finite field, F a lisse sheaf of rank seven on G_m/k which is pure of weight zero, orthogonally self-dual, and with G_geom = G_arith = G₂. Denote by α ∈ R_≥0 (resp. β ∈ R_≥0) the largest slope of F at 0 (resp. ∞). Then for any irreducible nontrivial representation Λ of G₂, we have the estimate

Proof. Consider the lisse sheaf Λ(F) of rank dim(Λ) obtained by “pushing out” F by Λ. By the Lefschetz Trace formula [Gr-Rat] and the vanishing of H²_c(G_m/k, Λ(F)), we have

By the Euler-Poincaré formula, we have

dim H¹_c(G_m/k, Λ(F)) = Swan₀(Λ(F)) + Swan_∞(Λ(F)).

By assumption, the upper numbering groups I(0)^α+ and I(∞)^β+ act trivially on F, so also on Λ(F), and so α (resp. β) are upper bounds for the slopes of F at 0 (resp. ∞). Thus we have

Swan₀(Λ(F)) ≤ α dim(Λ), Swan_∞(Λ(F)) ≤ β dim(Λ).

By Deligne’s main theorem [De-Weil II, 3.3.1], applied to the pure of weight zero lisse sheaf Λ(F), its H¹_c is mixed of weight ≤ 1, and the result follows.

Lemma 25.6. Let k_i be a sequence of finite fields whose cardinalities q_i tend to ∞. Suppose for each i we have a lisse sheaf F_i of rank seven on G_m/k_i which is pure of weight zero, orthogonally self-dual, and with G_geom = G_arith = G₂. Suppose there exist real numbers α ≥ 0 (resp. β ≥ 0) which are upper bounds for the slopes of every F_i at 0 (resp. at ∞). Let Z ⊂ UG^#₂ be a closed set of measure zero (for the induced Haar measure μ) in the space UG^#₂ of conjugacy classes of UG₂. For a_i ∈ k^×_i, denote by θ_ai,ki ∈ UG^#₂ the Frobenius conjugacy class (Frob_ai,ki|F_i)^ss. Then the fractions

tend to 0 as #k_i → ∞.

Proof. Denote by χ_Z the characteristic function of Z. Foreach i, denote by μ_i the probability measure on UG^#₂ given by

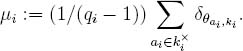
Then our ratios are the integrals ∫ χ_Zdμ_i. Pick a real number ² > 0. We will show that for #k_i sufficiently large, we have | ∫ χ_Zdμ_i| ≤ ².

Because Z has μ measure zero, we can find an open set V with Z ⊂ V ⊂ UG^#₂ and μ(V) ≤ ²/4. By Urysohn’s Lemma [Ru, 2.12], we can find a continuous R-valued function f on UG^#₂ with 0 ≤ f ≤ 1, with support in V and which is 1 on Z. Notice that

For each i we have

So it suffices to show

for #k_i sufficiently large.

By Peter-Weyl, we can find a finite linear combination of traces of irreducible representations Λ₀ = , Λ₁, …, Λ_n which is uniformly within ²/4 of f, say

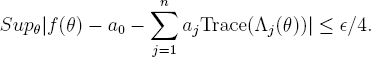
Then for every i we have

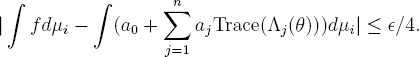
This same estimate holds for μ as well. We have seen that 0 ≤ ∫ fdμ ≤ ²/4, and hence we have

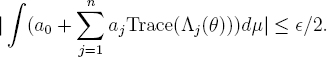
But in this integral, only the constant term survives, so we get

|a₀| ≤ ²/2.

Now let A := Sup_j|a_j|. It follows from the previous lemma, applied separately to each of the finitely many Λ_j, that for q_i := #k_i sufficiently large,¹ we will have

Then we get

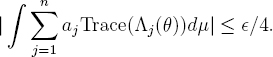
Thus from the above inequality

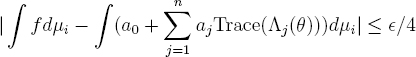
we see that

for #k_i sufficiently large.

Lemma 25.7. Let k_i be a sequence of finite fields whose cardinalities q_i tend to ∞. For each i take F_i := F(, k_i) in the previous lemma. Take for Z the closed set {g ∈ UG^#₂|R[u_g, v_g] = 0}. Then the fractions

tend to 0 as #k_i → ∞. Equivalently, the fractions

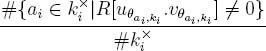
tend to 1 as #k_i → ∞.

Proof. Indeed the sheaves F_i are all tame at 0, and their ∞-slopes are either all 1/7, in characteristic 2, or they are 0 and six repetitions of 1/6. So we may take α = 0 and β = 1/6 in the previous lemma.

Combining this last lemma with Lemma 25.4, we see that Theorem 25.1 holds.

Remark 25.8. It seems plausible that every N(a, k) has G_geom = G_arith = G₂. Computer calculations show that this is the case if k = F_p with p ≤ 100, for every a ∈ F^×_p. Indeed, for these pairs (a, k), the element θ_a,k := (Frob_a,k|F(, k))^ss ∈ UG^#₂ has R[u_θa,k, v_θa,k] ≠ 0. [The skeptical reader will correctly object that we are merely avoiding a set of measure zero, namely R[u_g, v_g] = 0, hence these calculations are no evidence at all that every N(a, k) has G_geom = G_arith = G₂.]

¹The exact condition is that q_i be large enough that we have the inequalities (α + β)dim(Λ_j)√q_i/(q_i – 1) ≤ ∈/(4An) for j = 1, …, n.