CHAPTER 14

The Case of SL(2); the Examples of Evans and Rudnick

In treating both of these examples, as well as all the examples to come, we will use the Euler-Poincaré formula, cf. [Ray, Thm. 1] or [Ka-GKM, 2.3.1] or [Ka-SE, 4.6, (v) atop p. 113] or [De-ST, 3.2.1], to compute the “dimension” of the object N in question.

Let us briefly recall the general statement of the Euler-Poincaré formula, and then specialize to the case at hand. Let X be a projective, smooth, nonsingular curve over an algebraically closed field k in which ℓ is invertible, U ⊂ X a dense open set in X, and V ⊂ U a dense open set in U. Let G be a constructible Q_ℓ-sheaf on U which is lisse on V of rank r := gen.rk.(G). We view G|V as a representation of π₁(V). For each point x ∈ (X V)(k), we restrict this representation to the inertia group I(x) at x. Its Swan conductor gives a nonnegative integer Swan_x(G), cf. [Ka-GKM, 1.5-1.10], which vanishes if and only if G|V is tamely ramified at x. For each point u ∈ (U V)(k), we have the integer drop_u(G) := gen.rk.(G) – dim(G_u). We denote by χ(U) the Euler characteristic of U. Thus if X has genus g, then χ(U) = 2 – 2g – #(X U)(k). The Euler-Poincaré formula states that χ_c(U, G) = χ(U, G) is equal to

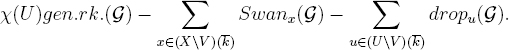
When U is G_m, whose χ vanishes, and we place G in degree –1, this becomes

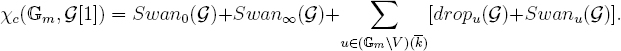
The term inside the square brackets, drop_u(G)+Swan_u(G), is called the “total drop” of G at u. Using this terminology, the formula becomes

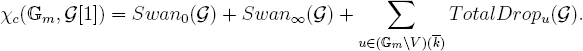
We now turn to the key result of this chapter.

Theorem 14.1. Suppose N in P_arith is pure of weight zero, geometrically irreducible, and arithmetically self-dual of “dimension” two. Then the following conditions are equivalent.

(1) N is geometrically Lie-irreducible.

(2) N is not geometrically isomorphic to any nontrivial multiplicative translate [x ax]^? N, a ≠ 1, of itself.

(3) N is symplectically self-dual, and we have G_geom,N = G_arith,N = SL(2).

Proof. The equivalence of (1) and (2) was proven in Corollary 8.3. If (3) holds, then G⁰_geom = SL(2) acts irreducibly in its standard representation, hence (1) holds. Conversely, suppose (1) holds. We will show that (3) holds. The autoduality on N is either orthogonal or symplectic. We first show it cannot be orthogonal. Indeed, if it were orthogonal, we would have G_geom,N ⊂ G_arith,N ⊂ O(2), with G_geom,N a Lie-irreducible subgroup of O(2). But there are no such subgroups, because SO(2) has index two in O(2) and is abelian. Therefore the autoduality must be symplectic. So we have inclusions G_geom,N ⊂ G_arith,N ⊂ SL(2), and hence it suffices to show that G_geom,N = SL(2). But the only irreducible (in the standard representation) subgroups of SL(2)/Q_ℓ are SL(2) itself, the normalizer N(T) of a torus T, and some finite subgroups. Of these, SL(2) is the only one that acts Lie-irreducibly.

With this result in hand, it is a simple matter to treat the examples of Evans and of Rudnick. We begin by treating the example of Evans.

Theorem 14.2. For à a nontrivial additive character of k, and N the object L_Ã(x–1/x)(1/2)[1] in P_arith on G_m/k := Spec(k[x, 1/x]), we have G_geom,N = G_arith,N = SL(2).

Proof. The lisse sheaf L_Ã(x–1/x) is pure of weight zero. It is wildly ramified at both 0 and ∞, with Swan conductor 1 at each, so is not geometrically isomorphic to an L_χ. Thus N is a geometrically irreducible object of P_arith, pure of weight zero. Its dimension “dim”N := χ(G_m / k, N) is given by the Euler-Poincaré formula,

χ(G_m / k, N) = Swan₀(L_Ã(x–1/x))+ Swan_∞(L_Ã(x–1/x)) = 1+ 1 = 2.

Writing L_Ã(x–1/x) = L_Ã(x) ⊗L_Ã(–1/x), we see by Theorem 10.1 that N is symplectically self-dual. The multiplicative translate of N by a ∈ k^× is L_{Ã(ax–1/ax)}(1/2)[1]. This is geometrically isomorphic to N if and only if L_{Ã(ax–1/ax)} is geometrically isomorphic to L_Ã(x–1/x), i.e., if and only if their ratio L_{Ã(ax–1/ax)} ⊗ (L_Ã(x–1/x))^–1 = L_{Ã((a–1)x+ (1–1/a)/x)} is geometrically trivial. But for a ≠ 1, this ratio is itself wildly ramified at both 0 and ∞. Therefore N is geometrically Lie-irreducible, and we conclude by the previous result.

Here is a strengthening of this result, using Theorem 12.1.

Theorem 14.3. Let c₁, …, c_r be r ≥ 2 elements of k^× whose squares are distinct: for i ≠ j, c_i ≠ ±c_j. Denote by N_i the object L_{Ã(ci(x–1/x))}(1/2)[1] on G_m/k := Spec(k[x, 1/x]). Then we have G_geom,⊕iNi = G_arith,⊕iNi = ∏^r_i=1 SL(2).

Proof. We must show that for i ≠ j, L_{Ã(ci(x–1/x))} is not geometrically isomorphic to either L_{Ã(cj(x–1/x))} or to [x –x]^? L_{Ã(cj(x–1/x))} = L_{Ã(–cj(x–1/x))}. As in the proof above, the ratio is L_{Ã((–ci±cj)(x–1/x))}. This is wildly ramified at both 0 and ∞, because for i ≠ j, –c_i ± c_j ≠ 0.

Here is a further strengthening of this result, again using Theorem 12.1. Its very formulation is based on the fact that for a given object N ∈ P_arith and a given Kummer sheaf L_χ, the functor M M ⊗ L_χ induces a Tannakian isomorphism of <N>_arith with <N ⊗ L_χ>_arith, and of <N>_geom with <N ⊗ L_χ>_geom. In particular N and N ⊗ L_χ have the “same” groups G_geom and the “same” groups G_arith as each other.

Theorem 14.4. Let c₁, …, c_r be r ≥ 1 elements of k^× whose squares are distinct: for i ≠ j, c_i ≠ ±c_j. Let χ₁, …, χ_s be s ≥ 1 distinct characters of k^×. Denote by N_i,j the object L_{Ã(ci(x–1/x))}⊗L_χj (1/2)[1] on G_m/k := Spec(k[x, 1/x]). Then we have G_{geom,⊕i,jNi,j} = G_{arith,⊕i,jNi,j} = ∏^r_i=1 ∏^s_j=1 SL(2).

Proof. We must show that for (i, j) ≠ (a, b), L_{Ã(ci(x–1/x))} ⊗ L_χj is not geometrically isomorphic to either L_{Ã(ca(x–1/x))} ⊗L_xb or to [x –x]^? L_{Ã(ca(x–1/x))} ⊗L_xb L_{Ã(–ca(x–1/x))} ⊗L_xb. [Recall that, geometrically, Kummer sheaves L_χ are invariant under multiplicative translation.] If i ≠ a, both ratios are wildly ramified at both 0 and ∞, just as in the proof of the previous result. If i = a but j ≠ b, then the ratio is either wildly ramified at both 0 and ∞, or it is Lχ_j/χ_b, which is not geometrically constant.

We now turn to the example of Rudnick in the split case.

Theorem 14.5. Suppose that k has odd characteristic. We work on G_m/k := Spec(k[x, 1/x]). For à a nontrivial additive character of k, form the lisse sheaf L_{Ã((x+ 1)/(x–1))} on U := G_m {1}. For j : U ⊂ G_m the inclusion, we have j_!L_{Ã((x+ 1)/(x–1))} = j_? L_{Ã((x+ 1)/(x–1))}. Form the object N := j_? L_{Ã((x+ 1)/(x–1))}(1/2)[1] on G_m/k. Then N is a geometrically irreducible two-dimensional object of P_arith which is pure of weight zero and arithmetically self-dual. It has G_geom,N = G_arith,N = SL(2).

Proof. The sheaf L_{Ã((x+ 1)/(x–1))} is wildly ramified at 1, so it is not geometrically isomorphic to an L_χ. Thus N is a geometrically irreducible object of P_arith, which is pure of weight zero. It is lisse at both 0 and ∞. Its only singularity in G_m is at 1, where its Swan conductor is 1. So the Euler-Poincaré formula, cf. [Ray] or [Ka-GKM, 2.3.1], shows that its dimension is two. It is symplectically self-dual, by Theorem 10.1 applied to the lisse sheaf F := L_{Ã((1/2)(x+ 1)/(x–1))} on U. And N is not geometrically isomorphic to a multiplicative translate of itself by any a ≠ 1, because 1 is the unique point of G_m(k) at which N is not lisse.

Here is a strengthening of this result, using Theorem 12.1.

Theorem 14.6. Let c₁, …, c_r be r ≥ 2 distinct elements of k^×. Form the object N_i := j_? L_{Ã(ci(x+ 1)/(x–1))}(1/2)[1] on G_m/k. Then we have G_geom,⊕iNi = G_arith,⊕iNi = ∏^r_i=1 SL(2).

Proof. We must show that for i ≠ j, L_{Ã(ci(x+ 1)/(x–1))} is not geometrically isomorphic to either L_{Ã(cj(x+ 1)/(x–1))} or to [x –x]^? L_{Ã(cj(x+ 1)/(x–1))}. The second isomorphism is impossible because the source is singular only at 1 ∈ G_m while the target is singular only at –1 ∈ G_m. For i ≠ j, L_{Ã(ci(x+ 1)/(x–1))} is not geometrically isomorphic to L_{Ã(cj(x+ 1)/(x–1))} because their ratio, L_{Ã((cj–ci)(x+ 1)/(x–1))}, is wildly ramified at 1.

Here is a further strengthening, again using Theorem 12.1.

Theorem 14.7. Let c₁, …, c_r be r ≥ 1 distinct elements of k^×. Let χ₁, …, χ_s be s ≥ 1 distinct characters of k^×. Denote by N_a,b the object N_a,b := j_? L_{Ã(ca(x+ 1)/(x–1))} ⊗L_xb(1/2)[1] on G_m/k. Then we have G_{eom,⊕a,bNa,b} = G_{arith,⊕a,bNa,b} = ∏^r_a=1 ∏^s_b=1 SL(2).

Proof. All the objects N_a,b have the point 1 as their unique singularity, so just as in the argument above it suffices to show that for (a, b) ≠ (c, d), N_a,b is not geometrically isomorphic to N_c,d. If a ≠ b, then just as above the ratio is wildly ramified at 1. If a = b but c ≠ d, the ratio is Lχ_d/χ_c, which is not geometrically constant.

We conclude this chapter with the example of Rudnick in the non-split case. Here k has odd characteristic. Completing the square, we can present k₂ as k[u]/(u² + b) with b ∈ k^× and u² + b ∈ k[u] quadratic (and irreducible, but we will not use this). For any k-algebra A, we write elements of A ⊗_k k₂ as x + yu, with x, y ∈ A.

Then G/k = Spec(k[x, y]/(x² + by² – 1)). The group law is
(x, y)(s, t) := (xs – byt, xt + ys),

the identity is (1, 0), and inversion is

[inv]^? (x, y) = (x, –y).

On the open set G[1/(x – 1)] where x – 1 is invertible, we have the function –by/(x – 1), which changes sign under inversion:

[inv]^? (–by/(x – 1)) = by/(x – 1).

In the split case, i.e., when –b = c² for some c ∈ k^×, then (x, y) t := x + cy is an isomorphism G ≅ G_m. Then we readily calculate¹

–by/(x – 1) = c(t + 1)/(t – 1).

Theorem 14.8. Suppose that k has odd characteristic. For à a nontrivial additive character of k, form the lisse sheaf L_{Ã(–by/(x–1))} on U := G[1/(x – 1)]. For j : U ⊂ G the inclusion, we have j_!L_{Ã(–by/(x–1))} = j_? L_{Ã(–by/(x–1))}. Form the object N := j_? L_{Ã(–by/(x–1))}(1/2)[1] on G/k. Then N is a geometrically irreducible two-dimensional object of P_arith which is pure of weight zero and arithmetically self-dual. It has G_geom,N = G_arith,N = SL(2).

Proof. That j_? L_{Ã(–by/(x–1))} is not geometrically a Kummer sheaf L_χ is a geometric statement, already proven in the split case, as is the fact that N is geometrically irreducible two-dimensional object of P_arith. That it is pure of weight zero is obvious from its definition. That it is arithmetically symplectically self-dual results from Theorem 10.1, applied to L_{Ã(–by/2(x–1))}. The rest of the proof is the same as in the split case.

For the sake of completeness, here are the strengthenings in the nonsplit case, with the same proofs as in the split case.

Theorem 14.9. Let c₁, …, c_r be r ≥ 2 distinct elements of k^×. Form the object N_i := j_? L_{Ã(–bciy/(x–1))}(1/2)[1] on G/k. Then we have G_geom,⊕iNi = G_arith,⊕iNi = ∏^r_i=1 SL(2).

Theorem 14.10. Let c₁, …, c_r be r ≥ 1 distinct elements of k^×. Let χ₁, …, χ_s be s ≥ 1 distinct characters of G(k). Denote by N_i,j the object N_i,j := j_? L_{Ã(–bciy/(x–1))} ⊗ L_χj (1/2)[1] on G/k. Then we have G_{geom,⊕i,jNi,j} = G_{arith,⊕i,jNi,j} = ∏^r_i=1 ∏^s_j=1 SL(2).

¹Indeed, t = x + cy, 1/t = x – cy, so 2cy = t – 1/t = (t + 1)(t – 1)/t, 2x – 2 = t + 1/t – 2 = (t – 1)²/t, hence cy/(x – 1) = (t + 1)/(t – 1).