CHAPTER 20

GL(n) × GL(n) × … × GL(n) Examples

In this chapter, we investigate the following question. Suppose we have a geometrically irreducible middle extension sheaf G on G_m/k which is pure of weight zero, such that the object N := G(1/2)[1] ∈ P_arith has “dimension” n and has G_geom,N = G_arith,N = GL(n). Suppose in addition we are given s ≥ 2 distinct characters χ_i of k^×. We want criteria which insure that for the objects

N_i := N ⊗ L_χi,

the direct sum ⊕_iN_i has G_geom,⊕iNi = G_arith,⊕iNi = ∏_i GL(n). Because we have a priori inclusions G_geom,⊕iNi ⊂ G_arith,⊕iNi ⊂ ∏_i GL(n), it suffices to prove that G_geom,⊕iNi = ∏_i GL(n). To show this, it suffices to show both of the following two statements.

(1) The determinants in the Tannakian sense “det”(N ⊗ L_χi) := “det”(N_i) have G_{geom,⊕i“det”(Ni)} = ∏_iGL(1).

(2) (G_geom,⊕iNi)^0,der = ∏_i SL(n).

We first deal with the Tannakian determinants. As already noted, M → M ⊗ L_χ is a Tannakian isomorphism from <N>_geom to <N ⊗ L_χ>_geom. In particular, the Tannakian determinants satisfy

“det”(N ⊗ L_χ) = “det”(N) ⊗L_χ.

Now “det”(N) is a nonpunctual (because it is of infinite order) one-dimensional object of <N>_geom, so it is a multiplicative translate of an irreducible hypergeometric H(Ã; ρ_a′s;Λ_b′s)[1] of some type (n, m), n, m ≥ 0, n + m > 0, cf. [Ka-ESDE, 8.5.3]. The irreducibility is equivalent to the condition that, if both n and m are ≥ 1, no ρ_a is any Λ_b, cf. [Ka-ESDE, 8.4.2, 8.4.10.1]. We have the following lemma, which we will apply with its M taken to be “det”(N).

Lemma 20.1. Suppose M ∈ P_geom is a multipliplicative translate of an irreducible hypergeometric H(Ã; ρ_a′s;Λ_b′s)[1] of some type (n, m), n, m ≥ 0, n + m > 0. [Thus if both n and m are ≥ 1, no ρ_a is any Λ_b.] Suppose given s ≥ 2 distinct characters χ_i of k^×, which satisfy the following three conditions.

(1) If both n and m are ≥ 1, then for i ≠ j, no χ_iρ_a is any χ_jΛ_b.

(2) If n > 0, then for i ≠ j, no χ_iρ_a is any χ_jρ_a′.

(3) If m > 0, then for i ≠ j, no χ_iΛ_b is any χ_jΛ_b′.

Then with M_i := M ⊗ L_χi, we have G_geom,⊕iMi = ∏_i GL(1).

Proof. We must show that for any nonzero vector υ = (υ₁, …, υ_s) ∈ Z^s, the tensor product in the Tannakian sense M^⊗υ₁ ⊗ M₂^⊗υ₂ … ⊗ M_s^⊗υ_s is not geometrically trivial. Omitting terms which don’t occur, and renumbering, we must show the following two statements.

(1) If v₁, υ₂, …, υ_r are ≥ 1, then the tensor product in the Tannakian sense M₁^⊗υ1 … ⊗ M_r^⊗υr is not geometrically trivial.

(2) If υ₁, υ₂, …, υ_r are ≥ 1 and υ_{r+ 1}, …, υ_{r+ t} are ≤ –1, say υ_i = –w_i for r + 1 ≤ i ≤ r + t, then then the tensor product in the Tannakian sense ⊗ M₂^⊗_υ2 … ⊗ M_r^⊗υ_r is not geometrically isomorphic to the tensor product in the Tannakian sense .

To see the truth of these statements, recall from [Ka-ESDE, 8.3.3 and 8.4.13.1] that given two irreducible hypergeometrics H(Ã; ρ_a′s;Λ_b′s)[1] and H(Ã; μ_c′s; ν_d′s)[1] of types (n, m) and (e, f) respectively, so long as no ρ_a is a ν_d and no Λ_b is a μ_c, then their ! convolution maps isomorphically to their ? convolution. This common convolution is their middle convolution, which is the irreducible hypergeometric of type (n + e, m + f) given up to geometric isomorphism by

H(Ã; ρ_a′s;Λ_b′s)[1] ?_mid H(Ã; μ_c ′s; ν_d ′s)[1]

≅ H(Ã; ρ_a′s ∪ μ_c′s;Λ_b′s ∪ ν_d′s)[1].

Recall also [Ka-ESDE, 8.2.5] that for any χ we have

H(Ã; ρ_a′s;Λ_b′s)[1] ⊗L_χ ≅ H(Ã; χρ_a′s; χΛ_b′ s)[1].

In case (1), hypothesis (1), if relevant, allows us to compute the tensor product in the Tannakian sense M₁^⊗υ₁ … ⊗ M_r^⊗υ_r. It is a multiplicative translate of the irreducible hypergeometric of type (n∑_i υ_i, m ∑_i υ_i) whose “upstairs” parameters (the tame part of local monodromy at 0) if any are the χ_iρ_a with various repetitions, and whose “downstairs” parameters (the tame part of local monodromy at ∞) if any are the χ_jΛ_b with various repetitions, with i, j in [1, r].

In case (2), M₁^⊗υ₁ … ⊗ M₁^⊗υ_r is a multiplicative translate of the hypergeometric of type (n ∑_i υ_i, m ∑_i υ_i) whose “upstairs” parameters are the χ_iρ_a with various repetitions, and whose “downstairs” parameters are the χ_jΛ_b with various repetitions, with i, j in [1, r]. And is a multiplicative translate of the hypergeometric of type (n ∑_j w_r+j, m ∑_j w_r+j) whose “upstairs” parameters are the χ_r+jρ_a with various repetitions, and whose “downstairs” parameters are the χ_r+jΛ_b with various repetitions, with i, j in [1, t]. If n > 0 (resp. if m > 0), then the tame parts of local monodromy at 0 (resp. at ∞) of both sides are nonzero, but by the disjointness hypotheses (2) (resp. (3)), they have completely disjoint characters at 0 (resp. at ∞). So they are not geometrically isomorphic.

Here is a simple but striking case, which gives a more compact packaging of the proof in [Ka-GKM, 9.3, 9.5] of a result on equidistribution in (S¹)^r of r-tuples of angles of Gauss sums.

Corollary 20.2. Fix a nontrivial additive character à of k, L_à the corresponding Artin-Schreier sheaf, and put N := L_Ã(1/2)[1] ∈ P_arith. For any r ≥ 1 distinct characters χ_i of k^×, put N_i := N ⊗ L_χi. The object ⊕_iN_i has

Proof. L_Ã is H(Ã; , ), a hypergeometric of type (1, 0), with the only ρ of the previous lemma the trivial character .

Another simple case is this, which, with a = 1, gives an equidistribution result in (S¹)^r for r-tuples of angles of Jacobi sums.

Corollary 20.3. Fix a nontrivial multiplicative character Λ of k^×, and an element a ∈ k^×. Put N := L_Λ(a–x)(1/2)[1] ∈ P_arith. Choose r ≥ 1 distinct characters χ_i of k^×, put N_i := N ⊗ L_χi. Suppose that for all i ≠ j, χ_i ≠ Λχ_j. Then the object ⊕_iN_i has

Proof. Indeed, L_Λ(a–x) is a multiplicative translate of the hypergeometric H(, Λ) of type (1, 1). Here the only ρ of Lemma 20.1 is , and the fixed Λ is the only Λ.

We now turn to the problem of showing that for a given N with G_geom,N = G_arith,N = GL(n), we have (G_geom,⊕_iN⊗L_χi)⁰, der = ∏_i SL(n). Put N_i := N ⊗ L_χi. By Theorem 13.5 (Goursat-Kolchin-Ribet), it suffices to show that for every one-dimensional object L ∈ P_geom, and for i ≠ j, there is no geometric isomorphism between N_i and N_j ?_mid L nor between N_i and N^∨_j ?_mid L.

To deal with an L which is punctual, we must show that for i ≠ j, there is no geometric isomorphism between N_i and any multiplicative translate of either N_j or of N_j^∨.

To deal with an L which is nonpunctual, we consider the generic rank gen.rk(M) of objects M ∈ P_geom. Onadenseopenset U ⊂ G_m/k, M|U is F[1] for a lisse sheaf F on U. The rank of F on U is by definition gen.rk(M). Clearly two objects of different generic rank cannot be geometrically isomorphic.

Theorem 20.4. Suppose N = G[1] ∈ P_geom, with G an irreducible middle extension sheaf on G_m/k. Suppose that either of the following two conditions is satisfied.

(1) “dim”(N) ≥ 3, G is tame at 0 and ∞, and its local monodromies at 0 and ∞ both satisfy the following condition: if a character χ occurs, it occurs in a single Jordan block.

(2) G is the restriction to G_m of a sheaf which is lisse on A¹/k, totally wild at ∞, with all of its ∞-slopes > 2.

Then for any nonpunctual one-dimensional object L ∈ P_geom, we have

gen.rk(N ?_mid L) > gen.rk(N)

and

gen.rk(N^∨ ?_mid L) > gen.rk(N).

Proof. An object and its dual have the same generic rank. The dual of N^∨ ?_mid L is N ?_mid L^∨, and L^∨ is again a nonpunctual one-dimensional object. So it suffices to prove the first inequality, gen.rk(N ?_mid L) > gen.rk(N).

We next explain how to calculate the generic rank of our middle convolution N ?_mid L. The nonpunctual one-dimensional object L is H[1], for H a multiplicative translate of an irreducible hypergeometric sheaf, cf. [Ka-ESDE, 8.5.3]. Over a dense open set U ⊂ G_m/k, both N ?_! L and N ?_? L are lisse sheaves placed in degree –1, and of formation compatible with arbitrary change of base on U. So the middle convolution

N ?_mid L := Image(N_?! L → N ?_? L)

is, on U, itself a lisse sheaf placed in degree –1, and of formation compatible with arbitrary change of base on U.

Denote by S and T respectively the singularities of G and H in G_m. Fix a point a ∈ U(k) which, if both S and T are nonempty, does not lie in the set ST of products. Form the sheaf K on G_m defined by

K := G ⊗ [x a/x]^?H.

Notice that K is itself a middle extension sheaf on G_m (because a does not lie in ST), and denote by j : G_m ⊂ P¹ the inclusion. Then the stalks at a of N_?! L, N ?_? L, and N ?_mid L respectively are the cohomology groups

H¹(P¹/k, j_!K), H¹(P¹/k, Rj_? K), H¹(P¹/k, j_? K)

respectively. We have a short exact sequence of sheaves on P¹,

0 → j_!K → j_? K → (K(0)^I(0))_{pct. at} 0 ⊕ (K(∞)^I(∞))_{pct. at ∞} → 0.

We first observe that in the long exact cohomology sequence, for i ≠ 1, both Hⁱ(P¹/k, j_!K)(= Hⁱ_c(G_m/k, K)) and Hⁱ(P¹/k, j_? K) vanish. The H⁰_c vanishes because K has no nonzero punctual sections. The H²_c and the H⁰ vanish because N = G[1] and hence N^∨ both have “dim”(N) > 2, so N^∨ is geometrically isomorphic to no multiplicative translate of [x 1/x] ^?L, which has “dimension” one. The H²(P¹/k, j_? K) vanishes because it is a quotient of H²_c(P¹/k, j_!?K).

So the long exact cohomology sequence gives a short exact sequence

0 → K(0)^I(0) ⊕K(∞)^I(∞) → H¹(P¹/k,_{j ?} K) → H¹(P¹/k,_{j ?} K) → 0.

Thus we obtain the formula

gen.rk(N?_mid L) = gen:rk(N _?! L) = dim K(0)^I(0) – dim K(∞)^I(∞).

We will now calculate each of the three terms on the right-hand side. The sheaf K is lisse outside the disjoint union S ∪a/T.

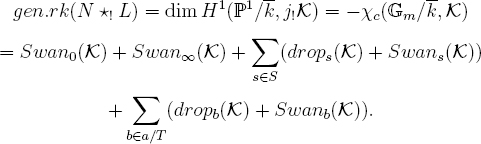
For s ∈ S, H is lisse at a/s, so we have

drops_s(K) + Swans_s(K) = (drops_s(G) + Swans_s(G))gen:rk(H).

For b = a/t ∈ a/T, G is lisse at b, so we have

drop_b(K) + Swan_b(K) = gen:rk(G)(drop_t(H) + Swan_t(H)).

We first treat case (1). Thus G is tame at both 0 and ∞. Here we have

Swan₀(K) = gen:rk(G)Swan_∞(H).

Swan_∞(K) = gen:rk(G)Swan₀(H).

In this case, the above plethora of formulas gives the relation

gen:rk(N ?_! L) = gen:rk(N) “dim”(L) + “dim”(N)gen:rk(L).

We next derive, in this case, upper bounds for dim K(0)^I(0) and for dim K(∞)^I(∞). To do this, write

H(0) = H(0)^tame ⊕ H(0)^tot.wild,

H(∞) = H(∞)^tame ⊕ H(∞)^tot.wild.

The isomorphism classes of both H(∞)^tame and H(0)^tame are invariant under multiplicative translation. Define

inυH := [x 1/x] ^? H.

Then we have

K(0)^I(0) ≅ (G(0) ⊗ inυH(0)^tame)^I(0),

K(∞)^I(∞) ≅ (G(∞) ⊗ inυH(∞)^tame)^I(∞).

Now we make use of the hy pothesis on G that its local monodromies at both 0 and ∞ satisfy the condition that any character that occurs does so in a single Jordan block. One knows [Ka-ESDE, 8.4.2 (6-8)] that the tame parts of the local monodromies of H and hence of inυH at both 0 and ∞ also satisfy this condition. We claim that

dim K(0)^I(0) ≤ Min(gen.rk(G), rk(inυH(0)^tame)),

dim K(∞)^I(∞) ≤ Min(gen.rk(G), rk(inυH(∞)^tame)).

Granting these claims, we can conclude as follows. It suffices to show that

gen:rk(N)“dim” (L)+ “dim” (N)gen:rk(L) – 2 Min(gen:rk(G), gen:rk(H)) > gen:rk(N).

Now “dim” (L) = 1, so this is equivalent to showing that

“dim” (N)gen:rk(L) > 2 Min(gen:rk(G); gen:rk(H)).

But gen:rk(L) := gen:rk(H), we may rewrite this as

“dim” (N)gen:rk(H) > 2 Min(gen:rk(G); gen:rk(H)).

But we have the trivial inequality gen:rk(H) ≥ Min(gen:rk(G); gen:rk(H)), so it suffices that

“dim” (N)gen:rk(H) > 2gen:rk(H),

which is obvious from the assumption that “dim” (N) ≥ 3.

It remains to show that

dim K(0)^I(0) ≤ Min(gen:rk(G); rk(inυH(0)^tame)),

dim K(∞)^I(∞) ≤ Min(gen:rk(G); rk(inυH(∞)^tame)).

Recall that

K(0)^I(0) ≅ (G(0) ⊗ inυH(0)^tame)^I(0),

K(∞)^I(∞) ≅ (G(∞) ⊗ inυH(∞)^tame)^I(∞).

So we must show that

dim(G(0) ⊗ inυH(0)^tame)^I(0) ≤ Min(gen.rk(G), rk(inυH(0)^tame)),

dim(G(∞) ⊗ inυH(∞)^tame)^I(∞) ≤ Min(gen.rk(G), rk(inυH(∞)^tame)).

It suffices to prove the (universal truth of the) first. Thus we have a tame representation V of I(0)

of rank n = ∑_i n_i, in which the χ_i are all distinct. And we have a second tame representation W of I(0),

of rank m = ∑_j m_j, in which all the ρ_j are distinct. We must show that

dim((V ⊗ W)^I(0)) ≤ Min(n, m).

Now

The only terms with nonzero I(0)-invariants are those for which χ_i = ρ_j. If there are no such pairs, there is nothing to prove. If there are such pairs, we may renumber so that χ_i = ρ_i for i = 1, …, r, and χ_i ≠ ρ_j unless i = j and 1 ≤ i, j ≤ r. So we may replace V by its subspace Lχ_i ⊗ Unip(n_i) and replace W by its subspace Lχ_i ⊗ Unip(m_i). So we are reduced to showing that

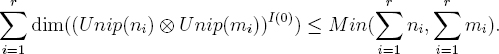
We have the trivial inequality

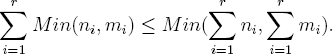
So it suffices to observe that for two integers n, m ≥ 1, we have

dim((Unip(n) ⊗ Unip(m))^I(0)) = Min(n, m).

To fix ideas, say m ≤ n. One knows that

Unip(n) ⊗ Unip(m) = Sym^n–1(Unip(2)) ⊗ Sym^m–1(Unip(2))

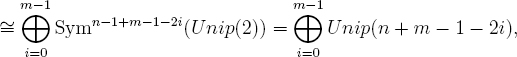
and each of the m unipotent Jordan block summands has a one-dimension space of I(0)-invariants. This concludes the proof in case (1).

We now treat case (2). Thus G is the restriction to G_m of a sheaf which is lisse on A¹/k, totally wild at ∞, with all of its ∞-slopes > 2. Recall that

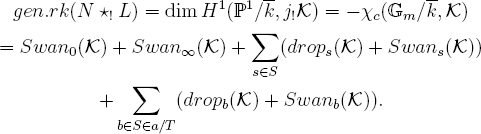
Here S is empty. For b = a/t ∈ a/T, G is lisse at b, so we have

drop_b(K)+ Swan_b(K) = gen.rk(G)(drop_t(H)+ Swan_t(H)).

Because G is lisse at 0, we have

Swan₀(K) = gen.rk(G)Swan_∞(H).

Because G has all its ∞-slopes > 2, while every ∞-slope of [x a/x]^?H is ≤ 1, we have

Swan_∞(K) = gen.rk(H)Swan_∞(G).

Putting all these together, we get the formula

gen.rk(N ?_!L) = gen.rk(G)(“dim”(L)–Swan₀(H))+ “dim”(N)gen.rk(L).

Meanwhile K is totally wild at ∞, so K(∞)^I(∞) = 0. As G is lisse at 0,

dim(K^I(0)) = gen.rk.(G) dim(invH(0)^I(0)).

Now “dim”(L) = 1, and both Swan₀(H) and dim(invH(0)^I(0)) are ≤ 1. So we have the inequality

gen.rk(N ?_! L) ≥ “dim”(N)gen.rk(L) – gen.rk.(G).

We will show that

“dim”(N)gen.rk(L) – gen.rk.(G) > gen.rk.(G),

i.e., that

“dim”(N)gen.rk(L) > 2gen.rk.(G).

As gen.rk(L) ≥ 1, it suffices to show that

“dim”(N) > 2gen.rk.(G).

But “dim”(N) = Swan_∞(G) is the sum of the gen.rk(G) ∞-slopes of G, each of which is > 2, so this last inequality is obvious.

With these results in hand, it is a simple matter to apply them to the GL(n) examples we have found in Chapter 17.

Theorem 20.5. Fix any integer n ≥ 3, and a lisse rank one sheaf F on A¹/F_p which is pure of weight zero and whose Swan conductor at ∞ is the integer n, such that F|G_m is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Thus the object N := F(1/2)[1] ∈ P_arith has “dim”(N) = n, and G_geom,N = G_arith,N = GL(n). For any r ≥ 2 distinct characters χ_i of k^×, put N_i := N ⊗ L_χi. Then the object ⊕_iN_i has

Proof. We first show that for i ≠ j, there is no geometric isomorphism between N_i and any multiplicative translate of either N_j or N^∨_j. Any multiplicative translate of N^∨_j is totally wild at 0, while N_i is tame at 0. And N_i and any multiplicative translate of N_j have nonisomorphic local monodromies at 0, namely L_χi and L_χj.

To show that for a nonpunctual L ∈ P_geom of “dimension” one there is no geometric isomorphism of N_i with either N_j ?_mid L or N^∨_j ?_mid L, we “pull out” the L_χj :

N_j ?_mid L = (N ⊗ L_χj) ?_mid L ≅ (N ?_mid (L ⊗ L_χj)) ⊗ L_χj.

Now N and each N_j have the same generic rank as each other, so by the previous result we get

gen.rk(N_j ?_mid L) > gen.rk(N_i).

Writing

N^∨_j ?_mid L = (N^∨ ⊗ L_χj) ?_mid L ≅ (N^∨ ?_mid (L ⊗ L_χj)) ⊗ L_χj,

and putting L₁ := L ⊗ L_χj, we observe that N^∨ ?_mid L₁ has the same generic rank as its Tannakian dual N ?_mid L^∨₁, so we get

gen.rk(N^∨_j ?_mid L) > gen.rk(N_i).

To show that the Tannakian determinants “det”(N_i) = (det N) ⊗ L_χi are independent, it suffices, by Corollary 20.2, to show that “det”(N) is geometrically isomorphic to a multiplicative translate of the Artin Schreier sheaf L_Ã(1/2)[1], Ã some fixed nontrivial additive character of k. For this we argue as follows. One knows that the collection of all objects in P_geom which are lisse on G_m, unipotent at 0, and totally wild at ∞ is stable by ! convolution, which coincides, on this collection, with middle convolution, cf. [Ka-GKM, 5.1 (2)]. So “det”(N), a direct factor of the n-fold convolution of N with itself, is lisse on G_m, totally wild at 0, and unipotent at 0. The only such objects of “dimension” one are (shifts by [1] of) multiplicative translates of Kloosterman sheaves Kl_n := Kl(Ã; , …, )(n/2) of some rank n ≥ 1, cf. [Ka-ESDE, 8.5.3]. Because “det”(N) ∈ P_arith, the multiplicative translation must be by an a ∈ k^×. It remains to see that n = 1. For this we consider the weight drop of Frob_k, acting on “det”(N). Acting on N, it has n – 1 eigenvalues of absolute value 1, and one eigenvalue of absolute value 1/√#k. So acting on “det”(N), its weight drop is one. In general, the weight drop of Frob_k, acting on !(Kl_n(n/2)[1]) ≅ H¹_c(G_m/k, Kl_n(n/2)) is n, cf. [Ka-GKM, 7.3.1].

Theorem 20.6. Let k have odd characteristic. Fix an odd integer n ≥ 3, and define N := Symⁿ(Leg)((n + 1)/2)[1] in P_arith, which we have seen (Theorem 17.2) is pure of weight zero, has “dimension” n, and has

G_geom,N = G_arith,N = GL(n).

Let χ₁, …, χ_r be characters of k^× whose squares are all distinct, i.e., for i ≠ j, χ_i/χ_j is neither trivial nor is it the quadratic character. Put N_i := N ⊗ L_χi. Then the object ⊕_iN_i has

Proof. The objects N_i and their Tannakian duals N^∨_i all have the point 1 as their unique singularity in G_m, and all are tame at 0 and ∞. So none is geometrically isomorphic to a nontrivial multiplicative translate of another. The local monodromy of N at 0 is Unip(n + 1), and that of N^∨ at 0 is L_χquad ⊗ Unip(n + 1), so for i ≠ j, N_i is not geometrically isomorphic to either N_j or N^∨_j. We may apply Theorem 20.4 to show that no N_i is isomorphic to any N_j ?_mid L or to any N^∨_j ?_mid L for any nonpunctual one-dimensional object L. The generic rank method applies, because all the N_i and N^∨_i have the same generic rank n + 1, and are tame at 0 and ∞, with local monodromy at each a single Jordan block of size n + 1.

It remains to show how to apply Lemma 20.1 to “det”(N). As explained in the proof of Theorem 17.2, the only bad characters for N are the trivial character and the quadratic character χ₂. For , n – 1 of the Frobenius eigenvalues have absolute value 1, and the remaining eigenvalue has absolute value (1/√#k)^{n+ 1}. For χ₂, n – 1 of the Frobenius eigenvalues have absolute value 1, and the remaining eigenvalue has absolute value (√#k)^{n+ 1}. So “det”(N) is geometrically isomorphic to a multiplicative translate of H[1] for H the hypergeometric of type (n + 1, n + 1) given by H(Ã; , …, ; χ₂, …, χ₂). And by Lemma 19.3, there is in fact no multiplicative translate.^?

We also have the following generalization.

Theorem 20.7. Let n ≥ 3 be an integer, and χ a character of k^× such that χ² has order > n. Form the hypergeometric sheaf H := H(!, Ã;1, χ²; χ, χ), and the object N := Symⁿ(H)((3n + 1)/2)[1] in P_arith, which (by Theorem 17.3) is pure of weight zero, has “dimension” n, and has

G_geom,N = G_arith,N = GL(n).

Let ρ₁, …, ρ_r be r ≥ 2 characters of k^×, such that for i ≠ j, ρ_i/ρ_j is not on either of the following two lists:

{χ^2n–2j}_{j=0, …, 2n}, {χ^n–2j}_{j=0, …, n.}

Put N_i := N ⊗ L_χi. Then the object ⊕_iN_i has

Proof. The objects N_i and their Tannakian duals N^∨_i all have the point 1 as their unique singularity in G_m, and all are tame at 0 and ∞. So none is geometrically isomorphic to a nontrivial multiplicative translate of another. The local monodromy of N at 0 is ⊕ⁿ_j=0L_χ^2j, and that of N^∨ at 0 is L_χⁿ ⊗ Unip(n + 1). In view of the hypotheses made on the ratios of the ρ_i, we see from the local monodromies at 0 that for i ≠ j, N_i is not geometrically isomorphic to either N_j or N^∨_j. We use Theorem 20.4 to show that no N_i is isomorphic to any N_j ?_mid L or to any N^∨_j ?_mid L for any nonpunctual one-dimensional object L.

To apply Lemma 20.1 to “det”(N), recall from the proof of Theorem 17.3 that this Tannakian determinant is geometrically isomorphic to H[1] for H the hypergeometric sheaf of type (n, n) given by H(Ã; χ², …, χ²ⁿ; , …, ).

To conclude this chapter, we consider our fourth example of a GL(n) object. Recall that in Theorem 17.5 we took a polynomial f[x] = ∑ⁿ_i=0 A_ixⁱ in k[x] of degree n ≥ 2 with all distinct roots in k. We supposed that f(0) = 0, and that gcd{i|A_i ≠ 0} = 1, and we took a character χ of k^× such that χⁿ is nontrivial. We then formed the object N := L_χ(f)(1/2)[1] in P_arith, which we showed was pure of weight zero, had “dimension” n, and had

G_geom,N = G_arith,N = GL(n).

In order to apply Theorem 20.4, we need to assume n ≥ 3 in the following theorem.

Theorem 20.8. Suppose n ≥ 3, and consider the object N := L_χ(f)(1/2)[1] of the previous paragraph. Let ρ₁, …, ρ_r be r ≥ 2 characters of k^×, such that for i ≠ j, χ_i/χ_j is neither the trivial character nor the character χⁿ. Put N_i := N ⊗ L_χi. Then the object ⊕_iN_i has

Proof. Recall from the proof of Theorem 17.5 that in this case the Tannakian determinant “det”(N) is geometrically isomorphic to H[1] for H = H(Ã; ; χⁿ) ≅ L_χn(1–x). So by Lemma 20.1 the determinants of the N_i are independent.

Because we assume n ≥ 3, we may apply Theorem 20.4 to show that no N_i is isomorphic to any N_j ?_mid L or to any N^∨_j ?_mid L for any nonpunctual one-dimensional object L. It remains to show that for i ≠ j, N_i is not geometrically isomorphic to any multiplicative translate of either N_j or of N^∨_j. To see this, we compare local monodromies at ∞. For N_i it is L_χⁿρi. For N_j it is L_χⁿρj, and for N^∨_j it is L_ρj, all of whose geometric isomorphism classes are invariant under multiplicative translation. By the hypothesis on the characters ρ_k, these local monodromies are in three distinct isomorphism classes.