CHAPTER 21

SL(n) Examples, for n an Odd Prime

In this chapter, we will construct, for every n ≥ 3, n-dimensional objects with G_geom ⊂ G_arith ⊂ SL(n), but only when n is prime will we be able to prove that G_geom = G_arith = SL(n).

Theorem 21.1. Let k be a finite field of characteristic p, Ã a nontrivial additive character of k. Let f (x) = ∑ ^a_i=–b A_ixⁱ ∈ k [x, 1/x] be a Laurent polynomial of “bidegree” (a, b), with a, b both ≥ 1 and both prime to p. Assume further that f (x) is Artin-Schreier reduced. Thus A_a A_–b ≠ 0, and A_i ≠ 0 implies that i is prime to p. We have the following results.

(1) The object N := L_Ã(f(x))(1/2)[1] ∈ P_arith is pure of weight zero, geometrically irreducible, and of “dimension” a + b.

(2) If (–1)^aa A_a = (–1)^b+1bA_–b, then G_geom,N ⊂ SL(a + b). In general, the Tannakian determinant “det” (N) is geometrically isomorphic to δ_α, for α = (–1)^b+1bA_–b/(–1)^aaA_a. And setting

β := det(Frob_k,|!(N)),

we have the arithmetic determinant formula

“det”(N) = β^deg ⊗ δ_α.

(3) If a = b, then N is not Lie-self-dual, i.e., G⁰_{geom, N} lies in no orthogonal group SO(a + b), and, if a + b is even, it lies in no symplectic group Sp(a + b).

(4) Suppose in addition that gcd{i|A_i ≠ 0} = 1. Then N is geometrically Lie-irreducible, i.e., G⁰_{geom, N} is an irreducible subgroup of SL(a + b) (in the given a + b-dimensional representation).

Proof. The sheaf L_Ã(f(x)) is lisse of rank one (and a fortiori geometrically irreducible) and pure of weight zero on G_m, with Euler characteristic –S_wan0 – S_wan∞ = –a – b, so (1) is obvious. Let us admit the truth of (2) for the moment. To show that N is not Lie-self-dual when a ≠ b, it suffices to show that for any integer d ≥ 1 prime to p, the d’th power direct image [d]^_?N is not geometrically isomorphic to its Tannakian dual. But this object has different Swan conductors at 0 and ∞, namely a and b respectively, while its Tannakian dual [x 1/x] ^?D([d]_?N) has Swan conductors b and a respectively at 0 and ∞. If in addition gcd{i|A_i ≠ 0} = 1, the geometric Lie-irreducibility of N follows from Corollary 8.3. Indeed, this gcd = 1 hypothesis and the fact that f is Artin-Schreier reduced together insure that for any a ≠ 1 in k^×, N is not geometrically isomorphic to [x ax] ^?N, cf. the proof of Theorem 14.2.

We now turn to the calculation of the Tannakian determinant “det”(N). We will compute, for every finite extension field E/k, and every character χ of E^×,

det(Frob_E,χ|!(N)) = det(Frob_E|H⁰(A¹ ⊗_k k, j_0!(N ⊗ L_χ))).

Because N is totally wild at both 0 and ∞, this is

= det(Frob_E|H⁰_c(G_m ⊗_k k, N ⊗ L_χ))

= det(Frob_E|H¹_c(G_m ⊗_k k, L_Ã(f(x)) ⊗L_χ)(1/2))

= √#E^–a–b det(Frob_E|H¹_c(G_m ⊗_k k, L_Ã(f(x)) ⊗L_χ)).

We follow the method of Hasse-Davenport [D-H]. The L-function on G_m/E with coefficients in L_Ã(f(x)) ⊗L_χ has the additive expression

where the inner sum is over the space of effective divisors of degree d on G_m/E. Concretely, the effective divisors D of given degree d are the monic polynomials of degree d in E[x] of the form f_D := x^d – s₁x^d–1 + …+ (–1)^ds_d, with s_d invertible. The term χ(D) for this divisor is χ(s_d). The term Ã(D) for this divisor is Ã(∑^a_i=–b A_iN_i), for N_i the sum of the i’th powers of the roots of the corresponding polynomial f_D. [N.B. Because f_D has an invertible constant term, all its roots are invertible, so N_i makes sense for negative i as well.] Comparing the additive expression for the L-function with its cohomological expression

L(G_m/E, T, L_Ã(f(x))⊗L_χ) = det(1–TFrob_E|H¹_c(G_m⊗_kk, L_Ã(f(x))⊗L_χ)),

which shows the L function to be a polynomial in T of degree a + b, and equating coefficients of T^a+b, we get the identity

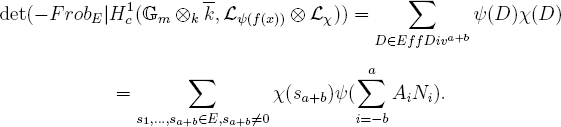
With the convention that for i > 0, s_–i is the i’th elementary symmetric function of the inverses of the roots, we have

s_–i = s_{a+ b–i} ∕s_{a+ b}.

And by the relation between Newton symmetric functions and elementary symmetric functions, we have

N_a = (–1)^{a+ 1}as_a + p_a(s₁, …, s_a–1),

where p_a(s₁, …, s_a–1) is isobaric of weight a and does not involve s_a. Similarly,

N_–b = (–1)^{b + 1}bs_–b + p_b(s_–1, …, s_–(b–1)),

where p_b(s_–1, …, s_–(b–1))is isobaric of weight b and does not involve s_–b. The terms N_i with 0 ≤ i < a are polynomials in the variables s₁, …, s_i, and the terms N_–j with 0 < j < b are polynomials in s_–1, …, s_–j. Thus we get an expression for

det(–Frob_E|H¹_c(G_m ⊗_k k, L_Ã(f(x)) ⊗L_χ)

of the form

with

R := P (s₁, …, s_a–1)+ Q(s_–1, …, s_–(b–1)).

Making use of the relations s_–i = s_a+b–i/s_{a+ b}, we see that the term Q(s_–1, …, s_–(b–1)) is itelf a polynomial in s_{a+ b–1}, s_{a+ b–2}, …., s_{a+ 1} and 1/s_{a+ b}. Thus R does not involve the variable s_a. Using the relation s_–b = s_a/s_{a+ b}, we see that the only occurrence of the variable s_a is in the two terms

A_a(–1)^{a+ 1}as_a + A_–b(–1)^{b+ 1}bs_a/s_{a+ b}.

So we can factor out the sum over s_a, and get an expression of det(–Frob_E) as the product of

times

This last sum vanishes unless

s_{a+ b} = A_–b(–1)^{b+ 1}b/A_a(–1)^aa,

in which case this sum is equal to #E. Defining α = A_–b(–1)^{b+ 1}b/A_a(–1)^aa, we get an expression for det(–Frob_E) as

χ(α) × (an expression independent ofχ).

Putting this all together, we get

det(–Frob_E,χ|!(N)) = χ(α)S(E, N)

with S(E, N) the exponential sum in a+ b–2 variables s₁, …, s_a–1, s_{a+ 1}, …, s_{a+ b–1} given by

Taking χ = , we see that

S(E, N) = det(–Frob_E, |!(N)).

Thus we find

det(Frob_E,χ|!(N)) = χ(α)det(Frob_E,|!(N)),

so defining

β := det(Frob_k, |!(N)),

we get the arithmetic determinant formula

“det”(N) = β^deg ⊗ δ_α.

 

The following lemma gives us some control over the quantity β := det(Frob_k, |!(N)).

Lemma 21.2. Let k be a finite field of characteristic p, Ã a nontrivial additive character of k. Let f(x) = ∑^a_i=–bA_ixⁱ ∈ k[x, 1/x] be a Laurent polynomial of “bidegree” (a, b), with a, b both ≥ 1 and both prime to p. The ratio

det(Frob_k|H¹_c(G_m/k, L_Ã(f(x))))²/(#k)^{a+ b}

is a root of unity of order dividing 2p if p is odd, and the ratio is ±1 if p = 2. If a + b is even, the same is true for the ratio

det(Frob_k|H¹_c(G_m/k, L_Ã(f(x))))/(#k)^{(a+ b)/2}.

If a + b is odd, the same is true of the ratio

det(Frob_k|H¹_c(G_m/k, L_Ã(f(x))))/(G(Ã, χ₂)(#k)^{(a+ b –1)/2}),

with G(Ã, χ₂) the quadratic Gauss sum.

Proof. The exponential sum expression for det(Frob_k|H¹_c(G_m/k, L_Ã(f(x)))) derived in the proof of the previous theorem shows that this determinant lies in the ring Z[ζ_p] of integers in the cyclotomic field Q(ζ_p). Hence the ratios in question all lie in Q(ζ_p) as well. We are asserting that the ratios in question are each roots of unity in Q(ζ_p). For this, it suffices to see that each ratio has absolute value one at every place, finite or infinite, of Q(ζ_p). At archimedean places, this is the fact that H¹_c(G_m/k, L_Ã(f(x))) is pure of weight one, and of dimension a + b. At ℓ-adic places, ℓ≠ p, both the determinant, calculated now via ℓ-adic cohomology, and the quantities #k and G(Ã, χ₂), are ℓ-adic units. At the unique place lying over p, both this determinant and its complex conjugate have the same p-adic absolute value as each other, as the two quantities are Galois conjugate in Q_p(ζ_p). But the two groups H¹_c(G_m/k, L_Ã(f(x))) and H¹_c(G_m/k, L_Ã(f(x))) are dually paired to Q_ℓ(–1), so the product of the determinant with its complex conjugate is (#k)^{a + b}. Therefore the square of the determinant, divided by (#k)^{a + b}, is a p-adic unit as well. The square of either of the second two ratios is ±1 times the first ratio, so it too is a p-adic unit.

Theorem 21.3. We have the following results concerning the object N of Theorem 21.1.

(1) The quantity

β := det(Frob_k, |!(N))

is a root of unity of order dividing 2p, if either a + b is even or if p is odd and –1 is a square in k. If p and a + b are both odd and –1 is a nonsquare in k, then β is a root of unity of order dividing 4p.

(2) If (–1)^aaA_a = (–1)^{b + 1}bA_–b, then for any a + b’th root ° of 1/β, the object °^deg ⊗ N has G_geom ⊂ G_arith ⊂ SL(a + b).

(3) If in addition a ≠ b and gcd{i|A_i ≠ 0} = 1 and a+ b is a prime number ≥ 3, then the object °^deg ⊗ N has G_geom = G_arith = SL(a + b).

(4) If the object °^deg ⊗ N has G_geom = G_arith = SL(a + b) (e.g., if a+ b is prime), then for any r ≥ 2 distinct characters χ₁, …, χ_r of k^×, the object ⊕^r_i=1°^deg ⊗ N ⊗ L_χi has

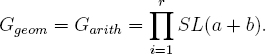
Proof. Assertion (1) is immediate from the corollary, because G(Ã, χ₂)² = χ₂(–1)#k. Assertion (2) is immediate from assertion (2) of Theorem 21.1. To prove (3), we argue as follows. By parts (3) and (4) of Theorem 21.1, G⁰_geom is an irreducible subgroup of SL(a + b) which lies in no orthogonal subgroup SO(a + b). By Gabber’s theorem on prime-dimensional representations [Ka-ESDE, 1.6], the only connected irreducible subgroups of SL(a+ b), for a+ b prime, are SL(a+ b), SO(a+ b), the image of SL(2) in Sym^{a+ b –1}(std₂), and, if a+ b = 7, the group G₂ in its seven-dimensional representation. All of these except for SL(a + b) itself lie in an orthogonal subgroup SO(a + b).

Assertion (4) results from the Goursat-Kolchin-Ribet Theorem 13.5. We have a priori inclusions for this object

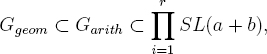
so it suffices to show that G_geom =∏^r_i=1 SL(a + b). We must show that for i ≠ j, and for any one-dimensional object L ∈ P_geom, there is no geometric isomorphism between N ⊗ L_χi and either N ⊗ L_χj ?_mid L or its Tannakian dual. To see this, we argue as follows. The fact that N ⊗ Lχ_i and N ⊗ L_χj and its Tannakian dual all have trivial determinants forces L^{⊗(a+ b)} to be geometrically trivial, which in turn implies that L is punctual, so some δ_² with² ∈ . Thus we must show that LÃ(f(x)) ⊗L_χi is not geometrically isomorphic to either L_Ã(f(²x)) ⊗L_χj or to L_{Ã(–f(²/x))} ⊗ L_χj, for any ². The second is impossible, because of the asymmetry of the Swan conductors. For the first, their ratio is LÃ(f(²x)–f(x)) ⊗L_χj/_χi. If ² ≠ 1, this ratio is wildly ramified at either 0 or ∞ or both, thanks to the hypothesis that f is Artin-Schreier reduced and has gcd{i|A_i ≠ 0} = 1. So their ratio is not geometrically trivial. If ² = 1, their ratio is L_χj/χi, which is nontrivially ramified at both 0 and ∞, so again is not geometrically trivial.

To end this chapter, we give another family of examples where, for every n ≥ 3 we have G_geom ⊂ G_arith ⊂ SL(n), but where, once again, only when n is prime can we prove that G_geom = G_arith = SL(n). We work over a finite field k, with à a nontrivial additive character of k. For each integer m ≥ 1, we denote by Kl_m the Kloosterman sheaf of rank m Kl_m(Ã; , , …, ). Recall that its complex conjugate Kl_m is given by Kl_m = [x (–1)^mx] ^?Kl_m.

Theorem 21.4. Fix strictly positive integers a ≠ b. Denote by F the lisse sheaf on G_m given by

F := Kl_a ⊗ [x 1/x] ^? Kl_b = Kl_a ⊗ [x (–1)^b/x] ^?Kl_b.

Denote by N ∈ P_arith the object F((a + b – 1)/2)[1]. Then we have the following results.

(1) The object N ∈ P_arith is pure of weight zero, geometrically irreducible, and of “dimension” a + b.

(2) For a multiplicative character χ of k^×, consider the Kloosterman sheaf Kl_{a+ b}(Ã; χ,.., χ, , …, ) of rank a + b with characters χ repeated a times, and repeated b times. Then we have the identity

det(1 – TFrob_k,χ|!(N))

= det(1 – TFrob_k,(–1)b |Kl_{a+ b}(Ã; χ,.., χ, , …, )((a + b – 1)/2)).

(3) We have G_geom,N ⊂ G_arith,N ⊂ SL(a + b).

(4) The object N ∈ P_arith is geometrically Lie-irreducible, i.e., G⁰_{geom, N} is an irreducible subgroup of SL(a + b).

(5) The object N ∈ P_arith is not geometrically Lie-self-dual, i.e., G⁰_{geom, N} lies in no orthogonal group SO(a + b) and, if a + b is even, it lies in no symplectic group Sp(a + b).

(6) If a + b is a prime number, then G_geom = G_arith = SL(a + b).

(7) Suppose that G_geom = G_arith = SL(a + b), and that gcd(a, b) = 1 (e.g., both hold if a + b is prime). For any r ≥ 2 distinct characters χ₁, …, χ_r of k^×, put N_i := N ⊗ L_χi. Then the object ⊕^r_i=1N_i has

Proof. (1) One knows that Kl_m is pure of weight m – 1, so F is pure of weight a + b – 2, and hence N is pure of weight zero. To show that N, or equivalently F, is geometrically irreducible, we repeat the argument given in Remark 18.14. By purity, F is geometrically semisimple, so it suffices to observe that its local monodromy at 0 (or at ∞, either one will do) is indecomposable. Its local monodromy at 0 is Unip(a) ⊗ Wild_b,1, where Wild_b,1 is totally wild of rank b and Swan conductor one, and the indecomposability follows from [Ka-RLS, 3.1.7]. Its local monodromy at ∞ is Wild_a,1 ⊗ Unip(b). Thus the dimension of N is Swan₀ + Swan_∞ = a + b.

To prove (2), it suffices to prove, over all finite extensions of k, the identity of traces

Trace(Frob_k,χ|!(N)) = Trace(Frob_k,(–1)b |Kl_{a+ b}(Ã; χ,.., χ, , …, )((a+ b–1)/2)).

Because F is totally wild at both 0 and ∞, there are no bad characters, so we have

Trace(Frob_k,χ|!(N)) := Trace(Frob_k|H⁰_c(G_m ⊗ k, N ⊗ L_χ))

= Trace(Frob_k|H¹_c(G_m ⊗ k, F ⊗L_χ)((a + b – 1)/2)).

So what we must show is the identity

Trace(Frob_k|H¹_c(G_m ⊗ k, F ⊗L_χ))

= Trace(Frob_k,(–1)b |Kl_{a+ b}(Ã; χ,.., χ, , …, )).

On the left-hand side, the H¹_c is the only nonvanishing cohomology group, so by the Lefschetz trace formula [Gr-Rat] the left-hand side is

This in turn is

which is precisely the trace of Frob_k,(–1)b on the convolution of Kl_a(Ã; χ, …, χ) with Kl_b, and that convolution is precisely the Kloosterman sheaf |Kl_{a+ b}(Ã; χ,.., χ, , …, ), cf. [Ka-GKM, 5.5].

To prove (3), it suffices to prove, thanks to (2), that for every χ we have the identity

det(Frob_k,(–1)b |Kl_{a + b}(Ã; χ,.., χ, , …, )) = (#k)^{(a+ b)(a+ b–1)/2}.

This identity is a special case of the arithmetic determinant formula for Kloosterman sheaves given in [Ka-GKM, 7.4.1.3 and 7.4.1.4]. [There the formula comes out as(#k)^{(a+ b)(a+ b–1)/2} times the additional factor χ^a((–1)^{a+ b–1)}χ^a((–1)^b), but this factor is 1.]

To prove (4), we must show that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. But already this is true for its local monodromy at 0, Unip(a) ⊗ Wild_b,1, indeed it is true for Wild_b,1 itself, cf. [Ka-GKM, 4.1.6 (3)].

We prove (5) exactly as in Theorem 21.1. We simply observe that N has different Swan conductors a and b at 0 and ∞ respectively, as do all its direct images by Kummer maps.

We then get (6) by Gabber’s classification of prime-dimensional representations [Ka-ESDE, 1.6], exactly as in the proof of Theorem 21.3.

To prove (7), we use Goursat-Kolchin-Ribet. We have a priori inclusions for the object ⊕^r_i=1N_i,

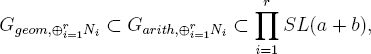
so it suffices to show that G_geom,⊕^r_i=1N_i = ∏^r_i=1 SL(a + b). We must show that for i ≠ j, and for any one-dimensional object L ∈ P_geom, there is no geometric isomorphism between N ⊗ L_χi and either (N ⊗ Lχ_j) ?_mid L or its Tannakian dual. To see this, we argue as follows. The fact that N ⊗ L_χi and N ⊗ L_χj and its Tannakian dual all have trivial determinants forces the Tannakian tensor power L^{⊗(a+ b)} to be geometrically trivial, which in turn implies that L is punctual, so some δ² with² ∈ . Thus we must show that for i ≠ j, N ⊗ L_χi is not geomerically isomorphic to any multiplicative translate of either N ⊗ Lχ_j or of its Tannakian dual. The second is impossible, because of the asymmetry of Swan conductors. To rule out the first, we argue as follows. If N ⊗ L_χi is geometrically isomorphic to some multiplicative translate [x ²x] ^?(N ⊗ L_χj), then comparing local monodromies at 0 and ∞ respectively we find geometric isomorphisms

Wild_b,1 ⊗L_χi ≅ [x ²x] ^?(Wild_b,1 ⊗L_χj)

and

Wild_a,1 ⊗L_χi ≅ [x x] ^?(Wild_a,1 ⊗L_χj).

Suppose first that a = 1. Then Wild_a,1 ≅ L_Ã(x) as I(∞) representation, so the second isomorphism asserts that L_Ã(x) ⊗L_χi ≅ L_Ã(²x) ⊗L_χj as I(∞) representation, i.e., that L_{Ã((1–²)x)} ⊗L_χi/χj is the trivial character of I(∞). This is nonsense: if² ≠ 1, this character has Swan conductor one, and if ² = 1, it is the nontrivial character L_χi/χj. Similarly, we deal with the case b = 1.

If both a, b ≥ 2, then both Wild_a,1 and Wild_b,1 have trivial determinants. Equating determinants in the two isomorphisms, we find equalities χ^b_i = χ^b_j and χ^a_i = χ^a_j. As gcd(a, b) = 1, we infer that χ_i = χ_j, contradiction.