CHAPTER 28

The Situation over Z: Results

Suppose we are given an integer monic polynomial f (x) ∈ Z[x] of degree n ≥ 2 which, over C, is “weakly supermorse,” meaning that it has n distinct roots in C, its derivative f ′ (x) has n – 1 distinct roots (the critical points) α_i ∈ C, and the n – 1 values f (α_i) (the critical values) are all distinct in C. Denote by S the set of critical values. Suppose that S is not equal to any nontrivial multiplicative translate aS, for any a ≠ 1 in C^×. It is standard that for all but finitely many primes p, the reduction mod p of f will satisfy all the hypotheses of Theorem 17.6. Let us say such a prime p is good for f.

Choose a prime, ℓ and a field isomorphism ι : Q ≅ C. For each p ≠ which is good for f, form the sheaf

F_p := f_? Q_ℓ/Q_ℓ|G_m/F_p,

and the corresponding object N_p := F_p(1/2)[1] ∈ P_arith on G_m/F_p, which is pure of weight zero, geometrically irreducible, and has

G_geom,Np = G_arith,Np = GL(n – 1).

We take the unitary group U(n – 1) as the compact form of GL(n – 1). For good p, the set of bad characters in this mod p situation is the set of characters of order dividing n. So for each good prime p ≠ ℓ, and for each character χ of F^×_p with χⁿ ≠ , we have the conjugacy classθ_Fp,χ ∈ U(n – 1)^#.

Emanuel Kowalski asked if, as p grew, the sets of conjugacy classes

{θ_Fp,χ}_{χ char of F^×p, χⁿ ≠1}

became equidistributed in the space U(n – 1)^# of conjugacy classes of U(n – 1). We will show that this, and more general things of the same flavor, are true.

Here is the general setup. We fix a prime, ℓ a field isomorphism ι : Q_ℓ ≅ C, a reductive group G over Q_ℓ, an integer n ≥ 1, and a faithful n-dimensional representation of G, i.e., an inclusion G ⊂ GL(n). We also fix a compact form K of G(C).

We also fix a sequence of finite fields k_i, each of characteristic ≠l, whose cardinalities are nondecreasing and tend archimedeanly to ∞. Thus for example the k_i could be successively higher degree extensions of a given prime field F_p with p = ℓ, or the k_i could be a sequence of prime fields F_pi with some increasing sequence of primes p_i > ℓ, or it could be the sequence of residue fields of the closed points of some flat scheme of finite type over Z[1/ℓ ], e.g., the spectrum of some O_K[1/nℓ ] for some number field K and some integer n ≠ 1, or the sequence of finite fields k_i could be any amalgam of these example situations.

Theorem 28.1. Suppose we are given, for each i, a form G_i/k_i of G_m/k_i, and an arithmetically semisimple object N_i in P_arith on G_i/k_i which is ι-pure of weight zero, and of “dimension” n. Suppose that for every i we have

G_geom,Ni = G_arith,Ni = G,

in such a way that the given n-dimensional representation of G, viewed as an n-dimensional representation of G_arith,Ni, corresponds to the object N_i. Suppose further that there exists a real number C ≥ n such that, for all i, we have both

gen.rk(N_i) ≤ C,

and

#Bad(N_i) ≤ C.

Then the sets Θ_i of conjugacy classes in K^#

Θ_i := {θ_ki,χ}_{χ char of Gi(ki), χ∈Good(ki,Ni)}

become equidistributed in K^# as #k_i → ∞.

Proof. Fix an irreducible nontrivial representation Λ of G. For each i, Λ corresponds to an object M_i in <N_i>_arith. We must show the large i limit of the averages

is zero.

Because G ⊂ GL(V) is reductive, the irreducible nontrivial representation Λ occurs in some tensor space V^⊗a ⊗ (V^∨)^⊗b, for some pair (a, b) of nonnegative integers. Of course the pair (a, b) is not unique. Nonetheless, let us fix one such pair, say with a + b minimal, for our given Λ. We will show that as soon as #k_i ≥ (1 + C)², we have the explicit bound

Recall from Remark 7.5 the explicit estimate (applied here with N = N_i and E = k_i, and valid as soon as C ≤ √#k_i – 1)

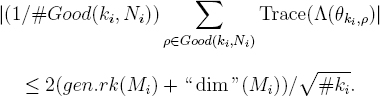
Since M_i is a direct summand of the tensor product in the Tannakian sense N^⊗a_i ⊗ (N^∨_i)^⊗b, we certainly have

“dim”(M_i) ≤ “dim”(N^⊗a_i ⊗ (N^∨_i)^⊗b) = n^a+b ≤ C^a+b

and

gen.rk(M_i) ≤ gen.rk(N^⊗a_i ⊗ (N^∨_i)^⊗b).

So it is sufficient to establish the inequality

gen.rk(N^⊗a_i ⊗ (N^∨_i)^⊗b) ≤ (a + b)C^a+b.

This in turn is a consequence of the inequality

gen.rk(N^⊗a_i ⊗ (N^∨_i)^⊗b) ≤ (a + b)(“dim”(N_i))^a+b–1gen.rk(N_i).

This inequality results, by induction on a+b, from the following general inequality, which will be proven below. Over any algebraically closed field of characterstic p ≠ ℓ, given two geometrically semisimple objects N and M in P_geom, we claim that we have the inequality

gen.rk(N?_mid M) ≤ “dim”(N)gen.rk(M)+ gen.rk(N)“dim”(M).

Indeed, if we grant this general inequality, then if a ≥ 1 we get

gen.rk(N^⊗a_i ⊗ (N^∨_i)^⊗b)

= gen.rk(N?_mid (N_i^⊗a–1 ⊗ (N^∨_i)^⊗b))

≤ “dim”(N_i)gen.rk(N_i^⊗a–1 ⊗(N^∨_i)^⊗b)+gen.rk(N_i)“dim”(N _i^⊗a–1 ⊗(N^∨_i)^⊗b).

By induction on a + b, we have

gen.rk(N_i^⊗a–1 ⊗ (N^∨_i)^⊗b) ≤ (a + b – 1)“dim”(N_i))^a+b–2gen.rk(N_i),

so we get the inequality

gen.rk(N^⊗a_i ⊗ (N^∨_i)^⊗b) ≤ (a + b)“dim”(N_i))^a+b–1gen.rk(N_i)

as asserted. If a = 0, we repeat this argument, “factoring out” one N^∨_i and doing induction on b.

We now establish the inequality used in the proof of Theorem 28.1. Because the function N “dim”(N) is multiplicative, i.e., “dim”(N?_mid M) = “dim”(N)“dim”(M), it is as though the inequality asserts a (sub)product formula for “differentiation,” where the function N gen.rk(N) plays the role of the “derivative” of the “dim” function.

Theorem 28.2. Over an algebraically closed field k of characterstic p ≠ ℓ, given two objects geometrically semisimple N and M in P_geom, we have the inequality

gen.rk(N ?_mid M) ≤ “dim”(N)gen.rk(M)+ gen.rk(N)“dim”(M).

Proof. Since all the terms in the asserted inequality are bilinear in the arguments N and M, we reduce immediately to the case where N and M are both geometrically irreducible.

If either N or M is punctual, say N = δ_a, then N ?_mid M is just the multiplicative translate [x ax] _? M = [x x/a]? M of M by a, so has the same generic rank as M. But “dim”(N) = 1, and gen.rk(N) = 0, so in this case we have equality.

Suppose now that our two objects in P_geom are each (geometrically irreducible, but we will not use this) middle extension sheaves placed in degree –1, say N = F[1] and M = G[1]. In this case, we first use the fact that N?_mid M is a quotient of N?_! M, so we have the trivial inequality

gen.rk(N?_mid M) ≤ gen.rk(N?_! M).

So it suffices to show the inequality

gen.rk(N?_! M) ≤ “dim”(N)gen.rk(M)+ gen.rk(N)“dim”(M).

Over a dense open set U ⊂ G_m/k, N?_! M|U is of the form H[1] for the lisse sheaf on U whose stalk at a point a ∈ U is the cohomology group H¹_c(G_m/k, F ⊗ [x a/x] ^?G), and this H¹_c is the only nonvanishing cohomology group. So for any a ∈ U(k), we have

gen.rk(N?_! M) = –χ(G_m/k, F ⊗ [x a/x] ^?g).

Shrinking U if necessary, we may further assume that for any point a ∈ U(k), the two middle extension sheaves F and [x a/x] ^?g on G_m have disjoint sets of ramification in G_m. Choose one point a ∈ U(k), and define

K := [x a/x] ^?g.

Then

“dim”(N) = –χ(G_m/k, F),

“dim”(M) = “dim”([x a/x]^?M) = –χ(G_m/k, K),

and

gen.rk(N?_! M) = –χ(G_m/k, F ⊗K).

So it suffices to prove that for two middle extension sheaves F and K on G_m/k with disjoint ramification, we have

–χ(G_m/k, F⊗K) ≤ –gen.rk(F)χ(G_m/k, K) – gen.rk(K)χ(G_m/k, F).

Now for any sheaf A on G_m/k, with ramification set Ram(A) ⊂ G_m, the Euler-Poincaré formula [Ray] gives

Taking A to be F ⊗ K, and denoting by S and T the disjoint ramification sets of F and of K, so that S ∪ T is the ramification set of A, we have (precisely because the ramification is disjoint)

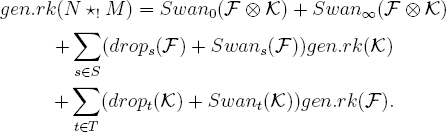
Let us admit for a moment the following two inequalities.

Swan₀(F ⊗K) ≤ Swan₀(F)gen.rk(K)+ Swan₀(K)gen.rk(F)

and

Swan_∞(F ⊗K) ≤ Swan_∞(F)gen.rk(K)+ Swan_∞(K)gen.rk(F).

Then we have the inequality

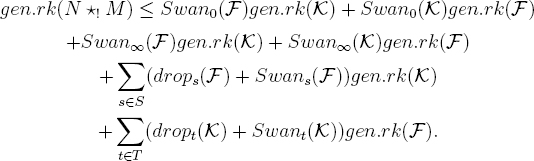
Factoring out the gen.rk(F) and gen.rk (K) terms, we see that this is precisely the inequality

gen.rk(N?_! M) ≤ “dim”(M)gen.rk(N) + “dim”(N)gen.rk(M).

So it remains to show that for two Q_ℓ-representations A and B of I(0), we have

Swan₀(A ⊗ B) ≤ Swan₀(A)rk(B)+ Swan₀(B)rk(A),

(and similarly for two Q_ℓ-representations of I(∞)).

Again by bilinearity, we may use the slope decomposition [Ka-GKM, Chapter 1] to reduce to the case where A and B each have only a single slope, say λ is the unique slope of A and μ is the unique slope of B, with say λ ≤ μ. Then I(0)^μ+ acts trivially on both A and B, so also trivially on A ⊗ B. Therefore all slopes of A ⊗ B are at most μ, so we have

Swan₀(A ⊗ B) ≤ μrk(A ⊗ B) = rk(A)μrk(B)

= Swan₀(B)rk(A) ≤ Swan₀(B)rk(A)+ Swan₀(A)rk(B).

Remark 28.3. How can one apply Theorem 28.1? Take for G one of the groups SL(n), GL(n), Sp(n), or a self-product of one of these groups, or O(2n). In Chapters 14, 15, 17, 18, 20, 21, 22, 23 and 24 we give various theorems which assert that a specific¹ N_i over a finite field k_i has G_geom,N_i = G_arith,N_i = G. Fix one such G, and choose one of the theorems in the relevant chapter. In all of these theorems, it happens that both the generic rank and the number of bad characters of the example object are bounded in terms of the “dimension” of that object. Given a sequence of finite fields k_i, each of characteristic ≠ ℓ, whose cardinalities are nondecreasing and tend archimedeanly to ∞, we have only to pick, for each i, an instance N_i over k_i of the chosen theorem, to have data to which Theorem 28.1 applies. Thus for example if we invoke Corollary 20.2 for some given value of r ≥ 1, we must first “throw way” those k_i of cardinality ≤ r, and for each of the remaining ones choose both a nontrivial additive character Ã_i of k_i and r distinct multiplicative characters of k^×_i. But there is no “compatiblity” of any kind required in these choices as k_i varies. Similarly, one way to invoke Theorem 17.6 is to start, as we did this chapter, with an integer monic polynomial f(x) ∈ Z[x] of degree n ≥ 2 which, over C, is “weakly supermorse,” and whose set S of critical values is not equal to any nontrivial multiplicative translate aS, for any a ≠ 1 in C^×. Then modulo sufficiently large primes p, the reduction mod p of f will satisfy all the hypotheses of Theorem 17.6. However, we could equally well invoke Theorem 17.6 by choosing separately for each (large) prime p a degree n monic polynomial f_p(x) ∈ F_p[x] to which the theorem applies.

Remark 28.4. In Chapter 19, which treats the orthogonal group, we only give situations where G_geom,Ni = SO(n) and G_arith,Ni ⊂ O(n), but no specific situations where we know that G_geom,Ni = G_arith,Ni =SO(n). But as we observed in Remark 19.13, in any such situation we will always achieve G_geom,Ni = G_arith,Ni = SO(n) after a quadratic extension of the ground field. So here we have the somewhat less optimal situation that if we pick one of the explicit example theorems of Chapter 19, then given our sequence of finite fields k_i, we pick for each an instance of that theorem, but only over the sequence of the quadratic extensions of the given k_i will we have data to which we can apply Theorem 28.1 with G taken to be SO(n).

¹The results of Chapters 25-27, devoted to G₂, fail to provide specific examples.