CHAPTER 18

Symplectic Examples

We work on either the split or the nonsplit form. We begin with a lisse sheaf F on a dense open set j : U ⊂ G which is geometrically irreducible, pure of weight zero, and not geometrically isomorphic to (the restriction to U of) any Kummer sheaf L_χ. Wedenoteby G := j_?F its middle extension to G. Then the object N := G(1/2)[1] ∈ P_arith is pure of weight zero and geometrically irreducible.

Theorem 18.1. Suppose that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself, and that N is symplectically self-dual. Suppose further that for either of the two possible geometric isomorphisms G/k ≅ G_m/k, both F(0)^unip and F(∞)^unip are a single Jordan block Unip(e) of the same size e ≥ 1. For n := dim(!(N)) we have

G_geom,N = G_arith,N = Sp(n).

Proof. We have a priori inclusions

G_geom,N ⊂ G_arith,N ⊂ Sp(n),

so it suffices to prove that G_geom,N = Sp(n). So we may extend scalars if necessary from k to its quadratic extension k₂, and reduce to the case where G is G_m. The hypothesis that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself insures that N is geometrically Lie-irreducible, i.e., that G⁰_geom is a connected irreducible subgroup of Sp(n). Thus G⁰_geom is semisimple: any connected irreducible subgroup of Sp(n) (indeed of SL(n)) is semisimple (it is reductive, because irreducible, and its center, necessarily consisting entirely of scalars by irreducibility, is finite).

The local monodromy of N at both 0 and ∞ is Unip(e). Therefore the semisimplification of Frob_k,1 gives us a Frobenius torus [Se-Let] Diag(x, 1/x, 1, …, 1) in G_arith,N. This torus normalizes the connected semisimple group G⁰_geom,N, and this group is an irreducible (in the given n-dimensional representation) subgroup of Sp(n). Take an element x₀ ∈ Q_ℓ^× which is not a root of unity. Then the element diag(x₀, 1/x₀, 1, …, 1) normalizes G⁰_geom,N. But a fixed power of any automorphism of a connected semisimple group is inner. So for some integer d ≥ 1, the element diag(x^d₀, 1/x^d₀, 1, …, 1) induces an inner auto-morphism of G⁰_geom,N, conjugation by some element ° ∈ G⁰_geom,N. Then °^–1diag(x^d₀, 1/x^d₀, 1, …, 1) commutes with every element of G⁰_geom,N, so is a scalar, say t ∈ Q_ℓ^×. Thus we find

diag(x^d₀, 1/x^d₀, 1, …, 1) = t°,

equality inside G_mG⁰_geom,N ⊂ GL(n). Both diag(x^d₀, 1/x^d₀, 1, …, 1) and ° have determinant one, so comparing determinants we see that tⁿ = 1, and hence

diag(x^nd₀, 1/x^nd₀, 1, …, 1) = °ⁿ

lies in G⁰_geom,N. As x₀ is not a root of unity, the entire torus Diag(x, 1/x, 1, …, 1) lies in G⁰_geom,N. By a beautiful result of Kostant and Zarhin [Ka-ESDE, 1.2], the only irreducible connected semisimple subgroups of SL(n) which contain the torus Diag(x, 1/x, 1, …, 1) are SL(n), SO(n), and, when n is even, Sp(n). Since we have an a priori inclusion G⁰_geom,N ⊂ Sp(n), we must have G⁰_geom,N = Sp(n). From the a priori inclusions G⁰_geom,N ⊂ G_geom,N ⊂ G_{arith,N ⊂} Sp(n), we get the asserted conclusion.

Here is a generalization of this last result.

Theorem 18.2. Suppose N satisfies all the hypotheses of the theorem above. Suppose further that

At either 0 or at ∞ or at both, the entire tame part of the local monodromy is Unip(e), i.e., local monodromy there is the direct sum of Unip(e) and of something totally wild.

Then for any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗L_χi have

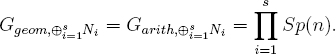
Proof. This is an immediate application of Theorem 13.1. As already noted, the operation M M ⊗ L_χi is a Tannakian isomorphism from <N>_arith to <N ⊗ L_χi>_arith, so each N_i has G_geom,Ni = G_arith,Ni = Sp(n). For i ≠ j, N_i and N_j have nonisomorphic tame parts of local monodromy at either 0 or at ∞ or at both, so they cannot be geometrically isomorphic. For the same reason, N_i is not geometrically isomorphic to [x –x] N_j; indeed N_j and [x –x]^? N_j have isomorphic tame parts of local monodromy at both 0 and ∞. [More generally, tame representations of either I(0) or of I(∞) are geometrically isomorphic to all their multiplicative translates.]

We now give some concrete examples. The first example is based on the Legendre sheaf Leg introduced in Chapter 15.

Theorem 18.3. Let k have odd characteristic. For any even integer n ≥ 2, the object N := Symⁿ(Leg)((n + 1)/2)[1] in P_arith is pure of weight zero, of “dimension” n, and has

G_geom,N = G_arith,N = Sp(n).

Proof. The lisse sheaf Leg(1/2)|A¹ {0, 1} has SL(2) as its geometric (and its arithmetic) monodromy group, so every symmetric power Symⁿ of it is geometrically irreducible and self-dual, orthogonally if n is even and symplectically if n is odd. Under multiplicative inversion, we have

[λ 1/λ]^? Leg ≅ Leg ⊗ L_χ2(λ).

Thus each even symmetric power of Leg(1/2)|A¹ {0, 1} is both orthogonally self-dual and invariant under multiplicative inversion. So the object N in P_arith is pure of weight zero, geometrically irreducible, and self-dual. Moreover it is geometrically Lie-irreducible, because the point 1 ∈ G_m(k) is its unique singularity. Its “dimension” is n; indeed it is everywhere tame, and at its unique singularity 1 ∈ G_m(k) its local monodromy is Unip(n + 1), so its drop is n. Let us admit for the moment that the autoduality of N is symplectic. Then we argue as follows. The local monodromy of N at both 0 and ∞ is Unip(n +1). Theorem 18.1 then gives the asserted conclusion.

It remains to show that N is symplectically self-dual. Because we know already that N is either symplectically or orthogonally self-dual, we may make a finite extension of the ground field to determine which. So replacing k by k₂ if necessary, we reduce to the case when k contains the fourth roots of unity. We will apply Theorem 11.2. Write the even integer n as n = 2d. We will show that the lisse sheaf Sym^2d(Leg)(d)|A¹ {0, 1} is the pullback, by λ λ +1/λ, of a lisse sheaf F_2d+1 on A¹ {2, –2} which is orthogonally self-dual, and whose G_geom,F2d+1 is the image of μ₄SL(2) in Sym^2d(std₂). [In this representation, SL(2) has image an irreducible subgroup of SO(2d + 1), while μ₄ acts trivially if d is even, and with scalar image ±1 if d is odd.] Then by Theorem 11.2 the autoduality on N is symplectic.

For the group SL(2), we recover Sym^2d(std₂) as the highest dimensional constituent of Sym^d(Sym²(std₂)). Indeed, by Hermite’s identity, we have Sym^d(Sym²(std₂)) ≅ Sym²(Sym^d(std₂)), and as already noted (in the paragraph preceding Theorem 11.2), we have

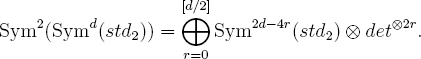
Now think of Sym²(std₂) as std₃ for SO(3). This group SO(3) has a unique irreducible representation V_2r+1 of each odd dimension 2r +1, namely Sym²r(std₂), when we think of SO(3) as SL(2)/±1. The above identity then is the statement that as representations of SO(3), we have

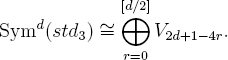
Consequently, we have

V_2d+1 ≅ Sym^d(std₃)/Sym^d–2(std₃).

[In other words, V_2d+1 as representation of SO(3) is the space of spherical harmonics of degree d on S².] Applying this to Leg(1/2) on A¹ {0, 1}, we get

Sym^2d(Leg)(d) ≅ Sym^d(Sym²(Leg)(1))/Sym^d–2(Sym²(Leg)(1)).

This reduces us to the case n = 2, i.e., to the problem of showing that Sym²(Leg)(1)|A¹ {0, 1} is arithmetically isomorphic to the pull-back, by λ λ+1/λ, of a lisse rank three sheaf F₃ on A¹{2, –2} which is orthogonally self-dual, with G_geom,F3 the group O(3) = ±SO(3), viewed as the image of μ₄SL(2) in Sym²(std₂). To do this, we may replace Leg by its quadratic twist TwLeg := Leg ⊗ L_χ2(1–λ), because for even n, Leg and TwLeg have the same Symⁿ.

To construct F₃, we will first exhibit a lisse, rank two sheaf H on A¹ {2, –2} such that TwLeg is geometrically the pullback of H by λ λ + 1/λ. This sheaf H is not self-dual, but we will show that Sym²(H) is self-dual, with G_{geom,Sym²(H)} the group O(3). Then we will take F₃ to be Sym²(H), or possibly its constant field quadratic twist (–1)^deg ⊗ Sym²(H).

For H, we start with the hypergeometric sheaf H(Ã; χ₄,χ₄; , )(3/2) of type (2, 2), with χ₄ a character of k^× of order 4. This sheaf is pure of weight zero, its local monodromy at 0 is L_χ4 ⊗ Unip(2), its local monodromy at 1 is ⊕ L_χ2, and its local monodromy at ∞ is Unip(2). Then [x (2 – x)/4] H(Ã; χ₄,χ₄; , )(3/2) is the desired H. Its local monodromy at ∞ is Unip(2), its local monodromy at 2 is L_χ4⊗ Unip(2), and its local monodromy at –2 is ⊕ L_χ2.

The pullback of this H by λ λ +1/λ has the same local monodromies as TwLeg, namely Unip(2) at 0 and ∞, and L_χ2 ⊗ Unip(2) at 1. The pullback is lisse at –1. By rigidity, the pullback is geometrically isomorphic to TwLeg. Therefore Sym²(TwLeg)(1)|A¹ {0, 1} is geometrically isomorphic to the pullback by λ λ +1/λ of

F₃ := Sym²(H) = [x → (2 – x)/4]^?Sym²(H(Ã; χ₄,χ₄; , ))(3).

Again by rigidity, Sym²(H(Ã; χ₄,χ₄; , ))(3) is geometrically isomorphic to the hypergeometric sheaf H(χ₂,χ₂,χ₂; , , )(5/2) of type (3, 3). This sheaf is orthogonally self-dual. We claim that its G_geom is O(3). Its local monodromy at ∞ is Unip(3), so I(∞), and a fortiori G⁰_geom, act indecomposably. Therefore G⁰_geom acts irreducibly (because by purity it acts semisimply). So G⁰_geom is a connected irreducible subgroup of SO(3), and the only such is SO(3) itself. On the other hand, det(H(χ₂,χ₂,χ₂; , , )(5/2)) is geometrically L_{χ2(x(1–x))}, so we have G_geom = O(3), as asserted.

So our situation is this. We have a lisse sheaf F₃ which is pure of weight zero, lisse of rank three, orthogonally self-dual with G_geom,F3 = O(3). Its pullback by λ λ+1/λ,callit K, is geometrically isomorphic to Sym²(TwLeg)(1). Since both Sym²(TwLeg)(1) and the pullback K are geometrically irreducible and arithmetically orthogonal, the space

Hom_geom(K, Sym²(TwLeg)(1))

is a one-dimensional orthogonal Gal(k/k)-representation, some α^deg, with α = ±1. We have an arithmetic isomorphism

K ⊗ Hom_geom(K, Sym²(TwLeg)(1)) ≅ Sym²(TwLeg)(1),

i.e., an arithmetic isomorphism K ⊗ α^deg ≅ Sym²(TwLeg)(1). Replacing F₃ by α^deg ⊗ F₃ if necessary, i.e., if α = –1, we get the required F₃.

Applying Theorem 18.2 to this N, we get the following result.

Theorem 18.4. For n ≥ 2 even, N := Symⁿ(Leg)((n + 1)/2)[1], and for any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗ L_χi have

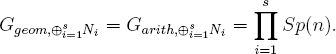
We now analyze the odd symmetric powers of the twisted Legendre sheaf TwLeg.

Theorem 18.5. Let k have odd characteristic and contain the fourth roots of unity. For any odd integer n ≥ 1, the object

N := Symⁿ(TwLeg)((n +1)/2)[1]

in P_arith is pure of weight zero, of “dimension” n +1, and has

G_geom,N = G_arith,N = Sp(n +1).

Proof. Because k contains the fourth roots of unity, the sheaf TwLeg and hence the object N is isomorphic to its pullback by multiplicative inversion. Just as in the start of the proof of Theorem 18.3, we see that N is pure of weight zero, geometrically Lie-irreducible, and self-dual. Its local monodromy at both 0 and ∞ is Unip(n + 1). Its local monodromy at 1 is L_χ2 ⊗ Unip(n + 1), so its “dimension” is drop₁ = n +1. Exactly as in Theorem 18.3, it suffices to show that N is symplectically self-dual.

As already shown in the proof of Theorem 18.3, TwLeg is geometrically the pullback by π : λ λ +1/λ of the sheaf

H := [x (2 – x)/4]^? H(Ã; χ₄,χ₄; , )(3/2).

From the known local monodromies of H(Ã; χ₄,χ₄; , ), we see that det H(Ã; χ₄,χ₄; , )) is geometrically isomorphic to L_{χ2(x(1–x))}. Hence det(H) is geometrically isomorphic to [x (2 – x)/4]^? L_{χ2(x(1–x))} ≅ L_χ2(x²–4). Thus for some unitary scalar α, det(H) is arithmetically isomorphic to α^deg ⊗ L_χ2(x²–4).

Choose a square root β of 1/α, and put H₁ := β^deg ⊗H. This object H₁ has determinant L_χ2(x²–4) arithmetically, its pullback by π : λ λ +1/λ is geometrically isomorphic to TwLeg, and its determinant is arithmetically trivial:

det(π^?H₁) = π^? det(H₁) = π^? L_χ2(x²–4)

= L_{χ2((λ+1/λ)²–4)} = L_{χ2((λ–1/λ)²)} ≅ Q_ℓ.

Thus both π^?H₁ and TwLeg(1/2) are arithmetically symplectically self-dual (being of rank two and trivial determinant), geometrically irreducible, and geometrically isomorphic. So for some choice of ° = ±1, we have an arithmetic isomorphism

π^?(°^degH₁) ≅ = TwLeg(1/2).

Replacing H₁ by °^degH₁ if needed, we have an H₁ with arithmetic determinant L_χ2(x²–4), geometric monodromy μ₄SL(2), and an arithmetic isomorphism π^? H₁ ≅ TwLeg(1/2).

Now fix an odd integer n = 2d – 1 ≥ 1. Define the lisse sheaf F on G_m {±2} by

F := Sym^2d–1(H₁),

and the object N ∈ P_arith by

N := j_? π^? F(1/2)[1].

This N is just Symⁿ(TwLeg)((n +1)/2)[1]. The situation is reminiscent of that considered in Theorems 11.1 and 11.2, except that F is not geometrically self-dual. Indeed, the geometric monodromy group of F is μ₄SL(2), viewed in the representation Sym²d–1(std₂), a subgroup of GL(2d) which contains the scalars μ₄, hence lies in neither the orthogonal nor the symplectic group. Nonetheless, we will use the calculational method of the proof of Theorem 11.1 to determine the sign _N of the autoduality of N. In the notations of that theorem, where the “x” above becomes “s,” the sums whose large #E limit is – ²_N are

We next observe that because F is pure of weight zero, geometrically irreducible and not geometrically self-dual, we have the estimate

cf. [Ka-MMP, 1.9.6, assertion 1)]. Indeed, both the sheaves Sym²(F) and Λ²(F) have vanishing H²_c on U ⊗_k k, and their H¹_c’s are mixed of weight ≤ 1, so the estimate follows from the Lefschetz Trace formula [Gr-Rat] and the linear algebra identity

Trace(Frob_E2,s|F) = Trace(Frob_E,s|Sym²(F))–Trace(Frob_E,s|Λ²(F)).

So we are reduced to showing that the sums

are approximately –1. To see this, we make use of the linear algebra identity above. So it suffices to prove that the Sym² term

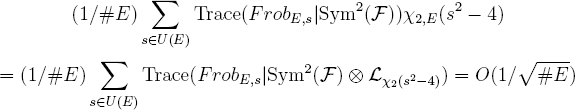
and that the Λ² term

is approximately 1.

We now use the fact that F = Sym^2d–1(H₁), with H₁ pureofweight zero, with geometric monodromy group μ₄SL(2) and with arithmetic determinant L_χ2(s²–4). Recall the identities for GL(2)-representations

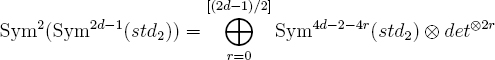
and

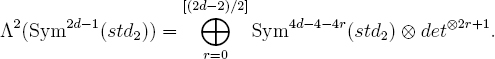
Applying these to H₁, we see every geometrically irreducible constituent of Sym²(F) has rank ≥ 3, which gives the asserted O(1/√#E) estimate for the Sym² sum. We also see that Λ²(F) is the direct sum of L_χ2(s²–4) with a complement, each of whose geometrically irreducible constituents has dimension ≥ 5. So this complement gives a sum which is O(1/√#E). The remaining term, the L_χ2(s²–4) sum, is

as required.

Exactly as for even symmetric powers, we can apply Theorem 18.2 to this N.

Theorem 18.6. For n ≥ 1 odd, N := Symⁿ(TwLeg)((n + 1)/2)[1], and for any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗ L_χi have

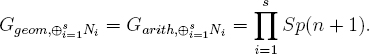
For the next example, we continue to work on G_m/k with k of odd characteristic. Recall that a polynomial f(x) = ∑^2g_i=0 a_ixⁱ ∈ k[x] of even degree 2g is said to be palindromic if a_g+i = a_g–i for 0 ≤ i ≤ g.

Theorem 18.7. Let 2g ≥ 2 be an even integer, and f(x) ∈ k[x] a palindromic polynomial of degree 2g. Suppose that f has 2g distinct roots in k, and that f is not a polynomial in x^d for any prime to p integer d ≥ 2. Denote by j : G_m[1/f] ⊂ G_m the inclusion. Then both of the objects

N := j_?L_χ2(f(x))(1/2)[1]

and

M := j_? L_χ2(xf(x))(1/2)[1]

in P_arith are geometrically irreducible, pure of weight zero, symplectically self-dual of “dimension” 2g, and have G_geom = G_arith = Sp(2g).

Proof. Since f is palindromic of degree 2g its constant term is nonzero. So all its 2g distinct zeroes lie in G_m(k). So both j_?L_χ2(f(x)) and j_?L_χ2(xf(x)) are irreducible middle extension sheaves on G_m, pure of weight zero and not geometrically isomorphic to any Kummer sheaf Lχ. So both M and N are geometrically irreducible objects of P_arith, pure of weight zero and of “dimension” 2g. We have

M = N ⊗ L_χ2.

So K K ⊗ L_χ2 is a Tannakian isomorphism from <N>_arith to <M>_arith. So N and M have the same groups G_geom as each other, and the same groups G_arith as each other.

Let us first show that N is geometrically Lie-irreducible, i.e., not geometrically isomorphic to any nontrivial multiplicative translate of itself. This amounts to the statement that j_?L_χ2(f(x)) = j_!L_χ2(f(x)) is not geometrically isomorphic to j_!L_{χ 2(f(ax))} for any a ≠ 1 in k^×. We argue by contradiction. Now j_!L_χ2(f(x)) has singularities precisely at the 2g zeroes of f(x), while j_!L_χ2(f(ax)) has singularities precisely at the 2g zeroes of f(ax). So if the two are geometrically isomorphic for some a ≠ 1 in k^×, then f(x) and f(ax) have the same zeroes. Therefore for some constant b ∈ k^×, we have f(ax) = bf(x). Comparing the nonzero constant terms, we see that b = 1, i.e., f(x) = f(ax). But for d > 1 the multiplicative order of a ∈ k^×, the equality f(x) = f(ax) implies that f(x) is a polynomial in x^d.

To see that N, or equivalently M, is symplectically self-dual, we remark that for any palindromic f(x) of degree 2g in k[x], f(x)/x^g is a palindromic Laurent polynomial of bidegree (–g, g) in k[x, 1/x], so there is a unique polynomial h_g(x) ∈ k[x] of degree g such that F(x)/x^g = h_g(x +1/x). Because f has 2g distinct zeroes, h_g must have g distinct zeroes, none of which is ±2. If g is even, then

j_?L_χ2(f(x)) = j_?L_{χ2(f(x)/x^g)} = j_?L_{χ2(hg(x+1/x))},

and we apply Theorem 11.1, with the orthogonally self-dual F = L_χ2(hg(x)), to conclude that N is symplectically self-dual. [This sheaf F = L_χ2(hg(x))has g distinct singularities in A¹, so at least g – 1 in G_m, so is not geometrically isomorphic to any Kummer sheaf L_χ.] If g is odd, then

j_?L_χ2(xf(x)) = j_?L_{χ2(f(x)/x^g)} = j_?L_{χ2(hg(x+1/x))},

and we conclude now by Theorem 11.1 that M is symplectically self-dual. [If g = 1, then the unique zero of h_g lies in G_m(k), for otherwise f(x) would be a constant multiple of 1 + x². So again in this case F = L_χ2(hg(x)) is not geometrically isomorphic to any Kummer sheaf L_χ.]

The local monodromies of N at 0 and at ∞ are both Unip(1) (be-cause f is invertible at 0 and has even degree), so exactly as in the proof of the previous theorem, Frob_k, gives rise to a Frobenius torus Diag(x, 1/x, 1, …, 1) in G⁰_geom,N, which is an irreducible subgroup of Sp(2g). So again by the theorem of Kostant and Zarhin [Ka-ESDE, 1.2], we conclude that G⁰_geom,N = Sp(2g), which then forces G⁰_geom,N = G_geom,N = G_arith,N = Sp(2g).

Again here we can apply Theorem 18.2.

Theorem 18.8. For N := j_?L_χ2(f(x))(1/2)[1] satisfying all the hypotheses of Theorem 18.7, and for any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗ L_χi have

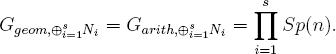
For the next example, we will apply Theorem 10.1. We continue to work on G_m/k.

Theorem 18.9. Choose a nontrivial character ρ of k^×, of order r > 2. Let f(x) ∈ k[x] be a polynomial whose degree rn is a multiple of r, such that

(1) f(x) has rn distinct zeroes in k^×.

(2) f(x) and f(1/x) have no common zeroes.

(3) f(x) is not a polynomial in x^d for any prime to p integer d > 1.

For j : G_m[1/f(x)f(1/x)] ⊂ G_m, the object N := j_?L_{ρ(f(x)/f(1/x))}(1/2)[1] in P_arith is geometrically irreducible, pure of weight zero, symplectically self-dual of “dimension” 2rn, and has G_geom = G_arith = Sp(2rn).

Proof. The object N in P_arith is geometrically irreducible, pure of weight zero, and of “dimension” 2rn. We next show that it is geometrically Lie-irreducible, i.e., not geometrically isomorphic to any nontrivial multiplicative translate of itself. We argue by contradiction. The object N has singularities precisely at the zeroes of f(x), where its local monodromy is L_ρ, and at the zeroes of f(1/x), where its local monodromy is L_ρ. Because ρ has order r ≥ 3, we recover the zeroes of f(x) as being the singularities where the local monodromy is L_ρ. So if multiplicative translation by some a ≠ 1 in k^× preserves the geometric isomorphism class of N, then f(x) and f(ax) have the same zeroes, so are proportional. Because f has a nonzero constant term, we must have f(ax) = f(x). Thus if a has multiplicative order d ≥ 2, then f(x) is a polynomial in x^d, contradiction.

To apply Theorem 10.1, take for F there the middle extension of L_ρ(f(x)). This shows that N is symplectically self-dual. By the geometric Lie-irreducibility of N, G⁰_geom,N ⊂ Sp(2rn) is a connected irreducible subgroup, so an irreducible connected semisimple subgroup. Because f has degree multiple of r, the order of ρ, the local monodromy of L_{ρ(f(x)/f(1/x))} at both 0 and ∞ is Unip(1), so exactly as in the proof of Theorem 18.1 we get a Frobenius torus Diag(x, 1/x, 1, …, 1) in G⁰_geom,N. Exactly as in the proof of Theorem 18.2, the theorem of Kostant and Zarhin [Ka-ESDE, 1.2] shows that G⁰_geom,N = Sp(2rn), which then forces G⁰_geom,N = G_geom,N = G_arith,N = Sp(2rn).

Remark 18.10. What becomes of the theorem above if we try to take for ρ the quadratic character χ₂? Thus f(x) has even degree 2d, and we are looking at L_{χ 2(f(x)/f(1/x))} = L_{χ2(f(x)f(1/x))} = L_{χ2(f(x)x^2df(1/x))} = L_{χ2(f(x)f^pal(x))}. This is a situation to which Theorem 18.2 would apply, to the palindromic polynomial f(x)f^pal(x) of degree 4d, provided that f(x)f^pal(x) is not a polynomial in x^e for any integer e > 1 prime to p. This condition is strictly stronger than the hypothesis that f(x) not be a polynomial in x^e for any integer e > 1 prime to p. For a simple example, take an f for which f^pal(x) = ±f(–x), e.g., f(x) = x²+bx–1 with b ≠ 0,b² +4 ≠ 0.

We can apply Theorem 18.2.

Theorem 18.11. For N := j_?L_{ρ(f(x)/f(1/x))}(1/2)[1] satisfying all the hypotheses of Theorem 18.9, and for any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗ L_χi have

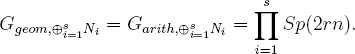
We next give an example based on hypergeometric sheaves. We work on G_m/k, with k of odd characteristic. We fix an odd integer 2k +1 ≥ 3, and we consider the hypergeometric sheaf of type (1, 2k +1)

H := H(Ã; χ₂; , …., )((2k +1)/2).

This H is lisse on G_m, pure of weight zero and orthogonally self-dual. Its local monodromy at ∞ is Unip(2k + 1). Its local monodromy at 0 is the direct sum

H(0) ≅ = L_χ2 ⊕ Wild_2k,

with Wild_2k totally wild of rank 2k and Swan conductor 1. This object is Lie-irreducible, and in fact one knows that both its G_geom and its G_arith are the full orthogonal group O(2k + 1). We next form the pullback π^? H of H by the finite map of degree 2

π : G_m {1} → G_m, x x +1/x – 2.

This covering (extended to a finite flat cover of P¹) is finite étale over ∞, with 0 and ∞ the two points in the source lying over it. The covering is doubly ramified over 0, with 1 the unique point in the source lying over it. It is also doubly ramified over –4, with –1 the unique point lying over. For j₁ : G_m {1} ⊂ G_m the inclusion, we form the object N ∈ P_arith given by

N := j_1?π^? H(1/2)[1].

This object is pure of weight zero and geometrically irreducible. It is symplectically self-dual, by Theorem 11.1. [View π^?H as the pullback by x x +1/x of the sheaf [x x – 2]^? H, and take the sheaf F of Theorem 11.1 to be the sheaf [x x – 2]^?H.]

Theorem 18.12. The object N ∈ P_arith is pure of weight zero, and has G⁰_geom,N = G_geom,N = G_arith,N = Sp(2k +2).

Proof. Because 1 is the unique singularity of N in G_m(k), N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Its local monodromy at both 0 and ∞ is Unip(2k + 1). Because 1 maps doubly to 0, its local monodromy at 1 is the direct sum of Unip(1) and of a totally wild part of rank 2k and Swan conductor 2. So its “dimension” is drop₁ + Swan₁ = 2k + 2. The result now follows from Theorem 18.1.

Applying Theorem 18.2 to N, we get the following.

Theorem 18.13. For any s ≥ 2 distinct characters χ₁, …, χ_s of G(k), the objects N_i := N ⊗ L_χi have

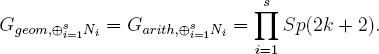
Remark 18.14. Here is a nagging open problem. Suppose we are given f(x) = ∑^d_i=0 A_ixⁱ ∈ k[x] a polynomial of degree d prime to p, which is Artin-Schreier reduced, i.e., A_i vanishes if p|i, and such that gcd{i|A_i ≠ 0} = 1. According to Theorem 10.1, the object N := L_{Ã(f(x)–f(1/x))}(1/2)[1] is symplectically self-dual. The gcd = 1 hypothesis, together with Artin-Schreier reducedness, insures that N is not geometrically isomorphic to any nontrivial multiplicative translate of itself, so N is Lie-irreducible. Because N is totally wildly ramified at both 0 and ∞, it has no bad characters χ. We believe that G_geom,N = Sp(2d), but in the absence of any bad characters χ, we are unable to prove it (except in the case d = 1, the Evans example, where there is a dearth of Lie-irreducible subgroups of SL(2), cf. Theorem 14.2).

This can be viewed as a special case of the following problem. Take for F a geometrically irreducible lisse sheaf F on G_m/k of rank n ≥ 1 which is pure of weight zero, whose I(0)-representation is Unip(n), and whose I(∞)-representation is totally wild, say of Swan conductor k ≥ 1, and both irreducible and not geometrically isomorphic to any nontrivial multiplicative translate of itself. Denote by F its “complex conjugate,” i.e., its linear dual, and form the lisse sheaf

G := F ⊗ ([x 1/x] F).

Then the local monodromy of G at both 0 and ∞ is of the form Unip(n) ⊗ Wild_n,k, where Wild_n,k is irreducible of rank n and Swan conductor k, and not isomorphic to any nontrivial multiplicative translate of itself. It follows [Ka-RLS, 3.1.7] that each of these local monodromies is indecomposable. From this indecomposability, it follows that G is indecomposable. But F is itself geometrically irreducible and hence geometrically semisimple, so G, as the tensor product of two geometrically semisimple lisse sheaves, is itself geometrically semisimple. [Alternatively, G is geometrically semisimple because it is pure of weight zero.] Being indecomposable as well, G is geometrically irreducible. Looking at its I(∞)-representation, we see that G is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Thanks to Theorem 10.1, we know that the object N := G(1/2)[1] is symplectically self-dual. Its “dimension” is 2nk. Is it always the case that G_geom,N = Sp(2nk), or does one need to impose additional conditions on F?

Let us consider the special case when F is a Kloosterman sheaf Kl_n := Kl_n(Ã; , …, )((n – 1)/2). One knows [Ka-GKM, 4.1.1 (3)] that the I(∞)-representation of Kl_n is totally wild, of Swan conductor one, and (consequently, cf. [Ka-GKM, 4.1.6 (3)]) is not geometrically isomorphic to any nontrivial multiplicative translate of itself. Its I(0)-representation is Unip(n). Is it true that for the associated N, we have G_geom,N = Sp(2n)? This seems to be an open question, except for the case n = 1, where we once again find the Evans example.

We end this chapter with an example inspired by that of Rudnick, cf. Theorem 14.5.

Theorem 18.15. Let k be a finite field of odd characteristic, f(x) ∈ k[x] an odd polynomial (i.e., f(–x) = –f(x)) of prime-to-p degree 2n – 1. Denote by j₁ : G_m {1} G_m the inclusion. Then the object N := j_1?L_{Ã(f((x+1)/(x–1)))}(1/2)[1] ∈ P_arith is pure of weight zero and has G_geom,N = G_arith,N = Sp(2n).

Proof. The lisse sheaf L_{Ã(f((x+1)/(x–1)))} on G_m {1} is wildly ramified at the point 1, with Swan conductor 2n – 1, so is not geometrically isomorphic to any L_χ. Thus N is geometrically irreducible, being a middle extension of generic rank one. Because g(x) := f((x+1)/(x–1)) satisfies g(1/x) = –g(x), we can write g(x) = (1/2)g(x) – (1/2)g(1/x), and then apply Theorem 10.1 to see that N is symplectically self-dual. As the unique singularity of N is at the point 1, N is not geometrically isomorphic to any nontrivial multiplicative translate of itself. As N is lisse at both 0 and ∞, and of generic rank one, the result now follows from Theorem 18.1.

Applying Theorem 18.2, we get the following generalization of this last result.

Theorem 18.16. For the object N of the previous theorem, and any r ≥ 1 distinct multiplicative characters χ₁, …, χ_r of k^×, define N_i := N ⊗ L_χi. Then the object ⊕_iN_i has G_geom,⊕iNi = G_arith,⊕iNi = Sp(2n).