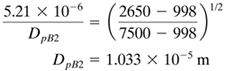14.3. SETTLING AND SEDIMENTATION IN PARTICLE–FLUID SEPARATION

14.3A. Introduction

In filtration, the solid particles are removed from the slurry by forcing the fluid through a filter medium, which blocks the passage of the solid particles and allows the filtrate to pass through. In settling and sedimentation, the particles are separated from the fluid by gravitational forces acting on the particles.

Applications of settling and sedimentation include removal of solids from liquid sewage wastes, settling of crystals from the mother liquor, separation of liquid–liquid mixture from a solvent-extraction stage in a settler, settling of solid food particles from a liquid food, and settling of a slurry from a soybean leaching process. The particles can be solid particles or liquid drops. The fluid can be a liquid or gas and it may be at rest or in motion.

In some processes of settling and sedimentation, the purpose is to remove the particles from the fluid stream so that the fluid is free of particle contaminants. In other processes, the particles are recovered as the product, as in recovery of the dispersed phase in liquid–liquid extraction. In some cases the particles are suspended in fluids so that the particles can be separated into fractions differing in size or in density.

When a particle is at a sufficient distance from the walls of the container and from other particles so that its fall is not affected by them, the process is called free settling. Interference is less than 1% if the ratio of the particle diameter to the container diameter is less than 1:200 or if the particle concentration is less than 0.2 vol % in the solution. When the particles are crowded, they settle at a lower rate and the process is called hindered settling. The separation of a dilute slurry or suspension by gravity settling into a clear fluid and a slurry of higher solids content is called sedimentation.

14.3B. Theory of Particle Movement Through a Fluid

1. Derivation of basic equations for rigid spheres

Whenever a particle is moving through a fluid, a number of forces will be acting on the particle. First, a density difference is needed between the particle and the fluid. An external force of gravity is needed to impart motion to the particle. If the densities of the fluid and particle are equal, the buoyant force on the particle will counterbalance the external force and the particle will not move relative to the fluid.

For a rigid particle moving in a fluid, there are three forces acting on the body: gravity acting downward, buoyant force acting upward, and resistance or drag force acting in opposite direction to the particle motion.

We will consider a particle of mass m kg falling at a velocity ν m/s relative to the fluid. The density of the solid particle is ρ_p kg/m³ solid and that of the liquid is ρ kg/m³ liquid. The buoyant force F_b in N on the particle is

Equation 14.3-1

where m/ρ_p is the volume V_p in m³ of the particle and g is the gravitational acceleration in m/s².

The gravitation or external force F_g in N on the particle is

Equation 14.3-2

The drag force F_D on a body in N may be derived from the fact that, as in flow of fluids, the drag force or frictional resistance is proportional to the velocity head ν²/2 of the fluid displaced by the moving body. This must be multiplied by the density of the fluid and by a significant area A, such as the projected area of the particle. This was defined previously in Eq. (3.1-1):

Equation 14.3-3

where the drag coefficient C_D is the proportionality constant and is dimensionless.

The resultant force on the body is then F_g − F_b − F_D. This resultant force must equal the force due to acceleration:

Equation 14.3-4

Substituting Eqs. (14.3-1)–(14.3-3) into (14.3-4),

Equation 14.3-5

If we start from the moment the body is released from its position of rest, the falling of the body consists of two periods: the period of accelerated fall and the period of constant-velocity fall. The initial acceleration period is usually very short, on the order of a tenth of a second or so. Hence, the period of constant-velocity fall is the important one. The velocity is called the free settling velocity or terminal velocity ν_t.

To solve for the terminal velocity in Eq. (14.3-5), dν/dt = 0 and the equation becomes

Equation 14.3-6

For spherical particles and . Substituting these into Eq. (14.3-6), we obtain, for spherical particles,

Equation 14.3-7

where ν_t is m/s (ft/s), ρ is kg/m³ (lb_m/ft³), g is 9.80665 m/s² (32.174 ft/s²), and D_p is m (ft).

2. Drag coefficient for rigid spheres

The drag coefficient for rigid spheres has been shown to be a function of the Reynolds number D_pνρ/μ of the sphere and is shown in Fig. 14.3-1. In the laminar-ow region, called the Stokes' law region for N_Re < 1, as discussed in Section 3.1B, the drag coefficient is

Equation 14.3-8

where μ is the viscosity of the liquid in Pa · s or kg/m · s (lb_m/ft s). Substituting this into Eq. (14.3-7) for laminar flow,

Equation 14.3-9

For other shapes of particles, drag coefficients will differ from those given in Fig. 14.3-1, and data are given in Fig. 3.1-2 and elsewhere (B2, L2, P1). In the turbulent Newton's law region above a Reynolds number of about 1000 to 2.0 × 10⁵, the drag coefficient is approximately constant at C_D = 0.44.

Solution of Eq. (14.3-7) is by trial and error when the particle diameter is known and the terminal velocity is to be obtained, because C_D also depends upon the velocity ν_t.

If the particles are quite small, Brownian motion is present. Brownian motion is the random motion imparted to the particle by collisions between the molecules of the fluid surrounding the particle and the particle. This movement of the particles in random directions tends to suppress the effect of gravity, so settling of the particles may occur more slowly or not at all. At particle sizes of a few micrometers, the Brownian effect becomes appreciable, and at sizes of less than 0.1 μm, the effect predominates. For very small particles, application of centrifugal force helps reduce the effect of Brownian motion.

EXAMPLE 14.3-1. Settling Velocity of Oil Droplets Oil droplets having a diameter of 20 μm (0.020 mm) are to be settled from air at temperature of 37.8°C (311 K) and 101.3 kPa pressure. The density of the oil is 900 kg/m3. Calculate the terminal settling velocity of the droplets. Solution: The various knowns are Dp = 2.0 × 10−5 m and ρp = 900 kg/m3. From Appendix A.3, for air at 37.8°C, ρ = 1.137 kg/m3, μ = 1.90 × 10−5 Pa · s. The droplet will be assumed to be a rigid sphere. The solution is trial and error since the velocity is unknown. Hence, CD cannot be directly determined. The Reynolds number is as follows: Equation 14.3-10 For the first trial, assume that νt = 0.305 m/s. Then NRe = 1.197(0.305) = 0.365. Substituting into Eq. (14.3-7) and solving for CD, Equation 14.3-11 Using νt = 0.305 m/s, CD = 0.2067/(0.305)2 = 2.22. Assuming that νt = 0.0305 m/s, NRe = 0.0365 from Eq. (14.3-10) and CD = 222 from Eq. (14.3-11). For the third trial, assuming that νt = 0.00305 m/s, NRe = 0.00365 and CD = 22 200. These three values calculated for NRe and CD are plotted on a graph similar to Fig. 14.3-1 and shown in Fig. 14.3-2. It can be shown that the line through these points is a straight line. The intersection of this line and the drag-coefficient correlation line is the solution to the problem at NRe = 0.012. The velocity can be calculated from the Reynolds number in Eq. (14.3-10): Figure 14.3-2. Solution of Example 14.3-1 for settling velocity of a particle. The particle is in the Reynolds number range less than 1, which is the laminar Stokes' law region. Alternatively, the velocity can be calculated by substituting into Eq. (14.3-9): Note that Eq. (14.3-9) could not be used until it was determined that the particle fall was in the laminar region.

For particles that are rigid but nonspherical, the drag depends upon the shape of the particle and the orientation of the particle with respect to its motion. Correlations of drag coefficients for particles of different shapes are given in a number of references (B2, C1, P1).

3. Drag coefficients for nonrigid spheres

When particles are nonrigid, internal circulation inside the particle and particle deformation can occur. Both of these effects affect the drag coefficient and terminal velocity. Drag coefficients for air bubbles rising in water are given in Perry and Green (P1), and for a Reynolds number less than about 50, the curve is the same as for rigid spheres in water.

For liquid drops in gases, the same drag relationship as for solid spherical particles is obtained up to a Reynolds number of about 100 (H1). Large drops will deform with an increase in drag. Small liquid drops in immiscible liquids behave like rigid spheres and the drag coefficient curve follows that for rigid spheres up to a Reynolds number of about 10. Above this and up to a Reynolds number of 500, the terminal velocity is greater than that for solids because of internal circulation in the drop.

14.3C. Hindered Settling

For many cases of settling, a large number of particles are present, and the surrounding particles interfere with the motion of individual particles. The velocity gradients surrounding each particle are affected by the close presence of other particles. The particles settling in the liquid displace the liquid, and an appreciable upward velocity of the liquid is generated. Hence, the velocity of the liquid is appreciably greater with respect to the particle than with respect to the apparatus itself.

For such hindered flow, the settling velocity is less than would be calculated from Eq. (14.3-9) for Stokes' law. The true drag force is greater in the suspension because of the interference of the other particles. This higher effective viscosity of the mixture μ_m is equal to the actual viscosity of the liquid itself, μ, divided by an empirical correction factor, , which depends upon ε, the volume fraction of the slurry mixture occupied by the liquid (S1):

Equation 14.3-12

where is dimensionless and is as follows (S1):

Equation 14.3-13

The density of the fluid phase effectively becomes the bulk density of the slurry ρ_m, which is as follows:

Equation 14.3-14

where ρ_m is density of slurry in kg solid + liquid/m³. The density difference is now

Equation 14.3-15

The settling velocity, ν_t with respect to the apparatus is ε times the velocity calculated by Stokes' law.

Substituting mixture properties of μ_m from Eq. (14.3-12) for μ in Eq. (14.3-9), (ρ_p − ρ_m) from Eq. (14.3-15) for (ρ_p − ρ), and multiplying the result by ε for the relative-velocity effect, Eq. (14.3-9) becomes, for laminar settling,

Equation 14.3-16

This is the velocity calculated from Eq. (14.3-9), multiplied by the correction factor ().

The Reynolds number is then based on the velocity relative to the fluid and is

Equation 14.3-17

When the Reynolds number is less than 1, the settling is in the Stokes' law range. For Reynolds numbers above 1.0, see (P1). The effect of concentration is greater for nonspherical particles and angular particles (S1).

EXAMPLE 14.3-2. Hindered Settling of Glass Spheres Calculate the settling velocity of glass spheres having a diameter of 1.554 × 10−4 m (5.10 × 10−4 ft) in water at 293.2 K (20°C). The slurry contains 60 wt % solids. The density of the glass spheres is ρp = 2467 kg/m3 (154 lbm/ft3). Solution: Density of water ρ = 998 kg/m3 (62.3 lbm/ft3), and viscosity of water μ = 1.005 × 10−3 Pa · s (6.72 × 10−4 lbm/ft · s). To calculate the volume fraction ε of the liquid, The bulk density of the slurry ρm according to Eq. (14.3-14) is Substituting into Eq. (14.3-13), Substituting into Eq. (14.3-16), using SI and English units, The Reynolds number is obtained by substituting into Eq. (14.3-17): Hence, the settling is in the laminar range.

14.3D. Wall Effect on Free Settling

When the diameter D_p of the particle becomes appreciable with respect to the diameter D_W of the container in which the settling is occurring, a retarding effect known as the wall effect is exerted on the particle. The terminal settling velocity is reduced. In the case of settling in the Stokes' law regime, the computed terminal velocity can be multiplied by the following to allow for the wall effect (Z1) for D_p/D_W < 0.05:

Equation 14.3-18

For a completely turbulent regime, the correction factor is

Equation 14.3-19

14.3E. Differential Settling and Separation of Solids in Classification

1. Sink-and-float methods

Devices for the separation of solid particles into several fractions based upon their rates of flow or settling through fluids are known as classifiers. There are several separation methods for accomplishing this, namely, sink-and-float and differential settling. In the sink-and-float method, a liquid is used whose density is intermediate between that of the heavy or high-density material and that of the light-density material. In this liquid, the heavy particles will not float but settle out from the medium, while the light particles will float.

This method is independent of the sizes of the particles and depends only upon the relative densities of the two materials. This means liquids used must have densities greater than water, since most solids have high densities. Unfortunately, few such liquids exist that are cheap and noncorrosive. As a result, pseudoliquids are used, consisting of a suspension in water of very fine solid materials with high specific gravities, such as galena (specific gravity = 7.5) and magnetite (specific gravity = 5.17).

Hindered settling is used and the bulk density of the medium can be varied widely by varying the amount of the fine solid materials in the medium. Common applications of this technique are concentrating ore materials and cleaning coal. The fine solid materials in the medium are so small in diameter that their settling velocity is negligible, giving a relatively stable suspension.

2. Differential settling methods

The separation of solid particles into several size fractions based upon their settling velocities in a particular medium is called differential settling or classification. The density of the medium is less than that of either of the two substances to be separated.

In differential settling, both light and heavy materials settle through the medium. A disadvantage of this method if the light and heavy materials both have a range of particle sizes is that the smaller heavy particles settle at the same terminal velocity as the larger light particles.

Suppose that we consider two different materials: heavy-density material A (such as galena, with a specific gravity ρ_A = 7.5) and light-density material B (such as quartz, with a specific gravity ρ_B = 2.65). The terminal settling velocity of components A and B, from Eq. (14.3-7), can be written

Equation 14.3-20

Equation 14.3-21

For particles of equal settling velocities, ν_tA = ν_tB and we obtain, by equating Eq. (14.3-20) to (14.3-21), canceling terms, and squaring both sides,

Equation 14.3-22

or

Equation 14.3-23

For particles that are essentially spheres at very high Reynolds numbers in the turbulent Newton's law region, C_D is constant and C_DA = C_DB, giving

Equation 14.3-24

For laminar Stokes' law settling,

Equation 14.3-25

Substituting Eq. (14.3-25) into (14.3-23) and rearranging for Stokes' law settling, where ν_tA = ν_tB,

Equation 14.3-26

For transition flow between laminar and turbulent flow,

Equation 14.3-27

For particles settling in the turbulent range, Eq. (14.3-24) holds for equal settling velocities. For particles where D_pA = D_pB and settling is in the turbulent Newton's law region, combining Eqs. (14.3-20) and (14.3-21),

Equation 14.3-28

If both A and B particles are settling in the same medium, then Eqs. (14.3-24) and (14.3-28) can be used to make the plots given in Fig. 14.3-3 for the relation of velocity to diameter for A and B.

First, we consider a mixture of particles of materials A and B with a size range of D_p1 to D_p4 for both types of material. In the size range D_p1 to D_p2 in Fig. 14.3-3, a pure fraction of substance B can be obtained, since no particles of A settle as slowly. In the size range D_p3 to D_p4, a pure fraction of A can be obtained, since no B particles settle as fast as the A particles in this size range. In the size range D_p1 to D_p3, A particles settle as rapidly as B particles in the size range D_p2 to D_p4, forming a mixed fraction of A and B.

Increasing the density ρ of the medium in Eq. (14.3-24), the numerator becomes smaller proportionately faster than the denominator, and the spread between D_pA and D_pB is increased. Somewhat similar curves are obtained in the Stokes' law region.

EXAMPLE 14.3-3. Separation of a Mixture of Silica and Galena A mixture of silica (B) and galena (A) solid particles having a size range of 5.21 × 10−6 m to 2.50 × 10−5 m is to be separated by hydraulic classification using free settling conditions in water at 293.2 K (B1). The specific gravity of silica is 2.65 and that of galena is 7.5. Calculate the size range of the various fractions obtained in the settling. If the settling is in the laminar region, the drag coefficients will be reasonably close to that for spheres. Solution: The particle-size range is Dp = 5.21 × 10−6 m to Dp = 2.50 × 10−5 m. Densities are ρpA = 7.5(1000) = 7500 kg/m3, ρpB = 2.65(1000) = 2650 kg/m3, ρ = 998 kg/m3 for water at 293.2 K (20°C). The water viscosity μ = 1.005 × 10−3 Pa · s = 1.005 × 10−3 kg/ms. Assuming Stokes' law settling, Eq. (14.3-9) becomes as follows: Equation 14.3-29 The largest Reynolds number occurs for the largest particle and the biggest density, where DpA = 2.50 × 10−5 m and ρpA = 7500. Substituting into Eq. (14.3-29), Substituting into the Reynolds number equation, Equation 14.3-30 Hence, the settling is in the Stokes' law region. Referring to Fig. 14.3-3 and using the same nomenclature, the largest size is Dp4 = 2.50 × 10−5 m. The smallest size is Dp1 = 5.21 × 10−6 m. The pure fraction of A consists of DpA4 = 2.50 × 10−5 m to DpA3. The particles, having diameters DpA3 and DpB4, are related by having equal settling velocities in Eq. (14.3-26). Substituting DpB4 = 2.50 × 10−5 m into Eq. (14.3-26) and solving, The size range of pure B fraction is DpB2 to DpB1 = 5.21 × 10−6 m. The diameter DpB2 is related to DpA1 = 5.21 × 10−6 by Eq. (14.3-26) at equal settling velocities: The three fractions recovered are as follows: The size range of the first fraction of pure A (galena) is as follows: The mixed-fraction size range is as follows: The size range of the third fraction of pure B (silica) is as follows:

14.3F. Sedimentation and Thickening

1. Mechanisms of sedimentation

When a dilute slurry is settled by gravity into a clear fluid and a slurry of higher solids concentration, the process is called sedimentation or sometimes thickening. To illustrate the method for determining settling velocities and the mechanisms of settling, a batch settling test is carried out by placing a uniform concentration of the slurry in a graduated cylinder. At the start, as shown in Fig. 14.3-4a, all the particles settle by free settling in suspension zone B. The particles in zone B settle at a uniform rate at the start, and a clear liquid zone A appears in Fig. 14.3-4b. The height z drops at a constant rate. Also, zone D begins to appear, which contains the settled particles at the bottom. Zone C is a transition layer whose solids content varies from that in zone B to that in zone D. After further settling, zones B and C disappear, as shown in Fig. 14.3-4c. Then compression first appears; this moment is called the critical point. During compression, liquid is expelled upward from zone D and the thickness of zone D decreases.

2. Determination of settling velocity

In Fig. 14.3-4d the height z of the clear-liquid interface is plotted versus time. As shown, the velocity of settling, which is the slope of the line, is constant at first. The critical point is shown at point C. Since sludges vary greatly in their settling rates, experimental rates for each sludge are necessary. Kynch (K1) and Talmage and Fitch (T1) describe a method for predicting thickener sizes from the batch settling test.

The settling velocity ν is determined by drawing a tangent to the curve in Fig. 14.3-4d at a given time t₁, with slope −dz/dt = ν₁. At this point the height is z₁, and z_i is the intercept of the tangent to the curve. Then,

Equation 14.3-31

The concentration c₁ is, therefore, the average concentration of the suspension if z_i is the height of this slurry. This is calculated by

Equation 14.3-32

where c₀ is the original slurry concentration in kg/m³ at z₀ height and t = 0. This is repeated for other times, and a plot of settling velocity versus concentration is made. Further details of this and other methods of designing the thickener are given elsewhere (C1, F1, F2, T1, P1). These and other methods in the literature are highly empirical and care should be exercised in their use.

14.3G. Equipment for Settling and Sedimentation

1. Simple gravity settling tank

In Fig. 14.3-5a a simple gravity settler is shown for removing by settling a dispersed liquid phase from another phase. The velocity horizontally to the right must be slow enough to allow time for the smallest droplets to rise from the bottom to the interface or from the top down to the interface and coalesce.

In Fig. 14.3-5b a gravity settling chamber is shown schematically. Dust-laden air enters at one end of a large, boxlike chamber. Particles settle toward the floor at their terminal settling velocities. The air must remain in the chamber a sufficient length of time (residence time) so that the particles reach the floor of the chamber. Knowing the throughput of the air stream through the chamber and the chamber size, the residence time of the air in the chamber can be calculated. The vertical height of the chamber must be small enough that this height, divided by the settling velocity, gives a time less than the residence time of the air.

2. Equipment for classification

The simplest type of classifier is one in which a large tank is subdivided into several sections, as shown in Fig. 14.3-6. A liquid slurry feed enters the tank containing a size range of solid particles. The larger, faster-settling particles settle to the bottom close to the entrance and the slower-settling particles settle to the bottom close to the exit. The linear velocity of the entering feed decreases as a result of the enlargement of the cross-sectional area at the entrance. The vertical baffles in the tank allow for the collection of several fractions. The settling-velocity equations derived in this section hold.

3. Spitzkasten classifier

Another type of gravity settling chamber is the Spitzkasten, shown in Fig. 14.3-7, which consists of a series of conical vessels of increasing diameter in the direction of flow. The slurry enters the first vessel, where the largest and fastest-settling particles are separated. The overflow goes to the next vessel, where another separation occurs. This continues in the succeeding vessel or vessels. In each vessel the velocity of upflowing inlet water is controlled to give the desired size range for each vessel.

4. Sedimentation thickener

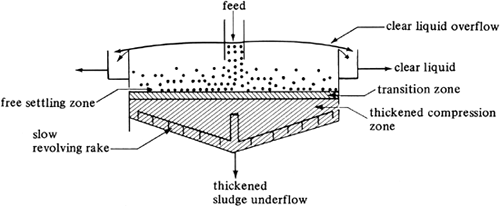
The separation of a dilute slurry by gravity settling into a clear fluid and a slurry of higher solids concentration is called sedimentation. Industrially, sedimentation operations are often carried out continuously in equipment called thickeners. A continuous thickener with a slowly revolving rake for removing the sludge or thickened slurry is shown in Fig. 14.3-8.

The slurry in Fig. 14.3-8 is fed at the center of the tank several feet below the surface of the liquid. Around the top edge of the tank is a clear-liquid-overflow outlet. The rake serves to scrape the sludge toward the center of the bottom for removal. This gentle stirring aids in removing water from the sludge.

In the thickener the entering slurry spreads radially through the cross section of the thickener and the liquid flows upward and out the overflow. The solids settle in the upper zone by free settling. Below this dilute settling zone is the transition zone, in which the concentration of solids increases rapidly, and then the compression zone. A clear overflow can be obtained if the upward velocity of the fluid in the dilute zone is less than the minimal terminal settling velocity of the solids in this zone.

The settling rates are quite slow in the thickened zone, which consists of a compression of the solids with liquid being forced upward through the solids. This is an extreme case of hindered settling. Equation (14.3-16) may be used to estimate the settling velocities, but the results can be in considerable error because of agglomeration of particles. As a result, laboratory settling or sedimentation data must be used in the design of a thickener, as discussed previously in Section 14.3F.