3.6. DIFFERENTIAL EQUATIONS OF CONTINUITY

3.6A. Introduction

In Sections 2.6, 2.7, and 2.8, overall mass, energy, and momentum balances allowed us to solve many elementary problems in fluid flow. These balances were done on an arbitrary finite volume sometimes called a control volume. In these total-energy, mechanical-energy, and momentum balances, we only needed to know the state of the inlet and outlet streams and the exchanges with the surroundings.

These overall balances were powerful tools in solving various flow problems because they did not require knowledge of what goes on inside the finite control volume. Also, in the simple shell-momentum balances made in Section 2.9, expressions were obtained for the velocity distribution and pressure drop. However, to advance in our study of these flow systems, we must investigate in greater detail what goes on inside this finite control volume. To do this, we now use a differential element for a control volume. The differential balances will be somewhat similar to the overall and shell balances, but now we shall make the balance in a single phase and integrate to the phase boundary using the boundary conditions. In the balances done earlier, a balance was made for each new system studied. It is not necessary to formulate new balances for each new flow problem. It is often easier to start with the differential equations for the conservation of mass (equation of continuity) and the conservation of momentum in general form. Then these equations are simplified by discarding unneeded terms for each particular problem.

For nonisothermal systems, a general differential equation for conservation of energy will be considered in Chapter 5. Also, in Chapter 7, a general differential equation of continuity for a binary mixture will be derived. The differential-momentum-balance equation to be derived is based on Newton's second law and allows us to determine the way velocity varies with position and time as well as the pressure drop in laminar flow. The equation of momentum balance can be used for turbulent flow with certain modifications.

Often these conservation equations are called equations of change, since they describe the variations in the properties of the fluid with respect to position and time. Before we derive these equations, a brief review of the different types of derivatives with respect to time which occur in these equations and a brief description of vector notation will be given.

3.6B. Types of Time Derivatives and Vector Notation

1. Partial time derivative

Various types of time derivatives are used in the derivations to follow. The most common type of derivative is the partial time derivative. For example, suppose that we are interested in the mass concentration or density ρ in kg/m³ in a flowing stream as a function of position x, y, z and time t. The partial time derivative of ρ is ∂ρ/∂t. This is the local change of density with time at a fixed point x, y, z.

2. Total time derivative

Suppose that we want to measure the density in the stream while we are moving about in the stream with velocities in the x, y, and z directions of dx/dt, dy/dt, and dz/dt, respectively. The total derivative dρ/dt is

Equation 3.6-1

This means that the density is a function of t and of the velocity components dx/dt, dy/dt, and dz/dt at which the observer is moving.

3. Substantial time derivative

Another useful type of time derivative is obtained if the observer floats along with the velocity ν of the flowing stream and notes the change in density with respect to time. This is called the derivative that follows the motion, or the substantial time derivative, Dρ/Dt:

Equation 3.6-2

where ν_x, ν_y, and ν_z are the velocity components of the stream velocity ν, which is a vector. This substantial derivative is applied to both scalar and vector variables. The term (ν · ∇ρ) will be discussed in part 6 of Section 3.6B.

4. Scalars

The physical properties encountered in momentum, heat, and mass transfer can be placed in several categories: scalars, vectors, and tensors. Scalars are quantities such as concentration, temperature, length, volume, time, and energy. They have magnitude but no direction and are considered to be zero-order tensors. The common mathematical algebraic laws hold for the algebra of scalars. For example, bc = cd, b(cd) = (bc)d, and so on.

5. Vectors

Velocity, force, momentum, and acceleration are considered vectors since they have magnitude and direction. They are regarded as first-order tensors and are written in boldface letters in this text, such as ν for velocity. The addition of two vectors B + C by parallelogram construction and the subtraction of two vectors B - C are shown in Fig. 3.6-1. The vector B is represented by its three projections B_x, B_y, and B_z on the x, y, and z axes, and

Equation 3.6-3

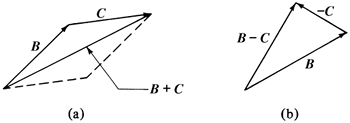
where i, j, and k are unit vectors along the axes x, y, and z, respectively.

In multiplying a scalar quantity r or s by a vector B, the following hold:

Equation 3.6-4

Equation 3.6-5

Equation 3.6-6

The following also hold:

Equation 3.6-7

Equation 3.6-8

Equation 3.6-9

Equation 3.6-10

where ϕ_BC is the angle between two vectors and is <180°.

Second-order tensors τ arise primarily in momentum transfer and have nine components. They are discussed elsewhere (B2).

6. Differential operations with scalars and vectors

The gradient or "grad" of a scalar field is

Equation 3.6-11

where ρ is a scalar such as density.

The divergence or "div" of a vector ν is

Equation 3.6-12

where ν is a function of ν_x, ν_y, and ν_z.

The Laplacian of a scalar field is

Equation 3.6-13

Other operations that may be useful are

Equation 3.6-14

Equation 3.6-15

Equation 3.6-16

3.6C. Differential Equation of Continuity

1. Derivation of equation of continuity

A mass balance will be made for a pure fluid flowing through a stationary volume element Δx Δy Δz which is fixed in space as in Fig. 3.6-2. The mass balance for the fluid with a concentration of ρ kg/m³ is

Equation 3.6-17

In the x direction the rate of mass entering the face at x having an area of Δy Δz m² is (ρv_x)_x Δy Δz kg/s and that leaving at x + Δx is (ρν_x)_x+Δx Δy Δz. The term (ρν_x) is a mass flux in kg/s · m². Mass entering and mass leaving in the y and z directions are also shown in Fig. 3.6-2.

The rate of mass accumulation in the volume Δx Δy Δz is

Equation 3.6-18

Substituting all these expressions into Eq. (3.6-17) and dividing both sides by Δx Δy Δz,

Equation 3.6-19

Taking the limit as Δx, Δy, and Δz approach zero, we obtain the equation of continuity or conservation of mass for a pure fluid:

Equation 3.6-20

The vector notation on the right side of Eq. (3.6-20) comes from the fact that ν is a vector. Equation (3.6-20) tells us how density ρ changes with time at a fixed point resulting from the changes in the mass velocity vector ρν.

We can convert Eq. (3.6-20) into another form by carrying out the actual partial differentiation:

Equation 3.6-21

Rearranging Eq. (3.6-21),

Equation 3.6-22

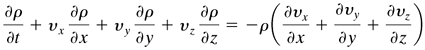
The left-hand side of Eq. (3.6-22) is the same as the substantial derivative in Eq. (3.6-2). Hence, Eq. (3.6-22) becomes

Equation 3.6-23

2. Equation of continuity for constant density

Often in engineering with liquids that are relatively incompressible, the density ρ is essentially constant. Then ρ remains constant for a fluid element as it moves along a path following the fluid motion, or Dρ/Dt = 0. Hence, Eq. (3.6-23) becomes, for a fluid of constant density at steady or unsteady state,

Equation 3.6-24

At steady state, ∂p/∂t = 0 in Eq. (3.6-22).

EXAMPLE 3.6-1. Flow over a Flat Plate An incompressible fluid flows past one side of a flat plate. The flow in the x direction is parallel to the flat plate. At the leading edge of the plate the flow is uniform at the free stream velocity νx0. There is no velocity in the z direction. The y direction is the perpendicular distance from the plate. Analyze this case using the equation of continuity. Solution: For this case where ρ is constant, Eq. (3.6-24) holds: Equation 3.6-24 Since there is no velocity in the z direction, we obtain Equation 3.6-25 At a given small value of y close to the plate, the value of νx must decrease from its free stream velocity vx0 as it passes the leading edge in the x direction because of fluid friction. Hence, ∂νx/∂x is negative. Then from Eq. (3.6-25), ∂νy/∂y is positive and there is a component of velocity away from the plate.

3. Continuity equation in cylindrical and spherical coordinates

It is often convenient to use cylindrical coordinates to solve the equation of continuity if fluid is flowing in a cylinder. The coordinate system as related to rectangular coordinates is shown in Fig. 3.6-3a. The relations between rectangular x, y, z and cylindrical r, θ, z coordinates are

Equation 3.6-26

Using the relations from Eq. (3.6-26) with Eq. (3.6-20), the equation of continuity in cylindrical coordinates is

Equation 3.6-27

For spherical coordinates the variables r, θ, and ϕ are related to x, y, z by the following, as shown in Fig. 3.6-3b:

Equation 3.6-28

The equation of continuity in spherical coordinates becomes

Equation 3.6-29