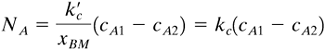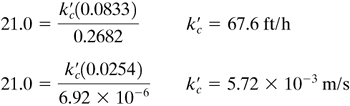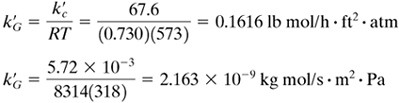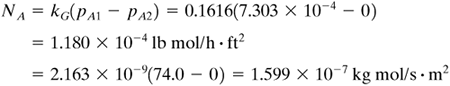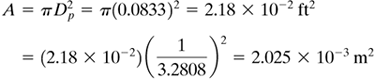7.3. MASS-TRANSFER COEFFICIENTS FOR VARIOUS GEOMETRIES

7.3A. Dimensionless Numbers Used to Correlate Data

The experimental data for mass-transfer coefficients obtained using various kinds of fluids, different velocities, and different geometries are correlated using dimensionless numbers similar to those for heat and momentum transfer. Methods of dimensional analysis are discussed in Sections 3.11, 4.14, and 7.8.

The most important dimensionless number is the Reynolds number N_Re, which indicates degree of turbulence:

Equation 7.3-1

where L is diameter D_p for a sphere, diameter D for a pipe, or length L for a flat plate. The velocity ν is the mass average velocity if in a pipe. In a packed bed the superficial velocity ν' in the empty cross section is often used, or sometimes ν = ν'/ε is used, where ν is interstitial velocity and є void fraction of bed.

The Schmidt number is

Equation 7.3-2

The viscosity μ and density ρ used are for the actual flowing mixture of solute A and fluid B. If the mixture is dilute, properties of the pure fluid B can be used. The Prandtl number c_pμ/k for heat transfer is analogous to the Schmidt number for mass transfer. The Schmidt number is the ratio of the shear component for diffusivity μ/ρ to the diffusivity for mass transfer D_AB; it physically relates the relative thickness of the hydrodynamic layer and mass-transfer boundary layer.

The Sherwood number, which is dimensionless, is

Equation 7.3-3

Other substitutions from Table 7.2-1 can be made for in Eq. (7.3-3).

The Stanton number occurs often and is

Equation 7.3-4

Again, substitution for can be made. G_M = νρ/M_av = νc.

Often the mass-transfer coefficient is correlated as a dimensionless J_D factor, which is related to and N_Sh as follows:

Equation 7.3-5

For heat transfer a dimensionless J_H factor is as follows:

Equation 7.3-6

7.3B. Analogies Among Mass, Heat, and Momentum Transfer

1. Introduction

In molecular transport of momentum, heat, or mass there are many similarities, which were pointed out in Chapters 2–6. The molecular diffusion equations of Newton for momentum, Fourier for heat, and Fick for mass are very similar, and we can say that we have analogies among these three molecular transport processes. There are also similarities in turbulent transport, as discussed in Sections 5.7C and 6.1A, where the flux equations were written using the turbulent eddy momentum diffusivity ε_t, the turbulent eddy thermal diffusivity α_t, and the turbulent eddy mass diffusivity ε_M. However, these similarities are not as well defined mathematically or physically and are more difficult to relate to each other.

A great deal of effort has been devoted in the literature to developing analogies among these three transport processes for turbulent transfer so as to allow prediction of one from any of the others. We discuss several next.

2. Reynolds analogy

Reynolds was the first to note similarities in transport processes and relate turbulent momentum and heat transfer. Since then, mass transfer has also been related to momentum and heat transfer. We derive this analogy from Eqs. (6.1-4)–(6.1-6) for turbulent transport. For fluid flow in a pipe, for heat transfer from the fluid to the wall, Eq. (6.1-5) becomes as follows, where z is distance from the wall:

Equation 7.3-7

For momentum transfer, Eq. (6.1-4) becomes

Equation 7.3-8

Next we assume that α and μ/ρ are negligible and that α_t = ε_t. Then dividing Eq. (7.3-7) by (7.3-8),

Equation 7.3-9

If we assume that heat flux q/A in a turbulent system is analogous to momentum flux τ, the ratio τ/(q/A) must be constant for all radial positions. We now integrate between conditions at the wall where T = T_i and ν = 0 to some point in the fluid where T is the same as the bulk T, and assume that the velocity at this point is the same as ν_av, the bulk velocity. Also, q/A is understood to be the flux at the wall, as is the shear at the wall, written as τ_s. Hence,

Equation 7.3-10

Also, substituting q/A = h(T − T_i) and from Eq. (2.10-4) into Eq. (7.3-10),

Equation 7.3-11

In a similar manner, using Eq. (6.1-6) for and , we can relate this to Eq. (7.3-8) for momentum transfer. Then, the complete Reynolds analogy is

Equation 7.3-12

Experimental data for gas streams agree approximately with Eq. (7.3-12) if the Schmidt and Prandtl numbers are near 1.0 and only skin friction is present in flow past a flat plate or inside a pipe. When liquids are present and/or form drag is present, the analogy is not valid.

3. Other analogies

The Reynolds analogy assumes that the turbulent diffusivities ε_t, α_t, and ε_M are all equal and that the molecular diffusivities μ/ρ, α, and D_AB are negligible compared to the turbulent diffusivities. When the Prandtl number (μ/ρ)/α is 1.0, then μ/ρ = α; also, for N_Sc = 1.0, μ/ρ = D_AB. Then, (μ/ρ + ε_t) = (α + α_t) = (D_AB + ε_M) and the Reynolds analogy can be obtained with the molecular terms present. However, the analogy breaks down when the viscous sublayer becomes important, since the eddy diffusivities diminish to zero and the molecular diffusivities become important.

Prandtl modified the Reynolds analogy by writing the regular molecular diffusion equation for the viscous sublayer and a Reynolds analogy equation for the turbulent core region. Then, since these processes are in series, these equations were combined to produce an overall equation (G1). The results again are poor for fluids where the Prandtl and Schmidt numbers differ from 1.0.

Von Kármán further modified the Prandtl analogy by considering the buffer region in addition to the viscous sublayer and the turbulent core. These three regions are shown in the universal velocity profile in Fig. 3.10-4. Again, an equation is written for molecular diffusion in the viscous sublayer using only the molecular diffusivity and a Reynolds analogy equation for the turbulent core. Both the molecular and eddy diffusivity are used in an equation for the buffer layer, where the velocity in this layer is used to obtain an equation for the eddy diffusivity. These three equations are then combined to give the von Kármán analogy. Since then, numerous other analogies have appeared (P1, S4).

4. Chilton and Colburn J-factor analogy

The most successful and most widely used analogy is the Chilton and Colburn J-factor analogy (C2). This analogy is based on experimental data for gases and liquids in both the laminar and turbulent flow regions and is written as follows:

Equation 7.3-13

Although this is an equation based on experimental data for both laminar and turbulent flow, it can be shown to satisfy the exact solution derived from laminar flow over a flat plate in Sections 3.10 and 5.7.

Equation (7.3-13) has been shown to be quite useful in correlating momentum, heat, and mass-transfer data. It permits the prediction of an unknown transfer coefficient when one of the other coefficients is known. In momentum transfer the friction factor is obtained for the total drag or friction loss, which includes form drag or momentum losses due to blunt objects as well as skin friction. For flow past a flat plate or in a pipe, where no form drag is present, f/2 = J_H = J_D. When form drag is present, as in flow in packed beds or past other blunt objects, f/2 is greater than J_H or J_D, and J_H ≅ J_D.

7.3C. Derivation of Mass-Transfer Coefficients in Laminar Flow

1. Introduction

When a fluid is flowing in laminar flow and mass transfer by molecular diffusion is occurring, the equations are very similar to those for heat transfer by conduction in laminar flow. The phenomena of heat and mass transfer are not always completely analogous, since in mass transfer several components may be diffusing. Also, the flux of mass perpendicular to the direction of the flow must be small so as not to distort the laminar velocity profile.

In theory it is not necessary to have experimental mass-transfer coefficients for laminar flow, since the equations for momentum transfer and diffusion can be solved. However, in many actual cases it is difficult to describe mathematically the laminar flow for certain geometries, such as flow past a cylinder or in a packed bed. Hence, experimental mass-transfer coefficients are often obtained and correlated. A simplified theoretical derivation will be given for two cases of laminar flow.

2. Mass transfer in laminar flow in a tube

We consider the case of mass transfer from a tube wall to a fluid inside in laminar flow, where, for example, the wall is made of solid benzoic acid which is dissolving in water. This is similar to heat transfer from a wall to the flowing fluid where natural convection is negligible. For fully developed flow, the parabolic velocity derived as Eqs. (2.6-18) and (2.6-20) is

Equation 7.3-14

where ν_x is the velocity in the x direction at the distance r from the center. For steady state diffusion in a cylinder, a mass balance can be made on a differential element where the rate in by convection plus diffusion equals the rate out radially by diffusion to give

Equation 7.3-15

Then, ∂²c_A/∂x² = 0 if the diffusion in the x direction is negligible compared to that by convection. Combining Eqs. (7.3-14) and (7.3-15), the final solution (S1) is a complex series similar to the Graetz solution for heat transfer and a parabolic velocity profile.

If it is assumed that the velocity profile is flat, as in rodlike flow, the solution is more easily obtained (S1). A third solution, called the approximate Leveque solution, has been obtained, where there is a linear velocity profile near the wall and the solute diffuses only a short distance from the wall into the fluid. This is similar to the parabolic-velocity-profile solution at high flow rates. Experimental design equations are presented in Section 7.3D for this case.

3. Diffusion in a laminar falling film

In Section 2.9C we derived the equation for the velocity profile in a falling film shown in Fig. 7.3-1a. We will consider mass transfer of solute A into a laminar falling film, which is important in wetted-wall columns, in developing theories to explain mass transfer in stagnant pockets of fluids, and in turbulent mass transfer. The solute A in the gas is absorbed at the interface and then diffuses a distance into the liquid so that it has not penetrated the whole distance × = δ at the wall. At steady state the inlet concentration c_A = 0. The concentration profile of c_A at a point z distance from the inlet is shown in Fig. 7.3-1a.

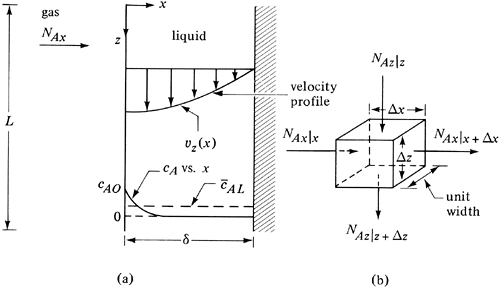
A mass balance will be made on the element shown in Fig. 7.3-1b. For steady state, rate of input = rate of output:

Equation 7.3-16

For a dilute solution the diffusion equation for A in the x direction is

Equation 7.3-17

For the z direction the diffusion is negligible:

Equation 7.3-18

Dividing Eq. (7.3-16) by Δx Δz, letting Δx and Δz approach zero, and substituting Eqs. (7.3-17) and (7.3-18) into the result, we obtain

Equation 7.3-19

From Eqs. (2.9-24) and (2.9-25), the velocity profile is parabolic and is ν_z = ν_zmax [1 − (×/δ²)]. Also, . If the solute has penetrated only a short distance into the fluid, that is, short contact times of t = z/ν_max, then the A that has diffused has been carried along at the velocity ν_zmax, or ν_max if the subscript z is dropped. Then Eq. (7.3-19) becomes

Equation 7.3-20

Using the boundary conditions of c_A = 0 at z = 0, c_A = c_A0 at × = 0, and c_A = 0 at × = ∞, we can integrate Eq. (7.3-20) to obtain

Equation 7.3-21

where erf y is the error function and erfc y = 1 − erf y. Values of erf y are standard tabulated functions.

To determine the local molar flux at the surface × = 0 at position z from the top entrance, we write (B1)

Equation 7.3-22

The total moles of A transferred per second to the liquid over the entire length z = 0 to z = L, where the vertical surface is unit width, is

Equation 7.3-23

The term L/ν_max is t_L, time of exposure of the liquid to the solute A in the gas. This means the rate of mass transfer is proportional to and . This is the basis for the penetration theory in turbulent mass transfer where pockets of liquid are exposed to unsteady-state diffusion (penetration) for short contact times.

7.3D. Mass Transfer for Flow Inside Pipes

1. Mass transfer for laminar flow inside pipes

When a liquid or gas is flowing inside a pipe and the Reynolds number Dνρ/μ is below 2100, laminar flow occurs. Experimental data obtained for mass transfer from the walls for gases (G2, L1) are plotted in Fig. 7.3-2 for values of W/D_ABρL less than about 70. The ordinate is (c_A − c_A0)/(c_Ai − c_A0), where c_A is the exit concentration, c_A0 inlet concentration, and c_Ai concentration at the interface between the wall and the gas. The dimensionless abscissa is W/D_ABρL or N_ReN_Sc(D/L)(π/4), where W is flow in kg/s and L is length of mass-transfer section in m. Since the experimental data follow the rodlike plot, that line should be used. The velocity profile is assumed fully developed to parabolic form at the entrance.

For liquids that have small values of D_AB, data follow the parabolic flow line, which is as follows for W/D_ABρL over 400:

Equation 7.3-24

2. Mass transfer for turbulent flow inside pipes

For turbulent flow when Dνρ/μ > 2100 for gases or liquids flowing inside a pipe,

Equation 7.3-25

The equation holds for N_Sc of 0.6 to 3000 (G2, L1). Note that the N_Sc for gases is in the range 0.5–3 and for liquids is above 100 in general. Equation (7.3-25) for mass transfer and Eq. (4.5-8) for heat transfer inside a pipe are similar to each other.

3. Mass transfer for flow inside wetted-wall towers

When a gas is flowing inside the core of a wetted-wall tower, the same correlations that are used for mass transfer of a gas in laminar or turbulent flow in a pipe are applicable. This means that Eqs. (7.3-24) and (7.3-25) can be used to predict mass transfer for the gas. For the mass transfer in the liquid film flowing down the wetted-wall tower, Eqs. (7.3-22) and (7.3-23) can be used for Reynolds numbers of 4Г/μ as defined by Eq. (2.9-29) up to about 1200, and the theoretically predicted values should be multiplied by about 1.5 because of ripples and other factors. These equations hold for short contact times or Reynolds numbers above about 100 (S1).

EXAMPLE 7.3-1. Mass Transfer Inside a Tube A tube is coated on the inside with naphthalene and has an inside diameter of 20 mm and a length of 1.10 m. Air at 318 K and an average pressure of 101.3 kPa flows through this pipe at a velocity of 0.80 m/s. Assuming that the absolute pressure remains essentially constant, calculate the concentration of naphthalene in the exit air. Use the physical properties given in Example 6.2-4. Solution: From Example 6.2-4, DAB = 6.92 × 10−6 m2/s and the vapor pressure pAi = 74.0 Pa or cAi = pAi/RT = 74.0/(8314.3 × 318) = 2.799 × 10−5 kg mol/m3. For air, from Appendix A.3, μ = 1.932 × 10−5 Pa · s, ρ = 1.114 kg/m3. The Schmidt number is The Reynolds number is Hence, the flow is laminar. Then, Using Fig. 7.3-2 and the rodlike flow line, (cA − cA0)/(cAi − cA0) = 0.55. Also, cA0(inlet) = 0. Then, (cA − 0)/(2.799 × 10−5 − 0) = 0.55. Solving cA (exit concentration) = 1.539 × 10−5 kg mol/m3.

7.3E. Mass Transfer for Flow Outside Solid Surfaces

1. Mass transfer in flow parallel to flat plates

The mass transfer and vaporization of liquids from a plate or flat surface to a flowing stream is of interest in the drying of inorganic and biological materials, in the evaporation of solvents from paints, for plates in wind tunnels, and in flow channels in chemical process equipment.

When the fluid flows past a plate in a free stream in an open space the boundary layer is not fully developed. For gases or evaporation of liquids in the gas phase and for the laminar region of N_Re,L = Lνρ/μ less than 15 000, the data can be represented within ±25% by the equation (S4)

Equation 7.3-26

Writing Eq. (7.3-26) in terms of the Sherwood number N_Sh,

Equation 7.3-27

where L is the length of plate in the direction of flow. Also, J_D = J_H = f/2 for this geometry. For gases and N_Re,L of 15 000–300 000, the data are represented within ±30% by J_D = J_H = f/2 as

Equation 7.3-28

Experimental data for liquids are correlated within about ±40% by the following for a N_Re,L of 600–50 000 (L2):

Equation 7.3-29

EXAMPLE 7.3-2. Mass Transfer from a Flat Plate A large volume of pure water at 26.1°C is flowing parallel to a flat plate of solid benzoic acid, where L = 0.244 m in the direction of flow. The water velocity is 0.061 m/s. The solubility of benzoic acid in water is 0.02948 kg mol/m3. The diffusivity of benzoic acid is 1.245 × 10−9 m2/s. Calculate the mass-transfer coefficient kL and the flux NA. Solution: Since the solution is quite dilute, the physical properties of water at 26.1°C from Appendix A.2 can be used: The Schmidt number is The Reynolds number is Using Eq. (7.3-29), The definition of JD from Eq. (7.3-5) is Equation 7.3-5 Solving for . Substituting known values and solving, In this case, diffusion is for A through nondiffusing B, so kc in Eq. (7.2-10) should be used: Equation 7.2-10 Since the solution is very dilute, xBM ≅ 1.0 and Also, cA1 = 2.948 × 10−2 kg mol/m3 (solubility) and cA2 = 0 (large volume of fresh water). Substituting into Eq. (7.2-10),

2. Mass transfer for flow past single spheres

For flow past single spheres and for very low N_Re = D_ρνρ/μ, where ν is the average velocity in the empty test section before the sphere, the Sherwood number, which is , should approach a value of 2.0. This can be shown from Eq. (6.2-33), which was derived for a stagnant medium. Rewriting Eq. (6.2-33) as follows, where D_p is the sphere diameter,

Equation 7.3-30

The mass-transfer coefficient k_c, which is for a dilute solution, is then

Equation 7.3-31

Rearranging,

Equation 7.3-32

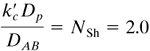
Of course, natural convection effects could increase .

For gases, for a Schmidt number range of 0.6–2.7 and a Reynolds number range of 1–48 000, a modified equation (G1) can be used:

Equation 7.3-33

This equation also holds for heat transfer, where the Prandtl number replaces the Schmidt number and the Nusselt number hD_p/k replaces the Sherwood number.

For liquids (G3) and a Reynolds number range of 2 to about 2000, the following can be used:

Equation 7.3-34

For liquids and a Reynolds number of 2000–17 000, the following can be used (S5):

Equation 7.3-35

EXAMPLE 7.3-3. Mass Transfer from a Sphere Calculate the value of the mass-transfer coefficient and the flux for mass transfer from a sphere of naphthalene to air at 45°C and 1 atm abs flowing at a velocity of 0.305 m/s. The diameter of the sphere is 25.4 mm. The diffusivity of naphthalene in air at 45°C is 6.92 × 10−6 m2/s and the vapor pressure of solid naphthalene is 0.555 mm Hg. Use English and SI units. Solution: In English units DAB = 6.92 × 10−6(3.875 × 104) = 0.2682 ft2/h. The diameter Dp = 0.0254 m = 0.0254(3.2808) = 0.0833 ft. From Appendix A.3 the physical properties of air will be used, since the concentration of naphthalene is low: The Schmidt number is The Reynolds number is Equation (7.3-33) for gases will be used: From Eq. (7.3-3), Substituting the knowns and solving, From Table 7.2-1, Hence, for T = 45 + 273 = 318 K = 318(1.8) = 574°R, Since the gas is very dilute, yBM ≅ 1.0 and . Substituting into Eq. (7.2-12) for A diffusing through stagnant B and noting that pA1 = 0.555/760 = 7.303 × 10−4 atm = 74.0 Pa and pA2 = 0 (pure air), The area of the sphere is Total amount evaporated = NA A = (1.18 × 10−4)(2.18 × 10−2) = 2.572 × 10−6 lb mol/h = (1.599 × 10−7)(2.025 × 10−3) = 3.238 × 10−10 kg mol/s

3. Mass transfer to packed beds

Mass transfer to and from packed beds occurs often in processing operations, including drying operations, adsorption or desorption of gases or liquids by solid particles such as charcoal, and mass transfer of gases and liquids to catalyst particles. By using a packed bed a large amount of mass-transfer area can be contained in a relatively small volume.

The void fraction in a bed is ε m³ volume void space divided by the m³ total volume of void space plus solid. The values range from 0.3 to 0.5 in general. Because of flow channeling, nonuniform packing, and so forth, accurate experimental data are difficult to obtain and data from different investigators can deviate considerably.

For a Reynolds number range of 10–10 000 for gases in a packed bed of spheres (D4), the recommended correlation with an average deviation of about ±20% and a maximum of about ±50% is

Equation 7.3-36

It has been shown (G4, G5) that J_D and J_H are approximately equal. The Reynolds number is defined as N_Re = D_pν'ρ/μ, where D_p is diameter of the spheres and ν' is the superficial mass average velocity in the empty tube without packing. For Eqs. (7.3-36)–(7.3-39) and Eqs. (7.3-5)–(7.3-6), ν' is used.

For mass transfer of liquids in packed beds, the correlations of Wilson and Geankoplis (W1) should be used. For a Reynolds number D_pν'ρ/μ range of 0.0016–55 and a Schmidt number range of 165–70 000, the equation to use is

Equation 7.3-37

For liquids and a Reynolds number range of 55–1500 and a Schmidt number range of 165–10 690,

Equation 7.3-38

Or, as an alternate, Eq. (7.3-36) can be used for liquids for a Reynolds number range of 10–1500.

For fluidized beds of spheres, Eq. (7.3-36) can be used for gases and liquids and a Reynolds number range of 10–4000. For liquids in a fluidized bed and a Reynolds number range of 1–10 (D4),

Equation 7.3-39

If packed beds of solids other than spheres are used, approximate correction factors can be used with Eqs. (7.3-36)–(7.3-38) for spheres. This is done, for example, for a given nonspherical particle as follows. The particle diameter to use in the equations for predicting J_D is the diameter of a sphere with the same surface area as the given solid particle. The flux to these particles in the bed is then calculated using the area of the given particles. An alternative approximate procedure is given elsewhere (G6).

4. Calculation method for packed beds

To calculate the total flux in a packed bed, J_D is first obtained and then k_c in m/s from the J_D. Then, knowing the total volume V_b m³ of the bed (void plus solids), the total external surface area A m² of the solids for mass transfer is calculated using Eqs. (7.3-40) and (7.3-41):

Equation 7.3-40

where a is the m² surface area/m³ total volume of bed when the solids are spheres, and

Equation 7.3-41

To calculate the mass-transfer rate, the log mean driving force at the inlet and outlet of the bed should be used:

Equation 7.3-42

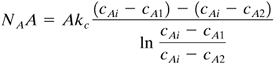
where the final term is the log mean driving force: c_Ai is the concentration at the surface of the solid, in kg mol/m³; c_A1 is the inlet bulk fluid concentration; and c_A2 is the outlet. The material-balance equation on the bulk stream is

Equation 7.3-43

where V is volumetric flow rate of fluid entering in m³/s. Equations (7.3-42) and (7.3-43) must both be satisfied. The use of these two equations is similar to the use of the log mean temperature difference and heat balance in heat exchangers. These two equations can also be used for a fluid flowing in a pipe or past a flat plate, where A is the pipe wall area or plate area.

EXAMPLE 7.3-4. Mass Transfer of a Liquid in a Packed Bed Pure water at 26.1°C flows at the rate of 5.514 × 10−7 m3/s through a packed bed of benzoic-acid spheres having a diameter of 6.375 mm. The total surface area of the spheres in the bed is 0.01198 m2 and the void fraction is 0.436. The tower diameter is 0.0667 m. The solubility of benzoic acid in water is 2.948 × 10−2 kg mol/m3. Predict the mass-transfer coefficient kc. Compare with the experimental value of 4.665 × 10−6 m/s by Wilson and Geankoplis (W1). Using the experimental value of kc, predict the outlet concentration of benzoic acid in the water. Solution: Since the solution is dilute, the physical properties of water will be used at 26.1°C from Appendix A.2. At 26.1°C, μ = 0.8718 × 10−3 Pa · s, ρ = 996.7 kg/m3. At 25.0°C, μ = 0.8940 × 10−3 Pa · s, and from Table 6.3-1, DAB = 1.21 × 10−9 m2/s. To correct DAB to 26.1°C using Eq. (6.3-9), . Hence, The tower cross-sectional area = (π/4)(0.0667)2 = 3.494 × 10−3 m2. Then ν' = (5.514 × 10−7)/(3.494 × 10−3) = 1.578 × 10−4 m/s. Then, The Reynolds number is Using Eq. (7.3-37) and assuming kc = for dilute solutions, Then, using Eq. (7.3-5) and solving, The predicted = 4.447 × 10−6 m/s. This compares with the experimental value of 4.665 × 10−6 m/s. For part (b), using Eqs. (7.3-42) and (7.3-43), Equation 7.3-44 The values to substitute into Eq. (7.3-44) are cAi = 2.948 × 10−2, cA1 = 0, A = 0.01198, V = 5.514 × 10−7. Solving, cA2 = 2.842 × 10−3 kg mol/m3.

5. Mass transfer for flow past single cylinders

Experimental data have been obtained for mass transfer from single cylinders when the flow is perpendicular to the cylinder. The cylinders are long and mass transfer to the ends of the cylinder is not considered. For the Schmidt number range of 0.6 to 2.6 for gases and 1000 to 3000 for liquids and a Reynolds number range of 50 to 50 000, data from many references (B3, L1, M1, S4, V1) have been plotted, and the correlation to use is as follows:

Equation 7.3-45

The data scatter considerably by up to ±30%. This correlation can also be used for heat transfer, with J_D = J_H.

6. Liquid metals mass transfer

In recent years several correlations for mass-transfer coefficients of liquid metals have appeared in the literature. It has been found (G1) that with moderate safety factors, the correlations for nonliquid metals mass transfer may be used for liquid metals mass transfer. Care must be taken to ensure that the solid surface is wetted. Also, if the solid is an alloy, there may exist a resistance to diffusion in the solid phase.