CHAPTER 6

Group-Theoretic Facts about G_geom and G_arith

Theorem 6.1. Suppose N in P_arith is geometrically semisimple. Then G_geom,N is a normal subgroup of G_arith,N.

Proof. Because N is geometrically semisimple, the group G_geom,N is reductive, so it is the fixer of its invariants in all finite dimensional representations of the ambient G_arith,N. By noetherianity, there is a finite list of representations of G_arith,N such that G_geom,N is the fixer of its invariants in these representations. Taking the direct sum of these representations, we get a single representation of G_arith,N such that G_geom,N is the fixer of its invariants in that single representation. This representation corresponds to an object M in <N>_arith, and a G_geom,N- invariant in that representation corresponds to a δ₁ sitting inside M_geom. So the entire space of G_geom,N-invariants corresponds to the subobject Hom_geom(δ₁, M)⊗δ₁ of M. [This is an arithmetic subobject, of the form (a Gal(k/k)-representation)⊗δ₁.] Thus the space of G_geom,N -invariants is G_arith,N -stable (because it corresponds to an arithmetic subobject of M). But the fixer of any G_arith,N -stable subspace in any representation of G_arith,N is a normal subgroup of G_arith,N.

Theorem 6.2. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). If G_arith,N is finite, then N is punctual. Indeed, if every Frobenius conjugacy class Frob_E,χ in G_arith,N is quasiunipotent (:= all eigenvalues are roots of unity), then N is punctual.

Proof. We argue by contradiction. If N is not punctual, it has a non-punctual irreducible constituent. The G_arith of this constituent is a quotient of G_arith,N which inherits the quasiunipotence property. So we reduce to the case when N is G[1] for an (arithmetically irreducible, but we will not use this) middle extension sheaf G which is pure of weight –1. As every Frob_E,χ is quasiunipotent, in particular it has unitary eigenvalues, so every fibre functor !_χ is pure of weight zero, and hence every χ is good for N, and its fibre functor is just

!_χ(M) ≅ H⁰_c(G/k, M ⊗L_χ).

On some dense open set U ⊂ G, G|U is a lisse sheaf on U, pure of weight –1 and of some rank r ≥ 1. For any large enough finite field extension E/k, U(E) is nonempty. Pick such an E/k of even degree, and a point a ∈ U(E). For each character χ of G(E) ≅ E^×, we have

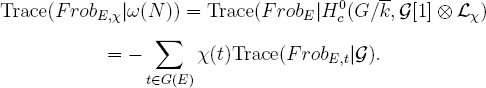
By multiplicative Fourier inversion, we get

And for the finite extension E_n/E of degree n, we get

For each n, #G(E_n) = (#E)ⁿ – 1. So in terms of the r eigenvalues α₁, …, α_r of Frob_E,a|G, we find that for every n ≥ 1, the quantity

is a cyclotomic integer (because each Frob_En,χ|!(N) is quasiunipotent).

From the relation of the first r Newton symmetric functions to the standard ones, we see that the characteristic polynomial of Frob_E,a|G has coefficients in some cyclotomic field, call it L. Hence all Newton symmetric functions of the α_i lie in L. Now consider the rational function of one variable T,

where the coefficients A_n = –((#E)ⁿ – 1)(∑_i(α_i)ⁿ) are, on the one hand, cyclotomic integers, and on the other hand lie in the fixed cyclotomic field L. Therefore the A_n lie in O_L, the ring of integers in L. Therefore the power series around 0 for this rational function converges λ-adically in |T |_λ < 1, for every nonarchimedean place λ of any algebraic closure of L.

By purity, each α_i has complex absolute value 1/√#E, and hence for all i, j we have α_i ≠ (#E)α_j. So there is no cancellation in the expression

of our rational function. Hence for each i, 1/α_i is a pole. Therefore we have

|1/α_i|_λ ≥ 1

for each nonarchimedean λ, which is to say

|α_i|_λ ≤ 1

for each nonarchimedean λ. Thus each α_i is an algebraic integer (in some finite extension of L). But every archimedean absolute value of α_i is 1/√#E < 1. This violates the product formula, and so achieves the desired contradiction.

Corollary 6.3. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). Suppose further that its Tannakian determinant M := “det”(N) has G_geom,M finite. If the group G_arith,N/(G_arith,N ∩ scalars) is finite, then N is punctual. Indeed, if every Frobenius conjugacy class Frob_E,χ in G_arith,N has a power which has all equal eigenvalues, then N is punctual.

Proof. M := “det”(N) is a one-dimensional object, i.e., an object of <N>_arith with χ(G_m/k, M) = 1. One knows [Ka-ESDE, 8.5.3] that the only such objects on G/k ≅ G_m/k are either punctual objects δ_a for some a ∈ G(k), or are multiplicative translates of hypergeometric sheaves H(Ã, χ₁, …, χ_n; ρ₁, …, ρ_m)[1], where Max(n, m) ≥ 1 and where, for all i, j, we have χ_i ≠ ρ_j. But such a hypergeometric sheaf has its G_geom equal to the group GL(1). Indeed, by [Ka-ESDE, 8.2.3] and [Ka-ESDE, 8.4.2 (5)], for any integer r ≥ 1, the r-fold middle convolution of H(Ã, χ₁, …, χ_n; ρ₁, …, ρ_m)[1] with itself is the hypergeometric sheaf of type (rn, rm) given by

H(Ã, each χ_i repeated r times; each ρ_j repeated r times)[1].

Thus no Tannakian tensor power of H(Ã, χ₁, …, χ_n; ρ₁, …, ρ_m)[1] is trivial, so its G_geom must be the entire group GL(1).

Therefore M, having finite G_geom, is geometrically some δ_a, forsome a ∈ G(k). But M lies in <N>_arith, so we must have a ∈ G(k), and M is arithmetically α^deg ⊗ δ_a, for some unitary α.

The statement to be proven, that N is punctual, is a geometric one. And our hypotheses remain valid if we pass from k to any finite extension field E/k. Doing so, we may reduce to the case when G/k is split. Let us denote by d = “dim”N := χ(G_m/k, N) the “dimension” of N. Choose a d’th root β of 1/α, and a d’th root b of 1/a in some finite extension field of k. Again extending scalars, we may reduce to the case when b ∈ k^×. Now consider the object N_?mid (β^deg ⊗ δ_b), on G/k. This object satisfies all our hypotheses, but now its determinant is arithmetically trivial. So if every Frob_E,χ has a power with equal eigenvalues, those equal eigenvalues must be d’th roots of unity, since the determinant is 1. Hence every Frob_E,χ is quasiunipotent, and we conclude by the previous result that N_?mid β^deg ⊗δ_b is punctual. Hence N itself is punctual.

Theorem 6.4. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). If G_geom,N is finite, then N is punctual.

Proof. We argue by contradiction. If N is not punctual, it has some arithmetically irreducible constituent M which is not punctual. Then G_geom,M is finite, being a quotient of G_geom,N. So we are reduced to the case when M is arithmetically irreducible, of the form G[1] for an arithmetically irreducible middle extension sheaf G.

We wish to reduce further to the case in which G is geometrically irreducible. Think of G as the extension by direct image of an arithmetically irreducible lisse sheaf F on a dense open set U ⊂ G. If F|π^geom₁(U)is M n_iF_i, with the F_i inequivalent irreducible representations of π^geom₁(U), then π^arith₁(U) must transitively permute the iso-typical components n_iF_i. Passing to a finite extension field E/k, we reduce to the case when each isotypical component n_iF_i is a π^arith₁(U)-representation.

Passing to one isotypical component, we reduce to the case when N is geometrically G[1] for a middle extension sheaf G, itself the extension by direct image of a lisse sheaf F on U/k such that F = nF₁ is geometrically isotypical. Because we have extended scalars, F may not be arithmetically irreducible, but each of its arithmetically irreducible constituents is itself geometrically isotypical, of the form nF₁ for some possibly lower value of n. So it suffices to treat the case in which F is both arithmetically irreducible and geometrically isotypical (i.e., geometrically nF₁ for some geometrically irreducible F₁ and some n ≥ 1). We claim that in fact n = 1, i.e., that F is geometrically irreducible. To see this, we argue as follows. Consider the dense subgroup Γ of π^arith₁(U) is given by the semidirect product Γ := π^geom₁(U) F^Z, where we take for F an element of degree one in π^arith₁(U). Because Γ is dense in π^arith₁(U), F is Γ-irreducible. So the isomorphism class of F₁ must be invariant by Γ. In other words, F₁ is a representation of π^geom₁(U) whose isomorphism class is invariant by F, and hence F₁ admits a structure of Γ-representation. As representations of Γ, we have

F ≅ F₁ ⊗ Hom_geom(F₁, F).

Here Hom_geom(F₁, F) is an F^Z-representation. It must be irreducible, because F is Γ-irreducible. But n = dimHom_geom(F₁, F), hence n = 1 (because every irreducible representation of the abelian group F^Z has dimension one). Therefore F itself is geometrically irreducible, and so G[1] is geometrically irreducible.

So our situation is that we have an object N = G[1] which is both arithmetically and geometrically irreducible, pure of weight zero, and whose G_geom,N is finite. Therefore its Tannakian determinant M := det(N) has G_geom, M finite. Now G_geom,N acts irreducibly in the representation corresponding to N. But G_geom,N is normal in G_arith,N, so every element of G_arith,N normalizes the finite irreducible group G_geom,N. But Aut(G_geom,N) is certainly finite, so a (fixed) power of every element in G_arith,N commutes with the irreducible group G_geom,N, so is scalar. In particular, each Frob_E,χ has a power which is scalar. The desired contradiction then results from the previous Corollary 6.3.

Theorem 6.5. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). Then the group G_geom,N/G⁰_{geom, N} of connected components of G_geom,N is cyclic of some prime to p order n. Its order n is the order of the group

{ζ ∈ k^×|δ_ζ ∈< N >_geom}.

The irreducible punctual objects in < N >_geom are precisely the objects δ_ζ with ζ ∈ μ_n(k).

Proof. Since G_geom,N is normal in G_arith,N, G⁰_geom,N is also normal in G_arith,N. So we may take a faithful representation of the quotient group G_arith,N/G⁰_geom,N ; this is an object M in P_arith which is arithmetically semisimple and pure of weight zero, and whose G_geom,M is given by G_geom,M = G_geom,N/G⁰_{geom, N}. Hence M is punctual, so geometrically a direct sum of finitely many objects δ_ai for various a_i in k^×. But each a_i lies in a finite field, hence the group generated by the a_i is a finite subgroup of k^×, so it is the group μ_n(k) for some prime to p integer n. So the objects in <M>_geom are just the direct sums of finitely many objects δ_ζi, for various ζ_i ∈ μ_n(k), i.e., they are the representations of Z/nZ. But this same M is a faithful representation of the smaller group G_geom,N/G⁰_geom,N. Hence G_geom,N/G⁰_geom,N = Z/nZ, and the irreducible punctual objects in < N >_geom are precisely the objects δ_ζ with ζ ∈ μ_n(k).

Corollary 6.6. Suppose that N in P_arith is arithmetically semisimple and pure of weight zero (i.e., ι-pure of weight zero for every ι). Then G⁰_geom,N, viewed inside G_geom,N, is the fixer of all punctual objects in <N>_geom. In particular, G_geom,N is connected if and only if the only irreducible punctual object in <N>_geom is δ₁.

Proof. Because G⁰_geom,N is normal in the reductive group G_geom,N, it is itself reductive, so is the fixer of its invariants in <N>_geom. We must show that its invariants there are precisely the punctual objects in <N>_geom.

Any punctual object in <N>_geom is a sum of objects δ_ζ, with ζ ∈ k^× (necessarily) a root of unity, so G⁰_geom,N acts trivially on any punctual object in <N>_geom. Conversely, suppose L ∈ <N>_geom is an irreducible object on which G⁰_geom,N acts trivially. We must show that L is punctual. In any case, L, like any irreducible object of <N>_geom, is geometrically a direct factor of some object of <N>_arith, indeed of some direct sum of multiple middle convolutions of N and its Tannakian dual N^∨. So L is geometrically a direct factor of some arithmetically irreducible object M of <N>_arith. If M is punctual, then L is punctual. If M is not punctual, we get a contradiction as follows: if M is not punctual, then it is j_?F[1] for some arithmetically irreducible lisse sheaf on some dense open set j : U ⊂ G. Exactly as in the proof of Theorem 6.4, after a finite extension of the ground field, we reduce to the case when M is geometrically irreducible, hence geometrically isomorphic to L. But M is not punctual, so not fixed by G⁰_geom,N, contradiction.