CHAPTER 10

A First Construction of Autodual Objects

These constructions are based on evaluating the sum

more or less precisely. As always, this sum is within O(1/#E) of the sum

which is in turn equal, by the Lefschetz Trace formula [Gr-Rat], to

This sum, by orthogonality, is

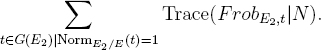
We begin with a geometrically irreducible middle extension sheaf F on G/k which is ι-pure of weight zero, and which is not geometrically an L_χ. Thus F(1/2)[1] is a geometrically irreducible object in P_arith. Its dual in P_arith is [x 1/x] ^?F(1/2)[1], for F the linear dual middle extension sheaf. Via ι, F and F have complex conjugate trace functions; this holds by ι-purity on the dense open set where F is lisse, and then on all of G by a result of Gabber [Fuj-Indep, Thm. 3], cf. also [Ka-MMP, proof of 1.8.1 (i)].

Theorem 10.1. Suppose that the tensor product sheaf

G := F ⊗ [x 1/x] ^?F

is itself a middle extension sheaf; this is automatic if either F is lisse on G or if the finite set S of points of G(k) at which F is ramified is disjoint from the set 1/S of its inverses. Suppose further that G is geometrically irreducible, and not geometrically isomorphic to an L_χ. Then G(1/2)[1] is a geometrically irreducible object of P_arith which is symplectically self-dual.

Proof. It is obvious from the description of the dual of an object N of P_arith as [x 1/x]^? DN that G(1/2)[1] is arithmetically self-dual. The sign of the autoduality is given approximately by the sum

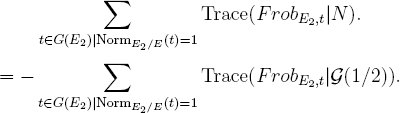
Because we are taking Frobenii over E₂, the 1/2 Tate twist pulls out a factor 1/#E, so this last sum is

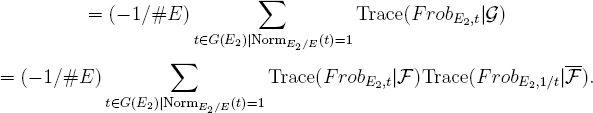
The key observation is that for t ∈ G(E₂) with Norm_E2/E(t) = 1, we have 1/t = σ(t) for σ the nontrivial element in Gal(E₂/E). Thus

Trace(Frob_{E2, 1/t}|F) = Trace(Frob_{E2, σ(t)}|F)

for such a t. On the other hand, since F starts life on G/k, we have

Trace(Frob_{E2, σ(t)}|F) = Trace(Frob_{E2, t}|F),

which is in turn equal to

Trace(Frob_{E2, t}|F).

So our sum is

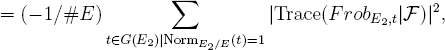
which is negative or zero. But for large #E this sum is approximately the sign, which is ±1, so for large #E the sum cannot vanish, so must be strictly negative. Hence the sign ², which is ±1, must be –1.