3.2.1.1 Invariant laws, stationary chain, and balance equations

Let be a Markov chain with matrix , and be its instantaneous laws. Then, solves the linear (or affine) recursion and, under weak continuity assumptions, can converge to some law only if is a fixed point for the recursion, and hence only if .

If a law is s.t. , and if , then

and hence, is a Markov chain with matrix and initial law and thus has same law as . The chain is then said to be in equilibrium or stationary, and is said to be its invariant law or stationary distribution.

In order to search for an invariant law, three main steps must be followed in order.

1. Solve the linear equation .
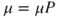2. Find which solutions are nonnegative and nonzero. Such a solution is called an invariant measure.
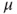3. For any such invariant measure , check whether 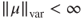(always true if 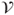is finite), and if so normalize 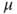to obtain an invariant law .

The linear equation for the invariant measure can be written in a number of equivalent ways, among which . It is practical to use such condensed abstract notations for the invariant measure equation, but it is important to be able to write it as a system if one wants to solve it, for instance as follows.

Global balance (or equilibrium) equations

This is the linear system

3.2.4

It can be interpreted as a balance equation on the graph between all which “leaves” and all which “enters” , in strict sense.

The same balance reasoning taken in wide sense yields , and we obtain this equivalent version of the invariant measure equation using that . If is an invariant measure then, for every subset of , the balance equation

holds for what leaves and enters it. The simple proof is left as an exercise.

As in all developed expressions for , the global balance system is in general highly coupled and is very difficult to solve. This is why the following system is of interest.

Local balance (or equilibrium) equations

This is the linear system

3.2.5

It can be interpreted as a balance equation on the graph between all which goes from to and all which goes from to .

By summing over , we readily check that any solution of (3.2.5) is a solution of (3.2.4), but the converse can easily be seen to be false. This system is much less coupled and simpler to solve that the global balance, and often should be tried first, by it often has only the null solution.

This system is also called the detailed balance equations, as well as the reversibility equations, and the latter terminology will be explained later.

3.2.1.2 Uniqueness, superinvariant measures, and positivity

The space of invariant measures constitutes a positive cone (without the origin).

An invariant measure is said to be unique if it is so up to a positive multiplicative constant, that is, if this space is reduced to the half-line generated by . Then, if , then is the unique invariant law or else if then there is no invariant law.

A measure is said to be superinvariant if and . Note that any invariant measure is superinvariant. This notion will be helpful for the uniqueness results. We use the classic conventions for addition and multiplication in (see Section A.3.3).

3.2.3.1 Finite state space

The following simple corollary is very important in practice and can readily be proved directly.

3.2.3.2 Mean return time in a finite set

We give an extension of this result, which is quite useful for certain positive recurrence criteria.

3.2.4.1 Nearest-neighbor walk in one dimension

The nearest-neighbor random walk on with probability of going to the right and of going to the left is an irreducible Markov chain (see Section 3.1.3). The local balance equations are given by

and have solution . The global balance equations are given by

and this second-order linear recursion has characteristic polynomial

with roots and , possibly equal.

If , then the invariant measures are of the form for all and s.t. . There is nonuniqueness of the invariant measure, and Theorem 3.2.3 yields that the random walk is transient.

If , then the general solution for the global balance equation is , and the nonnegative solutions are of constant equal to . Hence, the uniform measure is the unique invariant measure, and as it is of infinite mass there is no invariant law. The invariant law criterion (Theorem 3.2.4) yields that this chain is not positive recurrent.

In Section 3.1.3, we have used the study of the unilateral hitting time to prove that for the chain is recurrent, and hence, it is null recurrent.

We have given examples, when in which there is nonuniqueness of the invariant measure, and when in which the uniqueness result in Theorem 3.2.3 requires the nonnegativity assumption.

3.2.4.2 Symmetric random walk in many dimensions

For the symmetric random walk on for , the unique invariant measure is uniform. As it has infinite mass, there is no invariant law. The invariant law criterion (Theorem 3.2.4) yields that this chain is not positive recurrent.

We have used the Potential matrix criterion in Section 3.1.3 to prove that in dimension and the random walk is recurrent, and hence null recurrent, whereas in dimension it is transient.

3.2.4.3 Nearest-neighbor walk in one dimension reflected at 0

Let us consider the random walk on reflected at , for which and for and at the boundary and , with graph

Two cases of particular interest are and .

The global balance equations are given by

Hence, and then , and clearly the recursion then determines for , so that there is uniqueness of the invariant measure.

The values for could be determined under the general form if or if , by determining and using the values for and , but it is much simpler to use the local balance equations.

The local balance equations are

and thus and for , and hence,

For , this is a geometric sequence.

If , then and the invariant law criterion (Theorem 3.2.4) yields that the chain is positive recurrent. For ,

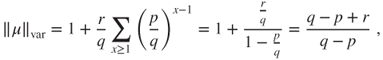
and the unique invariant law is given by . For , it holds that

and for we obtain the geometric law for .

If , then this measure has infinite mass, and the chain cannot be positive recurrent. The results on the unilateral hitting time, or on the nearest-neighbor random walk on , yield that the chain is null recurrent if and transient if .

3.2.4.4 Ehrenfest Urn

See Section 1.4.4. The chains on and on are irreducible, and Corollary 3.2.7 yields that they are positive recurrent.

We have seen that the invariant law of is the uniform law on , and deduced from this that the invariant law of is binomial , given by

We also can recover the invariant law of by solving the local balance equation, given by

see (1.4.4), and hence,

Finding the invariant law reduces now to computing the normalizing constant

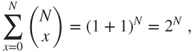
and we again find that .

Such a normalizing problem happens systematically, and may well be untractable, be it the computation of an infinite sum or of a huge combinatorial finite sum.

Mean time to return to vacuum

Starting at , the mean waiting time before compartment is empty again is given by

This is absolutely enormous for of the order of the Avogadro's number. Compared to it, the duration of the universe is absolutely negligible (in an adequate timescale).

Mean time to return to balanced state

Consider state , which is a well-balanced state. It is the mean value of in equilibrium if is even, or else the nearest integer below it. According to whether is even or odd,

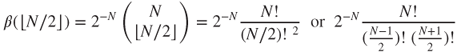
and the Stirling formula yields that

3.2.6

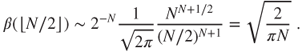
Thus

and is even small compared to the number of molecules , the inverse of which should give the order of magnitude of the time-step.

3.2.4.5 Renewal process

See Section 1.4.5. Assume that is irreducible. A necessary and sufficient condition for to be recurrent is that

and this is also the necessary and sufficient condition for the existence of an invariant measure. We have given an explicit expression for the invariant measure when it exists, and shown that then it is unique.

A necessary and sufficient condition for the existence of an invariant law is that

and we have given an explicit expression for when it exists. By the invariant law criterion, this is also a necessary and sufficient condition for positive recurrence.

All this is actually obvious, as when .

Note that if , then the renewal process is an example of an irreducible Markov chain having no invariant measure.

3.2.4.6 Word search

See Section 1.4.6. The chain is irreducible on a finite state space, so that Corollary 3.2.7 of the invariant law criterion yields that it is positive recurrent. Its invariant law was computed at the end of Section 1.2.

3.2.4.7 Snake chain

See Section 1.4.6, where we proved that if has an invariant law then so does . The invariant law criterion yields that if is irreducible positive recurrent on , then so is on its natural state space . It is clear that if is null recurrent for , then cannot be positive recurrent for , and hence is null recurrent.

3.2.4.8 Product chain

See Section 1.4.7. One must be well aware that and may be irreducible without being so.

The decomposition in recurrent classes and the invariant law criterion yield that if for every state is positive recurrent for , then there exists invariant laws for . Then, is an invariant law for , which is hence positive recurrent.

If for every state is null recurrent for , then may be either transient or null recurrent (see Exercise 3.2).

3.3.1.1 Superharmonic, subharmonic, and harmonic functions

A function on is said to be harmonic if , or equivalently if , that is, if it is an eigenvector of for the eigenvalue . A function is said to be superharmonic if and to be subharmonic if .

Note that a function is subharmonic if and only if is superharmonic and harmonic if and only if is both superharmonic and subharmonic.

The constant functions are harmonic, and a natural question is whether these are the only harmonic functions. Theorem 2.2.2 will be very useful in this perspective, for instance, it yields that

is the least nonnegative superharmonic function, which is larger than on .

This theorem recalls Theorem 3.2.3, and we will develop in Lemma 3.3.9 and thereafter an appropriate duality to deduce one from the other. Care must be taken, as there exists transient transition matrices without any invariant measure, see the renewal process for ; others with a unique invariant measure, see the nearest-neighbor random walks reflected at on ; and others with nonunique invariant laws, see the nearest-neighbor random walks on .

3.3.1.2 Supermartingale techniques

It is instructive to give two proofs of the “only if” part of Theorem 3.3.1 (the most difficult) using supermartingale concepts.

We assume that is nonnegative superharmonic and that is irreducible recurrent. A fundamental observation is that if is a Markov chain and is superharmonic, then is a supermartingale.

Second Proof (J.L. Doob)

This uses more elementary results. Let and be in , and

Then, and the stopped process are supermartingales, and thus

and as by Lemma 3.1.3, the Fatou lemma (Lemma A.3.3) yields that

Hence, is constant, as and are arbitrary.

In this and the following proofs, we have elected to use results in Markov chain theory such as Lemma 3.1.3 as much as possible but could replace them by the Doob convergence theorem to prove convergences.

3.3.2.1 Transience and nonpositive-recurrence criteria

A simple corollary of the “only if” part of Theorem 3.3.1 allows to get rid of a subset of the state space in which the Markov chain behaves “poorly.”

It is a simple matter to adapt the proof using Theorem 2.2.2 or the second supermartingale proof for Theorem 3.3.1, and this is left as an exercise.

Note that and that we may assume that . The functions under consideration are basically upper-bounded subharmonic and nonnegative.

The sequel is an endeavor to replace the upper-bound assumption by integrability assumptions. Let us start with a variant of results due to J. Lamperti.

The next criterion, due to R. Tweedie, uses a submartingale and a direct computation of convergence.

3.3.2.2 Positive recurrence criteria

Such criteria cannot be based on solid results such as Theorem 3.3.1 and are more delicate. We are back to functions that are basically nonnegative superharmonic and to supermartingales.

Theorem 3.3.5 in conjunction with Theorem 3.3.4 provides a null recurrence criterion. Under stronger assumptions, a positive recurrence criterion is obtained.