A.3 Measure-theoretic framework
This appendix introduces without proofs the main notions and results in measure and integration theory, which allow to treat the subject of Markov chains in a mathematically rigorous way.
A.3.1 Probability spaces
A probability space ![]() is given by
is given by
- a set
 encoding all possible random outcomes,
encoding all possible random outcomes, - a
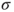 -field
-field 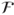 , which is a set constituted of certain subsets of
, which is a set constituted of certain subsets of 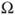 , and satisfies
, and satisfies
- the set
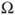 is in
is in 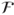 ,
, - if
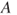 is in
is in 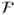 , then its complement
, then its complement 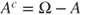 is in
is in 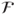 ,
, - if
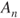 for
for  in
in 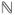 is in
is in  , then
, then  is in
is in 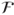 ,
,
- the set
- a probability measure
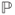 , which is a mapping
, which is a mapping  satisfying
satisfying
- it holds that
 ,
, - the
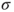 -additivity property: if
-additivity property: if 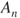 for
for  in
in 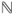 are pairwise disjoint sets of
are pairwise disjoint sets of 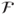 , then
, then

- it holds that
The elements of ![]() are called events, and regroup certain random outcomes leading to situations of interest in such a way that these can be attributed a “likelihood measure” using
are called events, and regroup certain random outcomes leading to situations of interest in such a way that these can be attributed a “likelihood measure” using ![]() .
.
Clearly, ![]() , and
, and ![]() and more generally
and more generally ![]() , and if
, and if ![]() for
for ![]() in
in ![]() is in
is in ![]() , then
, then ![]() . Note that in order to consider finite unions or intersections it suffices to use
. Note that in order to consider finite unions or intersections it suffices to use ![]() or
or ![]() where necessary.
where necessary.
The trivial ![]() -field
-field ![]() is included in any
is included in any ![]() -field, which is in turn included in the
-field, which is in turn included in the ![]() -field of all subsets of
-field of all subsets of ![]() . The latter is often the one of choice when possible, and notably if
. The latter is often the one of choice when possible, and notably if ![]() is countable, but it is often too large to define an appropriate probability measure
is countable, but it is often too large to define an appropriate probability measure ![]() on it. Moreover, the notion of sub-
on it. Moreover, the notion of sub-![]() -field is used to encode partial information available in a probabilistic model.
-field is used to encode partial information available in a probabilistic model.
The following important property is in fact equivalent to ![]() -additivity, using the fact that
-additivity, using the fact that ![]() is a finite measure.
is a finite measure.
A.3.1.1 Generated  -field and information
-field and information
An arbitrary intersection of ![]() -fields is a
-fields is a ![]() -field, and the set of all subsets of
-field, and the set of all subsets of ![]() is a
is a ![]() -field. This allows to define the
-field. This allows to define the ![]() -field generated by a set
-field generated by a set ![]() of subsets of
of subsets of ![]() as the intersection of all
as the intersection of all ![]() -fields containing
-fields containing ![]() , and thus it is the least
, and thus it is the least ![]() -field containing
-field containing ![]() . This
. This ![]() -field is denoted by
-field is denoted by ![]() and encodes the probabilistic information available by observing
and encodes the probabilistic information available by observing ![]() .
.
A.3.1.2 Almost sure (a.s.) and negligible
A subset of ![]() containing an event of probability
containing an event of probability ![]() is said to be almost sure, a subset of
is said to be almost sure, a subset of ![]() included in an event of probability
included in an event of probability ![]() is said to be negligible, and these are two complementary notions. The
is said to be negligible, and these are two complementary notions. The ![]() -additivity property yields that a countable union of negligible events is negligible. By complementation, a countable intersection of almost sure sets is almost sure. A property is almost sure, or holds a.s., if the set of all
-additivity property yields that a countable union of negligible events is negligible. By complementation, a countable intersection of almost sure sets is almost sure. A property is almost sure, or holds a.s., if the set of all ![]() in
in ![]() that satisfy it is almost sure. The classical abbreviation for almost sure is “a.s.” and is often left implicit, but care needs to be taken if a uncountable number of operations are performed.
that satisfy it is almost sure. The classical abbreviation for almost sure is “a.s.” and is often left implicit, but care needs to be taken if a uncountable number of operations are performed.
A.3.2 Measurable spaces and functions: signed and nonnegative
A set ![]() furnished with a
furnished with a ![]() -field
-field ![]() is said to be measurable. A mapping
is said to be measurable. A mapping ![]() from a measurable set
from a measurable set ![]() with
with ![]() -field
-field ![]() to another measurable set
to another measurable set ![]() with
with ![]() -field
-field ![]() is said to be measurable if and only if
is said to be measurable if and only if
A (nonnegative) measure ![]() on a measurable set
on a measurable set ![]() with
with ![]() -field
-field ![]() is a
is a ![]() -additive mapping
-additive mapping ![]() .
.
By ![]() -additivity, if
-additivity, if ![]() and
and ![]() are in
are in ![]() and
and ![]() , then
, then ![]() . The measure
. The measure ![]() is said to be finite if
is said to be finite if ![]() , and then
, and then ![]() , and to be a probability measure or a law if
, and to be a probability measure or a law if ![]() , and then
, and then ![]() .
.
Many results for probability spaces can be extended in this framework (which is usually introduced first) using the classical computation conventions in ![]() .
.
For instance, ![]() if this quantity has a meaning. As in Lemma A.3.1, the
if this quantity has a meaning. As in Lemma A.3.1, the ![]() -additivity property is equivalent to the fact that if
-additivity property is equivalent to the fact that if ![]() is a nondecreasing sequence of events in
is a nondecreasing sequence of events in ![]() , then
, then ![]() . Moreover, by complementation, if
. Moreover, by complementation, if ![]() is a nonincreasing sequence of events in
is a nonincreasing sequence of events in ![]() s.t.
s.t. ![]() for some
for some ![]() , then
, then ![]() .
.
A further extension is given by signed measures ![]() , which are
, which are ![]() -additive mappings
-additive mappings ![]() . The Hahn–Banach decomposition yields an essentially unique decomposition of a signed measure
. The Hahn–Banach decomposition yields an essentially unique decomposition of a signed measure ![]() into a difference of nonnegative finite measures, under the form
into a difference of nonnegative finite measures, under the form ![]() , in which the supports
, in which the supports ![]() and
and ![]() of
of ![]() and
and ![]() are disjoint. The finite nonnegative measure
are disjoint. The finite nonnegative measure ![]() is called the total variation measure of
is called the total variation measure of ![]() , and its total mass
, and its total mass ![]() is called the total variation norm of
is called the total variation norm of ![]() .
.
The space ![]() of all signed measures is a Banach space for this norm, which can be identified with a closed subspace of the strong dual of the functional space
of all signed measures is a Banach space for this norm, which can be identified with a closed subspace of the strong dual of the functional space ![]() .
.
For every (nonnegative, possible infinite) reference measure ![]() , the Banach space
, the Banach space ![]() contains a subspace that can be identified with
contains a subspace that can be identified with ![]() by identifying any measure
by identifying any measure ![]() , which is absolutely continuous w.r.t.
, which is absolutely continuous w.r.t. ![]() with its Radon–Nikodym derivative
with its Radon–Nikodym derivative ![]() . If
. If ![]() is discrete, then a natural and universal choice for
is discrete, then a natural and universal choice for ![]() is the counting measure, and thus
is the counting measure, and thus ![]() can be identified with the collection
can be identified with the collection ![]() and
and ![]() with
with ![]() .
.
A.3.3 Random variables, their laws, and expectations
A.3.3.1 Random variables and their laws
A probability space ![]() is given. A random variable (r.v.) with values in a measurable set
is given. A random variable (r.v.) with values in a measurable set ![]() with
with ![]() -field
-field ![]() is a measurable function
is a measurable function ![]() , which satisfies
, which satisfies
For an arbitrary mapping ![]() , the set
, the set
is a ![]() -field, called the
-field, called the ![]() -field generated by
-field generated by ![]() , encoding the information available on
, encoding the information available on ![]() by observing
by observing ![]() . Notably,
. Notably, ![]() is measurable if and only if
is measurable if and only if ![]() .
.
The probability space ![]() is often only assumed to be fixed without further precision and represents some kind of ideal probabilistic knowledge. Only the properties of certain random variables are precisely given. These often represent indirect observations or effects of the random outcomes, and it is natural to focus on them to get useful information.
is often only assumed to be fixed without further precision and represents some kind of ideal probabilistic knowledge. Only the properties of certain random variables are precisely given. These often represent indirect observations or effects of the random outcomes, and it is natural to focus on them to get useful information.
The law of the r.v. ![]() is the probability measure
is the probability measure ![]() on
on ![]() , which is well defined as
, which is well defined as ![]() is measurable. It is denoted by
is measurable. It is denoted by ![]() or
or ![]() and is given by
and is given by
Then, ![]() is a probability space which encodes the probabilistic information available on the outcomes of
is a probability space which encodes the probabilistic information available on the outcomes of ![]() .
.
A.3.3.2 Expectation for 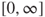 -valued random variables
-valued random variables
The expectation ![]() will be defined as a monotone linear extension of the probability measure
will be defined as a monotone linear extension of the probability measure ![]() , first for random variables taking a finite number of values in
, first for random variables taking a finite number of values in ![]() , then for general random variables with values in
, then for general random variables with values in ![]() , and finally for real random variables satisfying an integrability condition. The notation
, and finally for real random variables satisfying an integrability condition. The notation ![]() is sometimes used to stress
is sometimes used to stress ![]() .
.
This procedure allows to define the integral ![]() of a measurable function
of a measurable function ![]() , from
, from ![]() with
with ![]() -field
-field ![]() to
to ![]() with
with ![]() -field
-field ![]() , by a measure
, by a measure ![]() , but we restrict this to probability measures for the sake of concision.
, but we restrict this to probability measures for the sake of concision.
The classic structure of ![]() is extended to
is extended to ![]() by setting
by setting
Finite number of values
If ![]() is an r.v. taking a finite number of values in
is an r.v. taking a finite number of values in ![]() , then
, then
In particular,
For such random variables, this defines a monotone operator, in the sense that
which moreover is nonnegative linear, in the sense that
Extension by supremum
For an r.v. ![]() with values in
with values in ![]() , let
, let
and
This extension of ![]() is still monotone and nonnegative, from which we deduce the following extension of the monotone limit lemma (Lemma A.3.1). This is where the fact that
is still monotone and nonnegative, from which we deduce the following extension of the monotone limit lemma (Lemma A.3.1). This is where the fact that ![]() is measurable becomes crucial.
is measurable becomes crucial.
Nonnegative linearity
This theorem allows to prove that ![]() is nonnegative linear, by replacing the supremum in the definition by the limit of an adequate nondecreasing sequence. If
is nonnegative linear, by replacing the supremum in the definition by the limit of an adequate nondecreasing sequence. If ![]() is a
is a ![]() -valued r.v., then we define for
-valued r.v., then we define for ![]() the dyadic approximation
the dyadic approximation ![]() satisfying
satisfying
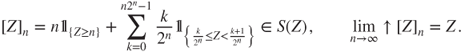
If ![]() and
and ![]() are
are ![]() -r.v., and
-r.v., and ![]() , then
, then
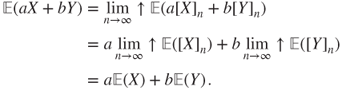
Fatou's Lemma
An important corollary of the monotone convergence theorem is the following.
Let us finish with a quite useful result.
A.3.3.3 Real-valued random variables and integrability
Let ![]() be an r.v. with values in
be an r.v. with values in ![]() . Let
. Let
so that
The natural extension to ![]() of the operations on
of the operations on ![]() lead to setting, except if the indeterminacy
lead to setting, except if the indeterminacy ![]() occurs,
occurs,
This definition is monotone and linear: if all is well defined in ![]() , then
, then
A.3.3.4 Integrable random variables
In particular,
and the latter is well defined. This is the most useful case and is extended by linearity to define ![]() for
for ![]() with values in
with values in ![]() satisfying
satisfying ![]() for some (and then every) norm
for some (and then every) norm ![]() . Then,
. Then, ![]() is said to be integrable. The integrable random variables form a vector space
is said to be integrable. The integrable random variables form a vector space
It is a simple matter to check that if ![]() is an r.v. with values in
is an r.v. with values in ![]() and
and ![]() is measurable then
is measurable then
in all cases in which one of these expressions can be defined, and then all can.
The expectation has good properties w.r.t. the a.s. convergence of random variables. The monotone convergence theorem has already been seen. Its corollary the Fatou lemma will be used to prove an important result.
A sequence of ![]() -valued random variables
-valued random variables ![]() is said to be dominated by an r.v.
is said to be dominated by an r.v. ![]() if
if
and to be dominated in ![]() by
by ![]() if moreover
if moreover ![]() . The sequence is thus dominated in
. The sequence is thus dominated in ![]() if and only if
if and only if
This theorem can be extended to the case when
Indeed, the Borel–Cantelli lemma implies that then, from each subsequence, a further subsubsequence converging a.s. can be extracted. Applying Theorem A.3.5 to this a.s. converging sequence yields that the only accumulation point in ![]() for
for ![]() is
is ![]() , and hence that
, and hence that ![]() .
.
A.3.3.5 Convexity inequalities and 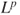 spaces
spaces
For ![]() , we will check that the set of all
, we will check that the set of all ![]() -valued random variables
-valued random variables ![]() s.t.
s.t. ![]() forms a Banach space, denoted by
forms a Banach space, denoted by
if two a.s. equal random variables are identified (i.e., on the quotient space). In particular, ![]() is a Hilbert space with scalar product
is a Hilbert space with scalar product
This proof remains valid if ![]() is replaced by an arbitrary positive measure. The case
is replaced by an arbitrary positive measure. The case ![]() is a special case of the Cauchy–Schwarz inequality.
is a special case of the Cauchy–Schwarz inequality.
The Jensen inequality yields that if ![]() , then
, then ![]() . The linear form
. The linear form ![]() hence has operator norm
hence has operator norm ![]() , as
, as
with equality for constant ![]() .
.
A.3.4 Random sequences and Kolmogorov extension theorem
Let us go back to Section 1.1. Let be given a family of laws ![]() on
on ![]() , for
, for ![]() and
and ![]() in
in ![]() . Two natural questions arise:
. Two natural questions arise:
- Does there exist a probability space
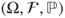 , a
, a 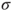 -field on
-field on 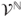 , and an r.v.
, and an r.v.  , satisfying that
, satisfying that

that is, this family of laws are the finite-dimensional marginals of
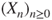 ?
? - If it is so, is the law of
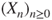 unique, that is, is it characterized by its finite-dimensional marginals?
unique, that is, is it characterized by its finite-dimensional marginals?
Clearly, the ![]() must be consistent, or compatible: if
must be consistent, or compatible: if ![]() is a
is a ![]() -tuple included in the
-tuple included in the ![]() -tuple
-tuple ![]() , then
, then ![]() must be equal to the corresponding marginal of
must be equal to the corresponding marginal of ![]() .
.
It is natural and “economical” to take ![]() , called the canonical space, the process
, called the canonical space, the process ![]() given by the canonical projections
given by the canonical projections
called the canonical process, and to furnish ![]() with the smallest
with the smallest ![]() -field s.t. each
-field s.t. each ![]() and hence each
and hence each ![]() is an r.v.: the product
is an r.v.: the product ![]() -field
-field
Note that if ![]() is a sequence of subsets of the discrete space
is a sequence of subsets of the discrete space ![]() , then
, then
and that events of this form are sufficient to characterize convergence in results such as the pointwise ergodic theorem (Theorem 4.1.1). See also Section 2.1.1.
By construction, ![]() is measurable and hence an r.v. on
is measurable and hence an r.v. on ![]() furnished with the product
furnished with the product ![]() -field, and if this space is furnished with a probability measure
-field, and if this space is furnished with a probability measure ![]() , then
, then ![]() has law
has law ![]() .
.
The following result is fundamental. It is relatively easy to show the uniqueness part: any two laws on the product ![]() -field with the same finite-dimensional marginals are equal. The difficult part is the existence result, which relies on the Caratheodory extension theorem.
-field with the same finite-dimensional marginals are equal. The difficult part is the existence result, which relies on the Caratheodory extension theorem.
The explicit form given in Definition 1.2.1, in terms of the initial law and the transition matrix ![]() , allows to check easily that these probability measures are consistent. The Kolmogorov extension theorem then yields the existence and uniqueness of the law of the Markov chain on the product space. This yields the mathematical foundation for all the theory of Markov chains.
, allows to check easily that these probability measures are consistent. The Kolmogorov extension theorem then yields the existence and uniqueness of the law of the Markov chain on the product space. This yields the mathematical foundation for all the theory of Markov chains.
