Solutions for the exercises
Solutions for Chapter 1
- 1.1 This constitutes a Markov chain on
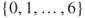 with matrix
with matrix

- from which the graph is readily deduced. The astronaut can reach any module from any module in a finite number of steps, and hence, the chain is irreducible, and as the state space is finite, this yields that there exists a unique invariant measure
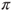 . Moreover,
. Moreover,  and by uniqueness and symmetry,
and by uniqueness and symmetry,  , and hence,
, and hence, 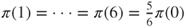 . By normalization, we conclude that
. By normalization, we conclude that  and
and 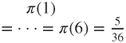 .
.
- 1.2 This constitutes a Markov chain on
 with matrix
with matrix
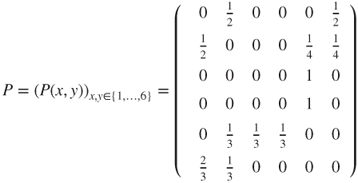
- from which the graph is readily deduced. The mouse can reach one room from any other room in a finite number of steps, and hence, the chain is irreducible, and as the state space is finite, this yields that there exists a unique invariant measure
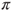 . Solving a simple linear system and normalizing the solution yield
. Solving a simple linear system and normalizing the solution yield  .
.
- 1.3.a The uniform measure is invariant if and only if the matrix is doubly stochastic.
- 1.3.b The uniform measure is again invariant for
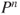 for all
for all 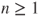 .
.
- 1.3.c Then,
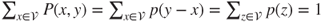 , where
, where 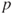 is the law of the jumps.
is the law of the jumps.
- 1.4.a The non zero terms are
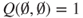 and for
and for 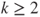 and
and  ,
,
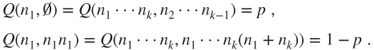
- Any wager lost during the game is inscribed in the list and will be wagered again in the future. When the list is empty, the gambler would have won the initial sum of all the terms on the list
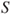 , with the other gains cancelling precisely the losses occurred during the game.
, with the other gains cancelling precisely the losses occurred during the game.
- 1.4.b Then,
 can be written in terms of
can be written in terms of 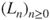 as
as
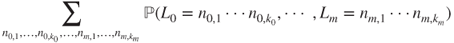
- and the Markov property for
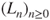 yields that the terms of this sum write
yields that the terms of this sum write
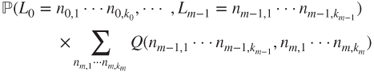
- and hence,

- where the non zero terms of
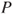 are
are  and
and  for
for  and
and 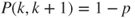 for
for 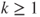 .
.
- 1.5.a A natural state space is the set of permutations of
 , of the form
, of the form  , which has cardinal
, which has cardinal 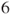 . By definition
. By definition

- Clearly,
 is irreducible. As the state space is finite, this implies existence and uniqueness for the invariant law
is irreducible. As the state space is finite, this implies existence and uniqueness for the invariant law 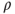 . Intuition (the matrix is doubly stochastic) or solving a simple linear system shows that
. Intuition (the matrix is doubly stochastic) or solving a simple linear system shows that  is the uniform law, with density
is the uniform law, with density  .
.
- 1.5.b A natural state space is the set
 of cardinal
of cardinal  , and
, and
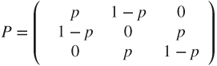
- is clearly irreducible; hence, there is a unique invariant law. The invariant law is the uniform law, with density
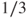 .
.
- 1.5.c The characteristic polynomial of
 is
is
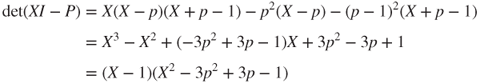
in which
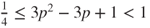 with equality on the left for
with equality on the left for 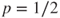 . Hence,
. Hence,  has three distinct roots
has three distinct roots
Hence,
 , where
, where
If
 is even, then
is even, then 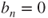 , and
, and 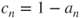 so that
so that 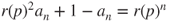 yields
yields 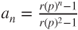 .
.If
 is odd, then
is odd, then 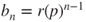 , and
, and 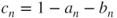 so that
so that  yields
yields 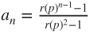 .
.As computing
 is quite simple, this yields an explicit expression for
is quite simple, this yields an explicit expression for 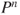 .
.The law of
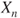 converges to the uniform law at rate
converges to the uniform law at rate 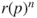 , which is maximal for
, which is maximal for 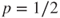 and then takes the value
and then takes the value 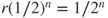 .
. - 1.6 The transition matrix is given by
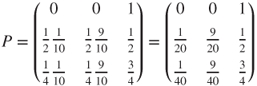
and the graph can easily be deduced from it. Clearly,
 is irreducible. As the state space is finite, it implies that there is a unique invariant law
is irreducible. As the state space is finite, it implies that there is a unique invariant law  . This law solves
. This law solves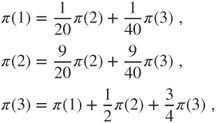
hence
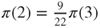 , then
, then  . As
. As 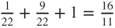 , normalization yields
, normalization yields  ,
, 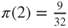 and
and 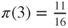 .
.The characteristic polynomial of
 is
is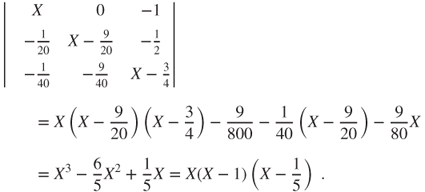
Hence,
 with
with  ,
, 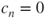 , and
, and  . Thus,
. Thus, 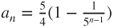 and
and  . The law of
. The law of  converges to
converges to  at rate
at rate  .
. - 1.7.a States
 for
for  ,
,  , and
, and 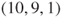 are wins for Player A and states
are wins for Player A and states  for
for 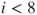 ,
, 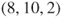 , and
, and 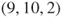 are wins for Player B, and they are the absorbing states.
are wins for Player B, and they are the absorbing states.
Let
 and
and  , or
, or  and
and  .
.Considering all rallies, transitions from
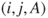 to
to 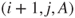 have probability
have probability  , from
, from 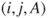 to
to 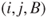 probability
probability  , and symmetrically from
, and symmetrically from 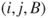 to
to  probability
probability  and from
and from  to
to 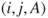 probability
probability 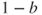 .
.Considering only the points scored, transitions from
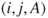 to
to  have probability
have probability 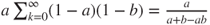 , from
, from  to
to  probability
probability 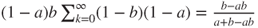 , and symmetrically from
, and symmetrically from 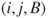 to
to 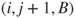 probability
probability  and from
and from 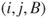 to
to  probability
probability  .
. - 1.7.b Straightforward.
- 1.7.c We use the transition for scored points. Player B wins in
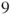 points if he or she scores first, and we have seen that this happens with probability
points if he or she scores first, and we have seen that this happens with probability 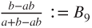 .
.
Player B wins in
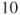 points if Player A scores
points if Player A scores 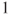 point and then Player B scores
point and then Player B scores 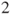 , if Player B scores
, if Player B scores 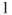 and then Player A scores
and then Player A scores  and then Player B scores
and then Player B scores  , or if Player B scores
, or if Player B scores  points in a row, which happens with probability
points in a row, which happens with probability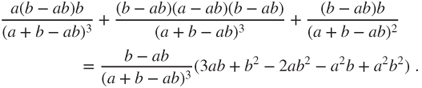
Then,
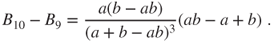
The hyperbole
 divides the square
divides the square 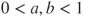 into two subsets. In the first subset, in which
into two subsets. In the first subset, in which  , Player B should go to
, Player B should go to  points (this is the largest subset and contains the diagonal, which is tangent at
points (this is the largest subset and contains the diagonal, which is tangent at  to the hyperbole). In the other, in which
to the hyperbole). In the other, in which  , Player B should go to
, Player B should go to  points.
points. - 1.8.a The microscopic representation
 yields the macroscopic representation
yields the macroscopic representation

- 1.8.b Synchronous: the transition from
 to
to 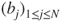 and the transition from
and the transition from 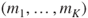 to
to 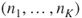 have probabilities
have probabilities

- Asynchronous: for
 , the transition from
, the transition from 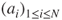 to the vector in which
to the vector in which  is replaced by
is replaced by 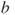 and, for
and, for  , the transition from
, the transition from  if
if  to
to  and if
and if  to the vector in which the
to the vector in which the  th coordinate is replaced by
th coordinate is replaced by 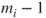 and the
and the  th by
th by 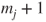 , have probabilities
, have probabilities

- The absorbing states are the pure states, constituting of populations carrying a single allele.
- 1.9.a For instance,
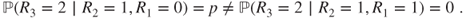
- 1.9.b As then
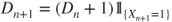 , Theorem 1.(2.3 yields that
, Theorem 1.(2.3 yields that 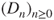 is a Markov chain on
is a Markov chain on 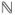 with matrix given by
with matrix given by 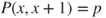 and
and  for
for 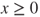 . This matrix is clearly irreducible, but the state space is infinite and we cannot conclude now on existence and uniqueness for invariant law.
. This matrix is clearly irreducible, but the state space is infinite and we cannot conclude now on existence and uniqueness for invariant law.
As an invariant measure,
 , satisfies the equation
, satisfies the equation 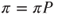 , which develops into
, which develops into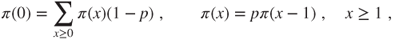
so that necessarily
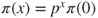 , and we check that
, and we check that 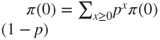 . Moreover,
. Moreover,  and hence,
and hence,  for
for  , which is a geometric law on
, which is a geometric law on 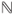 .
. - 1.9.c As
 , Theorem 1.(2.3 yields that
, Theorem 1.(2.3 yields that  is a Markov chain on
is a Markov chain on 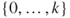 , with matrix given by
, with matrix given by 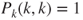 ,
, 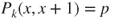 , and
, and 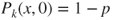 for
for 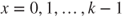 .
. - 1.9.d Then,
 , and as
, and as 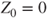 ,
, 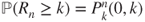 . Hence, for
. Hence, for  ,
,

- 1.9.e This probability is
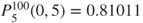 .
. - 1.10.a The non zero terms of
 are
are  for
for  ,
, 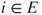 , and
, and 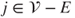 , where
, where 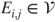 is obtained from
is obtained from 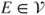 by interchanging
by interchanging  and
and 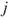 . The matrix is clearly irreducible. As the state space is finite, this implies that there exists a unique invariant law
. The matrix is clearly irreducible. As the state space is finite, this implies that there exists a unique invariant law 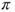 . Intuition (the matrix is doubly stochastic) or a simple computation shows that the uniform law with density
. Intuition (the matrix is doubly stochastic) or a simple computation shows that the uniform law with density 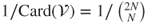 is invariant.
is invariant. - 1.10.b The non zero terms of
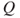 are, for
are, for 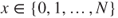 ,
,

- The matrix is clearly irreducible. As the state space is finite, this implies that there exists a unique invariant law
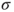 . A combinatorial computation starting from
. A combinatorial computation starting from 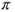 yields that
yields that  for
for  . This is a hypergeometric law.
. This is a hypergeometric law.
- 1.10.c The Markov property yields that

- and this affine recursion is solved by
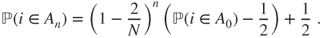
- Moreover,
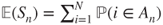 and hence,
and hence,
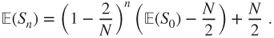
- Then,
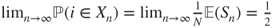 at rate
at rate 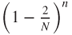 .
.
- 1.11.a Theorem 1.(2.3 yields that this is a Markov chain.
- 1.11.b Computations, quite similar to those for branching, show that
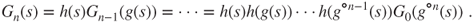
- 1.11.c Similarly, or by a Taylor expansion,

- which takes the value
 if
if  or else
or else 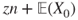 if
if  .
.
- 1.12.a Theorem 1.(2.3 yields that this is a Markov chain. The irreducibility condition is obvious.
- 1.12.b Then,
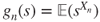 can be written, using independence, as
can be written, using independence, as
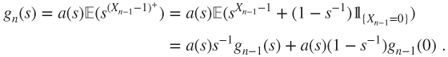
- 1.12.c Then, necessarily
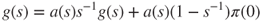
- and thus,
 . For
. For  ,
,
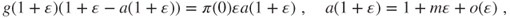
- and identification of the
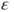 terms yields that
terms yields that  .
.
- 1.12.d As
 , necessarily
, necessarily  , and if
, and if 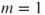 , then
, then  , and the chain cannot be irreducible (as then
, and the chain cannot be irreducible (as then 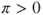 ) and thus
) and thus 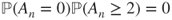 and
and 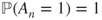 as
as  .
.
- 1.12.e If
 , then
, then
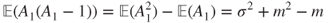
- and hence,
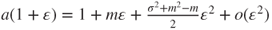 , and using
, and using 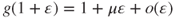 and identifying the terms in
and identifying the terms in  in the above-mentioned Taylor expansion yields that
in the above-mentioned Taylor expansion yields that 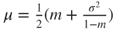 .
.
- 1.13.a By definition and the basic properties of the total variation norm,
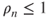 . For all
. For all  and
and 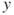 , if
, if  is such that
is such that  , then
, then 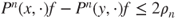 and hence,
and hence,
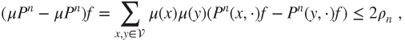
- so that
 .
.
- 1.13.b Then,
 for all laws
for all laws  and
and  , all
, all  such that
such that 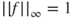 , and all
, and all 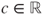 , and
, and
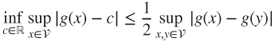
- implies that
 . This yields that
. This yields that 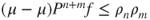 . Then, it is a simple matter to obtain that
. Then, it is a simple matter to obtain that 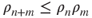 and then that
and then that 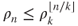 .
.
- 1.13.c Taking
 , it holds that
, it holds that  , which forms a geometrically convergent series, hence classically
, which forms a geometrically convergent series, hence classically  is Cauchy, and as the metric space is complete, there is a limit
is Cauchy, and as the metric space is complete, there is a limit  , which is
, which is 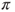 invariant. Then,
invariant. Then,  .
.
- 1.13.d For all
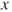 ,
, 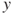 , and
, and  such that
such that 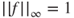 , it holds that
, it holds that 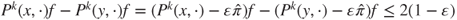 . It is a simple matter to conclude.
. It is a simple matter to conclude.
- 1.13.e For all
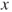 ,
,  , and
, and  such that
such that  , it holds that
, it holds that

- It is a simple matter to conclude.
