3.3.2.3 Queuing application
A system (for instance a processor) processes jobs (such as computations) in synchronized manner. A waiting room (buffer) allows to store jobs before they are processed. The instants of synchronization are numbered ![]() and
and ![]() denotes the number of jobs in the system just after time
denotes the number of jobs in the system just after time ![]() .
.
Between time ![]() and time
and time ![]() , a random number
, a random number ![]() of new jobs arrive, and up to a random number
of new jobs arrive, and up to a random number ![]() of the
of the ![]() jobs already there can be processed, so that
jobs already there can be processed, so that
In a simple special case, there is an integer ![]() s.t.
s.t. ![]() , and it is said that the queue has
, and it is said that the queue has ![]() servers.
servers.
The r.v. ![]() are assumed to be i.i.d. and independent of
are assumed to be i.i.d. and independent of ![]() , and then Theorem 1.2.3 yields that
, and then Theorem 1.2.3 yields that ![]() is a Markov chain on
is a Markov chain on ![]() . We assume that
. We assume that
so that there is a closed irreducible class containing ![]() , and we consider the chain restricted to this class, which is irreducible. We further assume that
, and we consider the chain restricted to this class, which is irreducible. We further assume that ![]() and
and ![]() are integrable, and will see that then the behavior of
are integrable, and will see that then the behavior of ![]() depends on the joint law of
depends on the joint law of ![]() essentially only through
essentially only through ![]() .
.
For ![]() , we have
, we have ![]() and hence,
and hence, ![]() , and
, and ![]() a.s., and
a.s., and ![]() , and thus
, and thus ![]() by dominated convergence (Theorem A.3.5). We deduce a number of facts from this observation.
by dominated convergence (Theorem A.3.5). We deduce a number of facts from this observation.
- If
 , then there exists
, then there exists 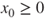 s.t. if
s.t. if 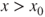 then
then 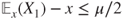 . Then, the Foster criterion (Theorem 3.3.6) with
. Then, the Foster criterion (Theorem 3.3.6) with 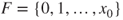 and
and  yields that the chain is positive recurrent, and
yields that the chain is positive recurrent, and  .
. - If
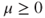 , then the Tweedie criterion (Theorem 3.3.4) with
, then the Tweedie criterion (Theorem 3.3.4) with 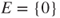 and
and 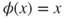 yields that the chain cannot be positive recurrent.
yields that the chain cannot be positive recurrent. - If
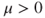 and
and  and
and  are square integrable, then the Lamperti criterion (Theorem 3.3.3) with
are square integrable, then the Lamperti criterion (Theorem 3.3.3) with  and
and 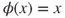 yields that the chain is transient. If only
yields that the chain is transient. If only  is square integrable, then if
is square integrable, then if 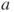 is large enough then
is large enough then
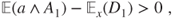
and the chain
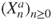 with arrival and potential departures given by
with arrival and potential departures given by 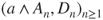 is transient, and as
is transient, and as 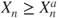 then
then  is transient.
is transient. - If
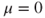 and
and  , then Theorem 3.3.5 with
, then Theorem 3.3.5 with  and
and 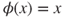 yields that the chain is recurrent, and hence null recurrent.
yields that the chain is recurrent, and hence null recurrent.
3.3.2.4 Necessity of jump amplitude control
In Theorems 3.3.3 and 3.3.4, the hypotheses ![]() are quite natural, but the hypotheses
are quite natural, but the hypotheses ![]() controlling the jump amplitudes cannot be suppressed (but can be weakened).
controlling the jump amplitudes cannot be suppressed (but can be weakened).
We will see this on an example. Consider the queuing system with
Then, ![]() is s.t.
is s.t. ![]() and
and ![]() for
for ![]() and is a random walk on
and is a random walk on ![]() reflected at
reflected at ![]() . For
. For ![]() and
and ![]() with
with ![]() and
and ![]() , it holds that
, it holds that ![]() and
and ![]() and, for
and, for ![]() ,
,
so that hypothesis ![]() of Theorem 3.3.4 is satisfied, and if
of Theorem 3.3.4 is satisfied, and if ![]() , then
, then
so that hypothesis ![]() of Theorem 3.3.3 is satisfied.
of Theorem 3.3.3 is satisfied.
Nevertheless, ![]() and we have seen that
and we have seen that ![]() is positive recurrent for
is positive recurrent for ![]() , null recurrent for
, null recurrent for ![]() , and transient for
, and transient for ![]() .
.
The hypothesis in Theorem 3.3.5 and hypothesis ![]() in Theorem 3.3.6 are also quite natural. The latter is enough to obtain the bound
in Theorem 3.3.6 are also quite natural. The latter is enough to obtain the bound ![]() for
for ![]() , but an assumption such as hypothesis
, but an assumption such as hypothesis ![]() must be made to conclude to positive recurrence. For instance, let
must be made to conclude to positive recurrence. For instance, let ![]() be a Markov chain with matrix
be a Markov chain with matrix ![]() s.t.
s.t.
For ![]() and
and ![]() , it holds that
, it holds that ![]() for
for ![]() , and hypothesis
, and hypothesis ![]() of Theorem 3.3.6 holds, but the chain is null recurrent as
of Theorem 3.3.6 holds, but the chain is null recurrent as
3.3.3 Time reversal, reversibility, and adjoint chain
3.3.3.1 Time reversal in equilibrium
Let ![]() be a Markov chain,
be a Markov chain, ![]() an integer, and
an integer, and ![]() for
for ![]() . Then,
. Then,
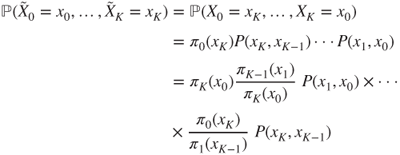
and ![]() corresponds to a time-inhomogeneous Markov chain with transition matrices given by
corresponds to a time-inhomogeneous Markov chain with transition matrices given by
This chain is homogeneous if and only if ![]() is an invariant law, that is, if and only the chain is at equilibrium.
is an invariant law, that is, if and only the chain is at equilibrium.
3.3.3.2 Doubly stationary Markov chain
Let ![]() be a transition matrix with an invariant law
be a transition matrix with an invariant law ![]() . Let
. Let ![]() have law
have law ![]() , let
, let ![]() and
and ![]() be Markov chains of matrices
be Markov chains of matrices ![]() and
and ![]() , which are independent conditional on
, which are independent conditional on ![]() , and let
, and let ![]() . Then,
. Then, ![]() is a stationary Markov chain in time
is a stationary Markov chain in time ![]() with transition matrix
with transition matrix ![]() , called the doubly stationary Markov chain of matrix
, called the doubly stationary Markov chain of matrix ![]() , which can be imagined to be “started” at
, which can be imagined to be “started” at ![]() .
.
3.3.3.3 Reversible measures
The equality ![]() holds if and only if
holds if and only if ![]() solves the local balance equations (3.2.5).
solves the local balance equations (3.2.5).
Then, the chain and its matrix are said to be reversible (in equilibrium), and ![]() to be a reversible law for
to be a reversible law for ![]() . The equations (3.2.5) are also called the reversibility equations and their nonnegative and nonzero solutions the reversible measures.
. The equations (3.2.5) are also called the reversibility equations and their nonnegative and nonzero solutions the reversible measures.
In equilibrium, the probabilistic evolution of a reversible chain is the same in direct or reverse time, which is natural for many statistical mechanics models such as the Ehrenfest Urn.
3.3.3.4 Adjoint chain, superinvariant measures, and superharmonic functions
We gather some simple facts in the following lemma.
This allows to understand the relations between Theorems 3.2.3 and 3.3.1. Let ![]() be an irreducible recurrent transition matrix on
be an irreducible recurrent transition matrix on ![]() and
and ![]() an arbitrary canonical invariant law.
an arbitrary canonical invariant law.
If ![]() is a superinvariant measure for
is a superinvariant measure for ![]() , then the function
, then the function ![]() is nonnegative and superharmonic for
is nonnegative and superharmonic for ![]() , which is irreducible recurrent, and Theorem 3.3.1 yields that
, which is irreducible recurrent, and Theorem 3.3.1 yields that ![]() is constant, that is, Theorem 3.2.3.
is constant, that is, Theorem 3.2.3.
Conversely, if ![]() nonnegative and superharmonic for
nonnegative and superharmonic for ![]() , then
, then ![]() is a superharmonic measure for
is a superharmonic measure for ![]() , and Theorem 3.2.3 yields that
, and Theorem 3.2.3 yields that ![]() is constant, that is, the “only if” part of Theorem 3.3.1.
is constant, that is, the “only if” part of Theorem 3.3.1.
The following result can be useful in the (rare) cases in which a matrix is not reversible, but its time reversal in equilibrium can be guessed.
3.3.4 Birth-and-death chains
A Markov chain on ![]() (or on an interval of
(or on an interval of ![]() ) s.t.
) s.t.
is called a birth-and-death chain. All other terms of ![]() are then zero, this matrix is determined by the Birth-and-death probabilities
are then zero, this matrix is determined by the Birth-and-death probabilities
which satisfy ![]() , and its graph is given by
, and its graph is given by

Several of the examples we have examined are birth-and-death chains: Nearest-neighbor random walks on ![]() , Nearest-neighbor random walks reflected at
, Nearest-neighbor random walks reflected at ![]() on
on ![]() , gambler's ruin, and macroscopic description for the Ehrenfest Urn on
, gambler's ruin, and macroscopic description for the Ehrenfest Urn on ![]() .
.
The chain is irreducible on ![]() if and only if
if and only if
Birth-and-death on  or
or 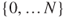
Similarly, ![]() is a closed irreducible class if and only if
is a closed irreducible class if and only if
and ![]() is a closed irreducible class if and only if
is a closed irreducible class if and only if
In these cases, the restriction of the chain is considered. It can be interpreted as describing the evolution of a population that can only increase or decrease by one individual at each step, according to whether there has been a birth or a death of an individual, hence the terminology.
We now give several helpful results, among which a generalization of the gambler's ruin law.
If the birth-and-death chain is irreducible on ![]() for a finite
for a finite ![]() , then it is always positive recurrent, and the invariant law
, then it is always positive recurrent, and the invariant law ![]() is obtained by replacing
is obtained by replacing ![]() by
by ![]() in the formula.
in the formula.
Exercises
Several exercises of Chapter 1 involve irreducibility and invariant laws.
3.1 Generating functions and potential matrix Let ![]() be a Markov chain on
be a Markov chain on ![]() with matrix
with matrix ![]() . For
. For ![]() and
and ![]() in
in ![]() , consider the power series, for
, consider the power series, for ![]() ,
,
- (a) Prove that
 converges for
converges for 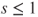 and
and 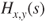 for
for 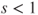 and that
and that

- (b) Prove that
 for
for 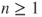 . Prove that,
. Prove that, 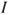 denoting the identity matrix,
denoting the identity matrix,

- (c) Prove that
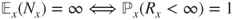 and that if
and that if  and
and  , then
, then  .
. - (d) We are going to apply these results to the nearest-neighbor random walk on
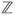 , with matrix given by
, with matrix given by 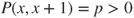 and
and 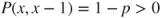 . We recall that
. We recall that 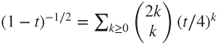 .
.
Compute
 for
for  and
and  . Compute
. Compute 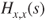 and then
and then 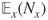 . When is this random walk recurrent?
. When is this random walk recurrent?
3.2 Symmetric random Walks with independent coordinates Let ![]() be the transition matrix of the symmetric random walk on
be the transition matrix of the symmetric random walk on ![]() , given by
, given by ![]() . Use the Potential matrix criterion to prove that
. Use the Potential matrix criterion to prove that ![]() and
and ![]() are recurrent and
are recurrent and ![]() is transient.
is transient.
3.3 Lemma 3.1.3, alternate proofs Let ![]() be a Markov chain on
be a Markov chain on ![]() with matrix
with matrix ![]() , and
, and ![]() in
in ![]() be s.t.
be s.t. ![]() is recurrent and
is recurrent and ![]() .
.
- (a) Prove that
 . Deduce from this that
. Deduce from this that  and thus that
and thus that  . Prove that
. Prove that  is recurrent, for instance using the Potential matrix criterion. Deduce from all this that
is recurrent, for instance using the Potential matrix criterion. Deduce from all this that  .
. - (b) Prove that
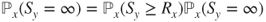 . Prove that
. Prove that 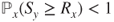 . Prove that
. Prove that  . Prove that
. Prove that  . Conclude that
. Conclude that 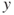 is recurrent and then that
is recurrent and then that  .
. - (c) Prove that
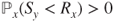 and, for
and, for 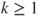 ,
,
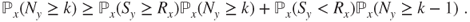
Deduce from this that
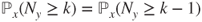 and then that
and then that  . Conclude that
. Conclude that  .
.
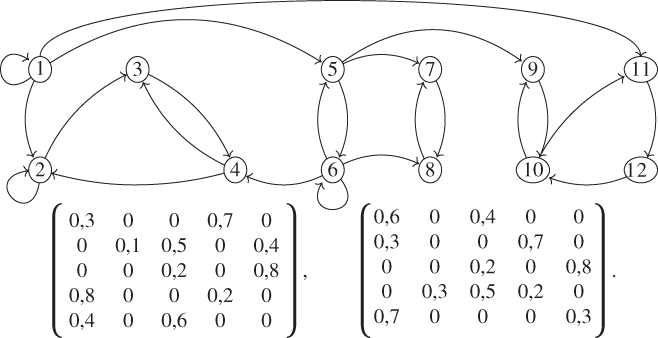
3.4 Decomposition Find the transient class and the recurrent classes for the Markov chains with graph (every arrow corresponding to a positive transition probability) and matrices given by
3.5 Genetic models, see Exercise 1.8 Decompose each state space into its transient class and its recurrent classes. Prove without computations that the population will eventually be composed of individuals having all the same allele, a phenomenon called “allele fixation.”
3.6 Balance equations on a subset Let ![]() be a transition matrix on
be a transition matrix on ![]() . Prove that for any subset
. Prove that for any subset ![]() of
of ![]() an invariant measure
an invariant measure ![]() satisfies the balance equation
satisfies the balance equation
3.7 See Lemma 3.1.1 Let ![]() be a Markov chain on
be a Markov chain on ![]() having an invariant law
having an invariant law ![]() . Prove that
. Prove that ![]() . Deduce from this that
. Deduce from this that ![]() or
or ![]() .
.
3.8 Induced chain, see Exercise 2.3 Let ![]() be an irreducible transition matrix.
be an irreducible transition matrix.
- (a) Prove that the induced transition matrix
 is recurrent if and only if
is recurrent if and only if 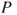 is recurrent.
is recurrent. - (b) If
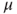 is an invariant measure for
is an invariant measure for 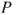 , find an invariant measure
, find an invariant measure 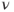 for
for 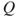 . If
. If 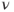 is an invariant measure for
is an invariant measure for  , find an invariant measure
, find an invariant measure 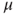 for
for 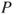 .
. - (c) Prove that if
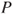 is positive recurrent, then
is positive recurrent, then 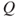 is positive recurrent.
is positive recurrent. - (d) Let
 and
and 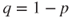 . Let
. Let  on
on 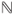 given by
given by  and
and 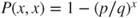 and
and 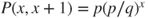 for
for  , and
, and  . Compute
. Compute  , prove that
, prove that 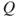 is positive recurrent and that
is positive recurrent and that  is null recurrent.
is null recurrent.
3.9 Difficult advance Let ![]() be the Markov chain on
be the Markov chain on ![]() with matrix given by
with matrix given by ![]() for
for ![]() and
and ![]() for
for ![]() , with
, with ![]() and
and ![]() .
.
- (a) Prove that
 is irreducible. Are there any reversible measures?
is irreducible. Are there any reversible measures? - (b) Find the invariant measures. Is there uniqueness for these?
- (c) Prove that the chain is recurrent positive if and only if
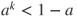 , and compute then the invariant law. What is the value of
, and compute then the invariant law. What is the value of 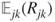 for
for 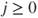 ?
? - (d) Let
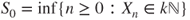 and
and 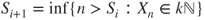 and
and  ,
, 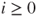 . Prove that the
. Prove that the 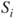 are stopping times which are finite, a.s. Prove that
are stopping times which are finite, a.s. Prove that 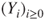 is a Markov chain on
is a Markov chain on 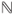 and give its transition matrix
and give its transition matrix 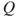 .
. - (e) Let
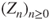 be the induced chain constituted of the successive distinct states visited by
be the induced chain constituted of the successive distinct states visited by 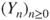 . We admit it is a Markov chain, see Exercise 2.3. Give its transition matrix
. We admit it is a Markov chain, see Exercise 2.3. Give its transition matrix 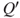 .
. - (f) Use known results to prove that
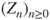 is null recurrent if
is null recurrent if 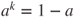 and transient if
and transient if 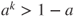 . Deduce from this that the same property for
. Deduce from this that the same property for 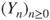 and for
and for 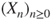 .
.
3.10 Queue with ![]() servers, 1 The evolution of a queue with
servers, 1 The evolution of a queue with ![]() servers is given by a birth-and-death chain on
servers is given by a birth-and-death chain on ![]() s.t.
s.t. ![]() and
and ![]() for
for ![]() , with
, with ![]() and
and ![]() . Let
. Let ![]() .
.
- (a) Is this chain irreducible?
- (b) Prove that there is a unique invariant measure, and compute it in terms of
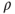 and
and  .
. - (c) Prove that the chain is positive recurrent if and only if
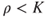 .
. - (d) Prove that the chain is null recurrent if
 and transient if
and transient if  , first using results on birth-and-death chains, and then using Lyapunov functions.
, first using results on birth-and-death chains, and then using Lyapunov functions. - (e) We now considered the generalized case in which
 , so that
, so that 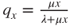 . Prove that there is an invariant law
. Prove that there is an invariant law 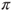 , compute it explicitly, and prove that the chain is positive recurrent. Compute
, compute it explicitly, and prove that the chain is positive recurrent. Compute 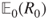 .
.
3.11 ALOHA The ALOHA protocol was established in 1970 in order to manage a star-shaped wireless network, linking a large number of computers through a central hub on two frequencies, one for sending and the other for receiving.
A signal regularly emitted by the hub allows to synchronize emissions by cutting time into timeslots of same duration, sufficient for sending a certain quantity of bits called a packet. If a single computer tries to emit during a timeslot, it is successful and the packet is retransmitted by the hub to all computers. If two or more computers attempt transmission in a timeslot, then the packets interfere and the attempt is unsuccessful; this event is called a collision. The only information available to the computers is whether there has been at least one collision or not. When there is a collision, the computers attempt to retransmit after a random duration. For a simple Markovian analysis, we assume that this happens with probability ![]() in each subsequent timeslot, so that the duration is geometric.
in each subsequent timeslot, so that the duration is geometric.
Let ![]() be the initial number of packets awaiting retransmission,
be the initial number of packets awaiting retransmission, ![]() be i.i.d., where
be i.i.d., where ![]() is the number of new transmission attempts in timeslot
is the number of new transmission attempts in timeslot ![]() , and
, and ![]() be i.i.d., where
be i.i.d., where ![]() with probability
with probability ![]() if the
if the ![]() -th packet awaiting retransmission after timeslot
-th packet awaiting retransmission after timeslot ![]() undergoes a retransmission attempt in timeslot
undergoes a retransmission attempt in timeslot ![]() , or else
, or else ![]() . All these r.v. are independent. We assume that
. All these r.v. are independent. We assume that
- (a) Prove that the number of packets awaiting retransmission after timeslot
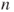 is given by
is given by
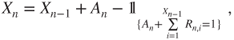
and that
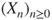 is an irreducible Markov chain on
is an irreducible Markov chain on  .
. - (b) If
 , use the Lamperti criterion (Theorem 3.3.3) to prove that this chain is transient for every
, use the Lamperti criterion (Theorem 3.3.3) to prove that this chain is transient for every  .
. - (c) Conclude to the same result when
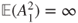 .
.
3.12 Queuing by sessions Time is discrete, ![]() jobs arrive at time
jobs arrive at time ![]() in i.i.d. manner, and
in i.i.d. manner, and ![]() and
and ![]() . Session
. Session ![]() is devoted to servicing exclusively and exhaustively the
is devoted to servicing exclusively and exhaustively the ![]() jobs that were waiting at its start, and has an integer-valued random duration
jobs that were waiting at its start, and has an integer-valued random duration ![]() , which conditional on
, which conditional on ![]() is integrable, independent of the rest, and has law not depending on
is integrable, independent of the rest, and has law not depending on ![]() .
.
- (a) Prove that
 is a Markov chain on
is a Markov chain on 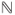 .
. - (b) Prove that
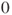 belongs to a closed irreducible class and that all states outside this class are transient.
belongs to a closed irreducible class and that all states outside this class are transient. - (c) We consider the restriction of the chain to this closed irreducible class. Prove that if
 then the chain is positive recurrent.
then the chain is positive recurrent. - (d) Prove that if
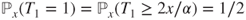 , then
, then 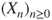 is positive recurrent. Prove that
is positive recurrent. Prove that  satisfies hypothesis
satisfies hypothesis 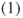 of the Lamperti criterion for
of the Lamperti criterion for 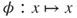 and
and 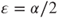 . Does it satisfy hypothesis
. Does it satisfy hypothesis 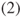 of the Lamperti criterion or of the Tweedie criterion?
of the Lamperti criterion or of the Tweedie criterion?
3.13 Big jumps Let ![]() be a Markov chain on
be a Markov chain on ![]() with matrix
with matrix ![]() with only nonzero terms
with only nonzero terms ![]() and
and ![]() .
.
- (a) Prove that this chain is irreducible.
- (b) Prove that if
 , then the chain is positive recurrent and that there exists
, then the chain is positive recurrent and that there exists 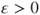 and a finite subset
and a finite subset  of
of  s.t.
s.t. 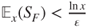 .
. - (c) Prove that if
 , then the chain is transient.
, then the chain is transient.
3.14 Quick return Let ![]() be a Markov chain on
be a Markov chain on ![]() with matrix
with matrix ![]() . Assume that there exists a nonempty subset
. Assume that there exists a nonempty subset ![]() of
of ![]() and
and ![]() and
and ![]() s.t. if
s.t. if ![]() , then
, then ![]() and
and ![]() . (We may assume that
. (We may assume that ![]() vanishes on
vanishes on ![]() .) Let
.) Let ![]() .
.
- (a) Prove that
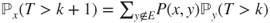 for
for  and
and 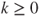 . Deduce from this that
. Deduce from this that  for
for  and
and  .
. - (b) Prove that
 and that
and that 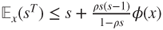 for
for  and
and 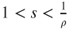 .
. - (c) Let
 , and
, and  be i.i.d., the power series
be i.i.d., the power series 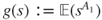 have convergence radius
have convergence radius 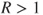 , and
, and  . Consider
. Consider  independent of
independent of  and (queue with
and (queue with  servers)
servers)
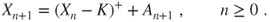
Prove that there exists
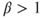 and
and  s.t.
s.t.  . Find a finite subset
. Find a finite subset  of
of  and a function
and a function 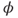 satisfying the above.
satisfying the above. - (d) Let
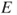 be a nonempty subset of
be a nonempty subset of 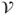 s.t.
s.t.  . Find
. Find 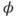 and
and 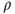 satisfying the above. For which renewal processes does this hold for
satisfying the above. For which renewal processes does this hold for 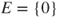 ?
?
3.15 Adjoints Let ![]() be the transition matrix of the nearest-neighbor random walk on
be the transition matrix of the nearest-neighbor random walk on ![]() , given by
, given by ![]() and
and ![]() . Give the adjoint transition matrix with respect to
. Give the adjoint transition matrix with respect to ![]() and the adjoint transition matrix with respect to the uniform measure.
and the adjoint transition matrix with respect to the uniform measure.
3.16 Labouchère system, see Exercises 1.4 and 2.10 Let ![]() be the random walk on
be the random walk on ![]() with matrix
with matrix ![]() given by
given by ![]() and
and ![]() .
.
- (a) Are there any reversible measures?
- (b) Prove that if
 , then an invariant measure must be of the form
, then an invariant measure must be of the form 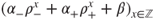 for
for 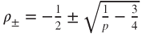 , and if
, and if  of the form
of the form 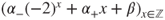 .
. - (c) By considering the behaviors for
 and
and  , prove that if
, prove that if  , then the invariant measures are of the form
, then the invariant measures are of the form 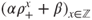 with
with 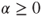 and
and  not both zero and that if
not both zero and that if  , then the unique invariant measure is uniform. Deduce from this that if
, then the unique invariant measure is uniform. Deduce from this that if 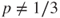 , then this random walk is transient.
, then this random walk is transient. - (d) Let
 be the random walk reflected at
be the random walk reflected at 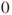 on
on  , with matrix
, with matrix 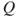 given by
given by 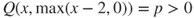 and
and  for
for  , and
, and 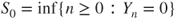 . Write the global balance equations. Prove that if
. Write the global balance equations. Prove that if  , then the unique invariant measure is
, then the unique invariant measure is 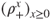 , and if
, and if 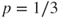 , then the unique invariant measure is uniform.
, then the unique invariant measure is uniform. - (e) Prove that
 is positive recurrent if and only if
is positive recurrent if and only if 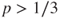 , and compute the invariant law
, and compute the invariant law 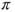 if it exists. Compute
if it exists. Compute  .
. - (f) Use a Lyapunov function technique to prove that
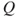 is positive recurrent if
is positive recurrent if  , null recurrent if
, null recurrent if 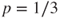 , and transient if
, and transient if 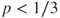 .
.
3.17 Random walk on a graph A discrete set ![]() is furnished with a (nonoriented) graph structure as follows. The elements of
is furnished with a (nonoriented) graph structure as follows. The elements of ![]() are the nodes of the graph, and the elements of
are the nodes of the graph, and the elements of ![]() are the links of the graph. The neighborhood of
are the links of the graph. The neighborhood of ![]() is given by
is given by ![]() , and the degree of
, and the degree of ![]() is given by its number of neighbors
is given by its number of neighbors ![]() . It is assumed that
. It is assumed that ![]() for every
for every ![]() . The random walk on the graph
. The random walk on the graph ![]() is defined as the Markov chain
is defined as the Markov chain ![]() on
on ![]() s.t. if
s.t. if ![]() , then
, then ![]() is chosen uniformly in
is chosen uniformly in ![]() .
.
- (a) Give an explicit expression for the transition matrix
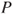 of
of  . Give a simple condition for it to be irreducible.
. Give a simple condition for it to be irreducible. - (b) Describe the symmetric nearest-neighbor random walk on
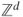 and the microscopic representation of the Ehrenfest Urn as random walks on graphs.
and the microscopic representation of the Ehrenfest Urn as random walks on graphs. - (c) Assume that
 is irreducible. Find a reversible measure for this chain. Give a simple necessary and sufficient condition for the chain to be positive recurrent and then give an expression for the invariant law
is irreducible. Find a reversible measure for this chain. Give a simple necessary and sufficient condition for the chain to be positive recurrent and then give an expression for the invariant law 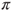 .
. - (d) Let
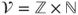 and
and
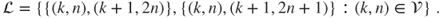
Find two (nonproportional) invariant measures for the random walk. Prove that the random walk is transient.
3.18 Caricature of TCP In a caricature of the transmission control protocol (TCP), which manages the window sizes for data transmission in the Internet, any packet is independently received with probability ![]() , and the consecutive distinct window sizes (in packets)
, and the consecutive distinct window sizes (in packets) ![]() for
for ![]() constitute a Markov chain on
constitute a Markov chain on ![]() , with matrix
, with matrix ![]() with nonzero terms
with nonzero terms ![]() and
and ![]() .
.
- (a) Prove that this Markov chain is irreducible. Prove that there exists a unique invariant law
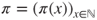 , by using a Lyapunov function technique.
, by using a Lyapunov function technique. - (b) Write the global balance equations satisfied by the invariant law
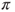 .
. - (c) Prove that, for
 ,
,
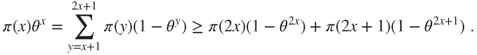
- (d) Deduce from this, for
 , that
, that 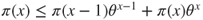 and then that
and then that  .
. - (e) Prove that
 .
. - (f) Let
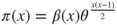 and
and  . Prove that
. Prove that 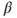 is nondecreasing,
is nondecreasing,  , and
, and 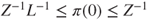 .
.
