Chapter 1
First steps
1.1 Preliminaries
This book focuses on a class of random evolutions, in discrete time (by successive steps) on a discrete state space (finite or countable, with isolated elements), which satisfy a fundamental assumption, called the Markov property. This property can be described informally as follows: the evolution “forgets” its past and is “regenerated” at each step, retaining as sole past information for its future evolution its present state. The probabilistic description of such an evolution requires
- a law (probability measure) for drawing its initial state and
- a family of laws for drawing iteratively its state at the “next future instant” given its “present state,” indexed by the state space.
Such a random evolution will be called a Markov chain.
Precise definitions can be found in the Appendix, Section A.3, but we give now the probabilistic framework. A probability space 
will be considered throughout. When 
is discrete, usually its measurable structure is given by the collection of all subsets, and all functions with values in 
are assumed to be measurable.
A random variable (r.v.) with values in a measurable state space 
is a measurable function
Intuitively, the output 
varies randomly with the input 
, which is drawn in 
according to 
, and the measurability assumptions allow to assign a probability to events defined through 
.
For the random evolutions under investigation, the natural random elements are sequences 
taking values in the same discrete state space 
, which are called (random) chains or (discrete time) processes. Each 
should be an r.v., and its law 
on the discrete space 
is then given by
and hence can be identified in a natural way with 
.
Finite-dimensional marginals
More generally, for any 
and 
in 
, the random vector
takes values in the discrete space 
, and its law 
can be identified with the collection of the
All these laws for 
and 
constitute the family of the finite-dimensional marginals of the chain 
or of its law.
Law of the chain
The r.v.
takes values in 
, which is uncountable as soon as 
contains at least two elements. Hence, its law cannot, in general, be defined by the values it takes on the elements of 
. In the Appendix, Section A.3 contains some mathematical results defining the law of 
from its finite-dimensional marginals.
Section A.1 contains some more elementary mathematical results used throughout the book, and Section A.2 a discussion on the total variation norm and on weak convergence of laws.
1.2 First properties of Markov chains
1.2.1 Markov chains, finite-dimensional marginals, and laws
1.2.1.1 First definitions
We now provide rigorous definitions.
Markov chain evolution
A family 
of laws on 
indexed by 
is defined by
The evolution of 
can be obtained by independent draws, first of 
according to 
, and then iteratively of 
according to 
for 
without taking any further notice of the evolution before the present time 
or of its actual value.
Inhomogeneous Markov chains
A more general and complex evolution can be obtained by letting the law of the steps depend on the present instant of time, that is, using the analogous formulae with 
instead of 
; this corresponds to a time-inhomogeneous Markov chain, but we will seldom consider this generalization.
Markov chain graph
The graph of the transition matrix 
, or of a Markov chain with matrix 
, is the oriented marked graph with nodes given by the elements of 
and directed links given by the ordered pairs 
of elements of 
such that 
marked by the value of 
. The restriction to the graph to 
in 
is of the form [if 
]
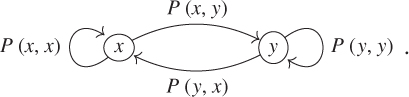
The graph and the matrix are equivalent descriptors for the random evolution. The links from 
to 
in the graph are redundant as they are marked by 
, but illustrate graphically the possible transitions from 
.
1.2.1.2 Conditional formulations
The last formula in Definition 1.2.1 can be written as
which is often used as the definition. Moreover, if 
is nonnegative or bounded then
For the sake of mathematical efficiency and simplicity, nonconditional expressions will be stressed, before possibly being translated into equivalent conditional formulations. As an example, Definition 1.2.1 immediately yields by summing over 
that
which is not quite so obvious starting from (1.2.1).
1.2.1.3 Initial law, instantaneous laws
For a Markov chain 
, the law of 
of 
is called the instantaneous law at time 
and 
the initial law. The notations 
and 
implicitly imply that 
is given and arbitrary, 
and 
for some law 
on 
indicate that 
, and 
and 
indicate that 
. By linearity,
A frequent abuse of notation is to write 
, and so on.
1.2.1.4 Law on the canonical space of the chain
The notions in the Appendix, Section A.3.4, will now be used.
Definition 1.2.1 is actually a statement on the law of the Markov chain 
, which it characterizes by giving an explicit expression for its finite-dimensional marginals in terms of its initial law 
and transition matrix 
.
Indeed, some rather simple results in measure theory show that there is uniqueness of a law on the canonical probability space 
with product 
-field having a given finite-dimensional marginal collection.
It is immediate to check that this collection is consistent [with respect to (w.r.t.) projections] and then the Kolmogorov extension theorem (Theorem A.3.10) implies that there is existence of a law 
on the canonical probability space 
with the product 
-field such that the canonical (projection) process 
has the given finite-dimensional marginal collection, which hence is a Markov chain with initial law 
and transition matrix 
(see Corollary A.3.11).
The Kolmogorov extension theorem follows from a deep and general result in measure theory, the Caratheodory extension theorem.
1.2.2 Transition matrix action and matrix notation
1.2.2.1 Nonnegative and signed measures, total variation measure, andnorm
A (nonnegative) measure 
on 
is defined by (and can be identified with) a collection 
of nonnegative real numbers and, in the sense of nonnegative series,
A measure 
is finite if its total mass 
is finite and then 
for all 
. A measure is a probability measure, or a law, if 
.
For 
in 
, let 
and 
denote the nonnegative and nonpositive parts of 
, which satisfy 
and 
.
For 
with 
, the measures 
, 
, and 
can be defined term wise. Then,
is the minimal decomposition of 
as a difference of (nonnegative) measures, which have disjoint supports, and
is called the total variation measure of 
.
If 
is such that 
is finite (equivalently, if both 
and 
are finite), then we can extend it to a signed measure 
acting on subsets of 
by setting, in the sense of absolutely converging series,
and we can define its total variation norm by
Note that 
for all 
.
The space 
of all signed measures, furnished with the total variation norm, is a Banach space, which is isomorphic to the Banach space 
of summable sequences with its natural norm.
Probability measures or laws
The space of probability measures
is the intersection of the cone of nonnegative measures with the unit sphere. It is a closed subset of 
and hence is complete for the induced metric.
Some properties of 
and 
are developed in the Appendix, Section A.2. Note that, according to the definition taken here, nonnegative measures with infinite mass are not signed measures.
Complex measures
Spectral theory naturally involves complex extensions. For its purposes, complex measures can be readily defined, and the corresponding space 
, where the modulus in 
is again denoted by 
, allows to define a total variation measure 
and total variation norm 
for 
in 
. The Banach space is isomorphic to 
. The real and imaginary parts of a complex measure are signed measures.
1.2.2.2 Line and column vectors, measure-function duality
In matrix notation, the functions 
from 
to 
are considered as column vectors 
, and nonnegative or signed measures 
on 
as line vectors 
, of infinite lengths if 
is infinite. The integral of a function 
by a measure 
is denoted by 
, in accordance with the matrix product
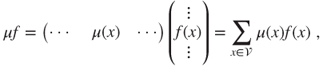
defined in 
in the sense of nonnegative series if 
and 
and in 
in the sense of absolutely converging series if 
and 
, the Banach space of bounded functions on 
with the uniform norm.
For 
subset of 
, the indicator function 
is defined by
For 
in 
, the Dirac mass at 
is the probability measure 
such that 
, that is,
For 
and 
in 
, it holds that
but 
will be represented by a line vector and 
by a column vector.
If 
is a nonnegative or signed measure, then
Duality and total variation norm
A natural duality bracket between the Banach spaces 
and 
is given by
and for 
in 
, it holds that
and hence that
Thus, 
can be identified with a closed subspace of the dual of 
with the strong dual norm, which is the norm as an operator on 
.
The space 
can be identified with the space 
of bounded sequences, and this duality between 
and 
to the natural duality between 
and 
.
The operations between complex measures and complex functions are performed by separating the real and imaginary parts.
1.2.2.3 Transition matrices, actions on measures, and functions
A matrix 
is a transition matrix if and only if each of its line vectors 
corresponds to a probability measure. Then, its column vector 
defines a nonnegative function, which is bounded by 
.
A transition matrix can be multiplied on its right by nonnegative functions and on its left by nonnegative measures, or on its right by bounded functions and on its left by signed measures. The order of these operations does not matter. The function 
, the nonnegative or signed measure 
, and 
are given for 
by
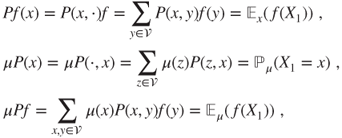
in which the notations 
and 
are used only when 
is a law.
In matrix notation,
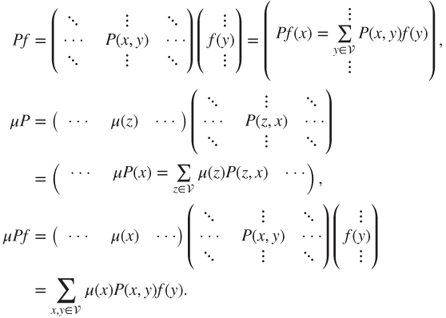
Intrinsic notation
The linear mapping
has matrix 
in the canonical basis. Its dual, or adjoint, mapping on 
, w.r.t. the duality bracket 
, is given by
and has the adjoint (or transpose) matrix, also denoted by 
. In order to respect the vector space structure and identify linear mappings and their matrices in the canonical bases, we could write 
instead of 
and 
instead of 
and 
instead of 
.
1.2.2.4 Transition matrix products, many-step transition
If 
and 
are both transition matrices on 
, then it is easy to check that the matrix product 
with generic term
is a transition matrix on 
. Let
Then,
is the probability for 
to go in one step from 
to 
, and hence for 
to do so in 
steps. In particular,
Chapman–Kolmogorov formula
As 
for 
, this yields the Chapman–Kolmogorov formula
Probabilistic interpretation
These algebraic formulae have simple probabilistic interpretations: the probability of going from 
to 
in 
steps can be obtained as the sum of the probabilities of taking every 
-step path allowing to do so, as well as the sum over all intermediate positions after 
steps.
1.2.3 Random recursion and simulation
Many Markov chains are obtained in a natural way as a random recursion, or random iterative sequence, as follows.
When a random sequence 
is defined in some particular way, there is often a natural interpretation in terms of a random recursion of the previous kind. This allows to prove that a 
is a Markov chain, without having to directly check the definition, or even having to explicit its matrix. Moreover, such a pathwise representation for the Markov chain may be used for its study or its simulation.
Any Markov chain, with arbitrary initial law 
and transition matrix 
, can be thus represented, using an i.i.d. sequence 
of uniform r.v. on 
. The state space is first enumerated as 
.
Let 
. For the initial value, if 
is determined by
then 
. For the transitions, for 
, if 
is determined by
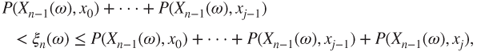
then 
.
In theory, this allows for the simulation of the Markov chain, but in practice this is not necessarily the best way to do so.
Note that this representation yields a construction for an arbitrary Markov chain, starting from a rigorous construction of i.i.d. sequences of uniform r.v. on 
, without having to use the more general Kolmogorov extension theorem (Theorem A.3.10).
1.2.4 Recursion for the instantaneous laws, invariant laws
The instantaneous laws 
satisfy the recursion
with solution 
. This is a linear recursion in dimension 
, and the affine constraint 
allows to reduce it to an affine recursion in dimension 
. Note that 
for 
.
An elementary study of this recursion starts by searching for its fixed points. These are the only possible large 
limits for the instantaneous laws, for any topology such that 
is continuous.
By definition, a fixed point for this recursion is a law (probability measure) 
such that 
, and is called an invariant law or a stationary distribution for (or of) the matrix 
, or the Markov chain 
.
Stationary chain, equilibrium
If 
is an invariant law and 
, then 
for all 
in 
, and 
is again a Markov chain with initial law 
and transition matrix 
. Then, 
is said to be stationary, or in equilibrium.
Invariant measures and laws
In order to find an invariant law, one must:
- Solve the linear equation
. - Find which solutions
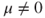are nonnegative, that is, such that 
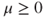. - Normalize such
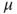by setting 
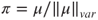, which is possible only if
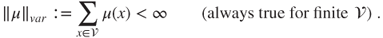
A nonnegative measure 
such that 
is called an invariant measure. An invariant measure is said to be unique if it is unique up to a multiplicative factor, that is, if all invariant measures are proportional (to it).
Algebraic interpretation
The invariant measures are the left eigenvectors for the eigenvalue 1 for the matrix 
acting on nonnegative measures, that is, for the adjoint (or transposed) matrix 
acting on nonnegative vectors. Note that the constant function 
is a right eigenvector for the eigenvalue 
, as
The possible convergence of 
to an invariant law 
is related to the moduli of the elements of the spectrum of the restriction of the action of 
on the signed measures of null total mass.
More generally, the exact or approximate computation of 
depends in a more or less explicit way on a spectral decomposition of 
.