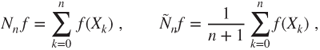Chapter 4
Long-time behavior
4.1 Path regeneration and convergence
In this section, let 
be an irreducible recurrent Markov chain on 
. For 
, let the counting measure 
with integer values, and the empirical measure 
, which is a probability measure, be the random measures given by
so that if 
is a real function on 
, then
and if 
is in 
, then
For any state 
, Lemma 3.1.3 yields that 
, and hence that the successive hitting times 
of 
defined in (2.2.2) are stopping times, which are finite, a.s. Moreover, if 
, then
As 
is the first strict future hitting time of 
by the shifted chain 
, the strong Markov property yields that the 
for 
are i.i.d. and have same law as 
when 
. In particular, for any real function 
, the
are i.i.d. and have same law as 
when 
.
The path followed by the chain can be decomposed into its excursions from 
, by setting (with the convention that an empty sum is null)
This will enable to use classic convergence results for i.i.d. sequences.
4.1.1 Pointwise ergodic theorem, extensions
4.1.1.1 Pointwise ergodic theorem
The first result is basically a strong law of large numbers and is often used for positive recurrent chains. The terminology “pointwise” refers to a.s. convergence.
Note that if 
is a transient state for a Markov chain 
, then it is visited at most a finite number of times, and 
, a.s.
Statistical estimation of transition matrix
The pointwise ergodic theorem allows to estimate the transition matrix of an irreducible positive recurrent Markov chain.
Indeed, the snake chain 
is irreducible on its natural state space
and on this space has invariant law with generic term 
, and hence, it is positive recurrent. The pointwise ergodic theorem then yields that
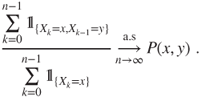
In theory, this could be also used for null recurrent chains (replacing the invariant law by the invariant measure); however, in practice, the convergence is much too slow.
4.1.1.2 Ergodic theorem in probability
Given this proof, it is natural to try to relax the assumptions and consider the case in which 
, instead of 
. The difficulty is that the last hitting time of 
before time 
, given by
with the convention 
, is not a stopping time.
The following lemma is usually proved using some results of convergence of 
, which we discuss later. We replace these by a coupling argument.
The following lemma is technical and is used to clarify statements.
In general, there is not a.s. convergence, see Chung, K.L. (1967), p. 97.
4.1.2 Central limit theorem for Markov chains
Obtaining confidence intervals is essential in practice, notably for elaborating and calibrating Monte Carlo methods (see Section 5.2) or statistical estimations. Note that 
has expectation 
. Recall (4.1.1) and (4.1.2).
Theorem 14.7 and its Corollary in Chung, K.L. (1967), p. 88 give unpractical formulae for computing 
, which can only be useful in very simple cases. Statistical or Monte Carlo methods may yield good approximations for 
. The most interesting framework is the one for the pointwise ergodic theorem, when 
and 
. If 
and 
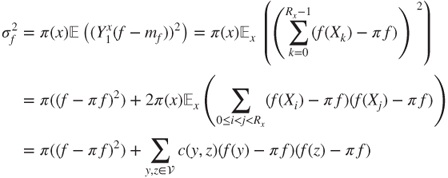
in which the coefficients 
depend on the chain evolution in a complex way. Note that 
.
It is possible to accumulate similar limit theorems using these ideas, such as an iterated logarithm law for Markov chains, see Chung, K.L. (1967), Section I.16.
4.1.3 Detailed examples
4.1.3.1 Nearest-neighbor random walks
Consider the nearest-neighbor random walk reflected at 
on 
, with matrix 
given for 
by
We have seen that it is positive recurrent if and only if 
, and we have then computed its invariant law 
. For instance, the proportion of time before time 
spent at the boundary 
is given by
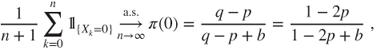
the limit being given by the pointwise ergodic theorem. We have seen that it is null recurrent for 
, and we have computed its invariant measure 
. For instance, the ratio of the time before time 
spent at 
and that spent at 
is likewise given by
4.1.3.2 Ehrenfest Urn
See Section 1.4.4. Before time 
, the proportion (or fraction) of time in which compartment 
is empty is given by
and that in which the number of molecules in compartment 
is 
by
see (3.2.6) and thereafter. State 
is hugely more frequent than state 
. Its frequency of order 
can be interpreted in terms of the central limit theorem, according to which the mass of the invariant law 
is concentrated on a scale of 
around 
. The pointwise ergodic theorem yields that
and for instance for 
and 
this yields
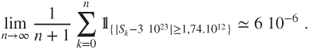
4.1.3.3 Word search
See Section 1.4.6. The invariant law 
has been computed in a specific occurrence and seen that the Markov chain is irreducible. Theorem 3.2.4 or its Corollary 3.2.7 yields that the chain is positive recurrent.
The frequency of nonoverlapping occurrences of the word GAG in the first 
characters of the infinite string is given by
Such results can be used for statistical tests to check whether the character string is indeed generated according to the model we have described.
4.2 Long-time behavior of the instantaneous laws
4.2.1 Period and aperiodic classes
4.2.1.1 Period and aperiodicity
For certain Markov chains, certain states are periodically “forbidden”: for instance, the nearest-neighbor random walk on 
, with matrix 
given by 
and 
, alternates between even and odd states and exhibits a period of 
.
If 
, then the period is not defined (it could be said that it is infinity).
Note that 
is stable by addition, as 
for 
and 
, and that the period 
is the least 
such that 
is aperiodic for the transition matrix 
. These remarks are used in the proof of the following.