Appendix A
Complements
A.1 Basic probabilistic notions
A.1.1 Discrete random variable, expectation, and generating function
A.1.1.1 General random variable and its law
A probability space ![]() will be considered throughout. In general, an r.v. with values in a measurable state space
will be considered throughout. In general, an r.v. with values in a measurable state space ![]() is a measurable function
is a measurable function
Then, for every measurable subset ![]() of
of ![]() , it holds that
, it holds that
The law of ![]() is the probability measure defined on
is the probability measure defined on ![]() by
by ![]() and, more concretely, for measurable subsets
and, more concretely, for measurable subsets ![]() , by
, by
A.1.1.2 Random variable with discrete state space
Laws and expectations
In this appendix, ![]() will be assumed to be discrete (finite or countably infinite), with measurable structure (
will be assumed to be discrete (finite or countably infinite), with measurable structure (![]() -field) given by the collection of all subsets. Then,
-field) given by the collection of all subsets. Then, ![]() is an r.v. if and only if
is an r.v. if and only if
In the sense of nonnegative or absolutely convergent series,
for ![]() and functions
and functions ![]() , which are nonnegative (and then
, which are nonnegative (and then ![]() is in
is in ![]() ) or satisfy
) or satisfy ![]() (and then
(and then ![]() is in
is in ![]() ).
).
Thus, the law ![]() of
of ![]() can be identified with the collection
can be identified with the collection ![]() of nonnegative real numbers with sum
of nonnegative real numbers with sum ![]() .
.
More generally, a (nonnegative) measure ![]() on a discrete space
on a discrete space ![]() can be identified with a collection
can be identified with a collection ![]() of nonnegative real numbers, and
of nonnegative real numbers, and
where ![]() is nonnegative or satisfies
is nonnegative or satisfies ![]() . Then,
. Then, ![]() and
and ![]() .
.
Note that the sum of a nonnegative or an absolutely converging series does not depend on the order of summation.
Integer valued random variables, possibly infinite
The natural state space of some random variables is ![]() , for instance when they are defined as an infimum of a possibly empty subset of
, for instance when they are defined as an infimum of a possibly empty subset of ![]() or as a possibly infinite sum of integers. The first step in their study is to try to determine whether
or as a possibly infinite sum of integers. The first step in their study is to try to determine whether ![]() , and if yes to compute this quantity.
, and if yes to compute this quantity.
Distribution tails
For this, the formula
is often more practical than ![]() . We give a related formula for
. We give a related formula for ![]() . Recall that if
. Recall that if ![]() , then
, then ![]() , and that
, and that
This formula is a particular instance of the following integration by parts formula: if ![]() is an
is an ![]() -valued r.v., and
-valued r.v., and ![]() is absolutely continuous and has nonnegative density
is absolutely continuous and has nonnegative density ![]() , then by the Fubini theorem
, then by the Fubini theorem
Generating functions
The generating function for (the law of) an r.v. X with values in ![]() is denoted by
is denoted by ![]() and is given by the power series
and is given by the power series
possibly extended to ![]() . If
. If ![]() , then
, then ![]() , and this formula can be used (with proper care) for
, and this formula can be used (with proper care) for ![]() with the convention
with the convention ![]() . If
. If ![]() , then
, then
and thus the convergence radius is greater than or equal to ![]() . Hence,
. Hence, ![]() is finite and continuous on
is finite and continuous on ![]() and has derivatives of all orders
and has derivatives of all orders ![]() at
at ![]() given by
given by

The function ![]() is determined by its restriction on
is determined by its restriction on ![]() , and for some computations, it is easier to work on this restriction.
, and for some computations, it is easier to work on this restriction.
Inversion formula
A Taylor series expansion of ![]() at
at ![]() shows that
shows that
which provides a theoretical inversion method yielding the law from the generating function. In practice, algebraic series expansions should be preferred.
Moments
Using the monotone convergence theorem (Theorem A.3.2), in ![]() ,
,

and the moments can be obtained from the second formula. If ![]() , then
, then ![]() and
and ![]() can be computed using the Taylor expansion of order
can be computed using the Taylor expansion of order ![]() for
for ![]() at
at ![]() , given by
, given by
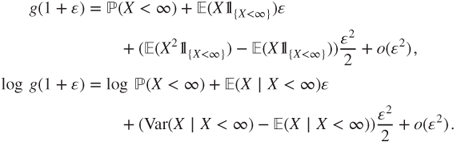
If ![]() and
and ![]() , then these Taylor expansions limited to order
, then these Taylor expansions limited to order ![]() yield
yield ![]() .
.
Sums of independent random variables
The following result is one of the reasons that generating functions are important. The converse of this result uses multivariate generating functions.
Tail distributions
The following result is an application of the ideas of Lemma A.1.1 to generating functions.
A.1.2 Conditional probabilities and independence
A.1.2.1 Conditioning and total probability formula
If ![]() and
and ![]() are two events,
are two events, ![]() can be denoted in some circumstances by
can be denoted in some circumstances by ![]() , and it is said “
, and it is said “![]() and
and ![]() .”
.”
If ![]() , then we define the probability of
, then we define the probability of ![]() conditional on
conditional on ![]() by
by
and ![]() is a probability measure on
is a probability measure on ![]() .
.
If ![]() is a nonnegative or integrable r.v. for
is a nonnegative or integrable r.v. for ![]() , then its expectation or variance conditional to
, then its expectation or variance conditional to ![]() s.t.
s.t. ![]() is defined as its expectation or variance for
is defined as its expectation or variance for ![]() , that is,
, that is,
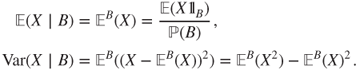
Iterated conditioning
If ![]() is an event s.t.
is an event s.t. ![]() , or equivalently
, or equivalently ![]() , then
, then
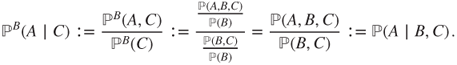
Total probability
If ![]() is a countable collection of events s.t.
is a countable collection of events s.t.
then the probability of any event ![]() or the expectation of any nonnegative or integrable r.v.
or the expectation of any nonnegative or integrable r.v. ![]() can be obtained as
can be obtained as

with the natural convention ![]() for
for ![]() .
.
A.1.2.2 Independence and conditional independence
Independent events
Two events ![]() and
and ![]() are independent if and only if
are independent if and only if
and if ![]() this is equivalent to
this is equivalent to ![]() . For an arbitrary index set
. For an arbitrary index set ![]() , the events
, the events ![]() are independent if and only if
are independent if and only if
Independent random variables, i.i.d. family
Two random variables ![]() and
and ![]() are independent if and only if, for all measurable
are independent if and only if, for all measurable ![]() and
and ![]() in the respective state spaces,
in the respective state spaces, ![]() and
and ![]() are independent, that is,
are independent, that is,
This expresses that the joint law ![]() is the product law
is the product law ![]() . Hence, the Fubini theorem yields that
. Hence, the Fubini theorem yields that ![]() and
and ![]() are independent if and only if, for any
are independent if and only if, for any ![]() and
and ![]() , which are nonnegative or satisfy that
, which are nonnegative or satisfy that ![]() be
be ![]() ,
,
If ![]() and
and ![]() have discrete state spaces, it is sufficient that
have discrete state spaces, it is sufficient that ![]() for every
for every ![]() and
and ![]() in the respective state spaces.
in the respective state spaces.
For an arbitrary index set ![]() , the random variables
, the random variables ![]() are independent if and only if for any
are independent if and only if for any ![]() and
and ![]() and measurable
and measurable ![]() included in the respective state spaces
included in the respective state spaces
that is, if and only if the joint laws are given by the product of the marginals
and the Fubini theorem can be used as earlier. If ![]() is finite, then it suffices to check this property for
is finite, then it suffices to check this property for ![]() .
.
The random variables ![]() are independent and identically distributed, i.i.d. for short, if they are independent and all have same law.
are independent and identically distributed, i.i.d. for short, if they are independent and all have same law.
Independent  -fields
-fields
The most general independence notion is as follows. The sub-![]() -fields
-fields ![]() of
of ![]() (see Section A.3) are independent if and only if, for all
(see Section A.3) are independent if and only if, for all ![]() and
and ![]() and
and ![]() , it holds that
, it holds that
If ![]() is finite, then it suffices to check this property for
is finite, then it suffices to check this property for ![]() .
.
Note that the random variables ![]() are independent if and only if the generated sub-
are independent if and only if the generated sub-![]() -fields
-fields ![]() are independent and that the events
are independent and that the events ![]() are independent if and only if the random variables
are independent if and only if the random variables ![]() are independent.
are independent.
Conditional independence
If ![]() is an event s.t.
is an event s.t. ![]() , all these independence notions can be applied to the conditional probability measure
, all these independence notions can be applied to the conditional probability measure ![]() , and the terminology “independent conditional to
, and the terminology “independent conditional to ![]() ” is then used. In particular,
” is then used. In particular, ![]() and
and ![]() are independent conditional to
are independent conditional to ![]() if and only if
if and only if
or, equivalently,
A.1.2.3 Basic limit theorems for i.i.d. random variables
The notion of a Markov chain is a generalization of the notion of a sequence of i.i.d. random variables. We recall two basic limit theorems for the latter. The first result shows that in a certain scale randomness tends to disappear, and the second quantifies precisely the residual randomness in the appropriate scale.
These two results have been adapted to recurrent Markov chains using regenerative techniques in Section 4.1. This has yielded notably the pointwise ergodic theorem and the Markov chain central limit theorem.
A.2 Discrete measure convergence
A.2.1 Total variation norm and maximal coupling
A.2.1.1 Total variation norm and duality
The state space ![]() will here be discrete, and we develop the notions in Section 1.2.2, see Section A.3.2 for some extensions to general measurable state spaces.
will here be discrete, and we develop the notions in Section 1.2.2, see Section A.3.2 for some extensions to general measurable state spaces.
The space ![]() of signed measures with the total variation norm can be identified to the separable (with dense countable subset) Banach space (complete normed space)
of signed measures with the total variation norm can be identified to the separable (with dense countable subset) Banach space (complete normed space) ![]() of summable real sequences indexed by
of summable real sequences indexed by ![]() with its natural norm. Its dual space
with its natural norm. Its dual space ![]() of bounded functions with the supremum norm can be identified with the space
of bounded functions with the supremum norm can be identified with the space ![]() of bounded sequences.
of bounded sequences.
These vector spaces are of finite dimension if and only if ![]() is finite. Recall that a vector space is of finite dimensions if and only if all norms are equivalent.
is finite. Recall that a vector space is of finite dimensions if and only if all norms are equivalent.
The subset ![]() of finite nonnegative measures is a closed (for the norm) cone (stable by nonnegative linear combinations) of
of finite nonnegative measures is a closed (for the norm) cone (stable by nonnegative linear combinations) of ![]() . The set
. The set ![]() of probability measures is the intersection of
of probability measures is the intersection of ![]() with the unit sphere. Thus,
with the unit sphere. Thus, ![]() is a closed convex subset of
is a closed convex subset of ![]() and is complete for the distance induced by the norm.
and is complete for the distance induced by the norm.
A.2.1.2 Total variation norm and maximal coupling
A.2.2 Duality between measures and functions
A.2.2.1 Dual Banach space and strong dual norm
Let ![]() be a Banach space. Its dual
be a Banach space. Its dual ![]() is the space of all continuous (for the norm) linear forms (real linear mappings) on
is the space of all continuous (for the norm) linear forms (real linear mappings) on ![]() . The action of
. The action of ![]() in
in ![]() on
on ![]() is denoted by duality brackets as
is denoted by duality brackets as
The strong dual norm on ![]() is given by the operator norm
is given by the operator norm
and for this norm ![]() is a Banach space.
is a Banach space.
A.2.2.2 Discrete signed measures and classic sequence spaces
Let ![]() be a discrete state space. For
be a discrete state space. For ![]() , let
, let ![]() and
and ![]() denote the spaces of real sequences
denote the spaces of real sequences ![]() s.t., respectively,
s.t., respectively,
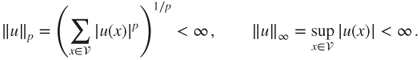
If ![]() is finite, then all these finite sequence spaces can be identified to elements of
is finite, then all these finite sequence spaces can be identified to elements of ![]() , and all these norms are equivalent. The main focus is on infinite
, and all these norms are equivalent. The main focus is on infinite ![]() , and these spaces are isomorphic to the classic spaces of sequences indexed by
, and these spaces are isomorphic to the classic spaces of sequences indexed by ![]() .
.
The Banach space ![]() of signed measures on
of signed measures on ![]() with the total variation norm can be identified with the separable space
with the total variation norm can be identified with the separable space ![]() , and its dual
, and its dual ![]() with
with ![]() by identifying
by identifying ![]() in
in ![]() with the linear form
with the linear form
and the norms are in duality with this duality bracket.
The Banach space ![]() is the subspace of
is the subspace of ![]() of the sequences that converge to
of the sequences that converge to ![]() : for all
: for all ![]() , there exists a finite subset
, there exists a finite subset ![]() of
of ![]() s.t.
s.t. ![]() for
for ![]() in
in ![]() . Then, with continuous injections,
. Then, with continuous injections,
The countable space of sequences with finite support is dense in ![]() and in
and in ![]() for
for ![]() , and these Banach spaces hence are separable.
, and these Banach spaces hence are separable.
On the contrary, ![]() is not separable for in finite
is not separable for in finite ![]() , and its dual contains strictly
, and its dual contains strictly ![]() . Indeed, let
. Indeed, let ![]() be a sequence with values in
be a sequence with values in ![]() ,
, ![]() an enumeration of
an enumeration of ![]() , and
, and ![]() if
if ![]() and else
and else ![]() . Then,
. Then, ![]() is in
is in ![]() and
and
and thus ![]() cannot be dense in
cannot be dense in ![]() .
.
The dual space of ![]() can be identified with
can be identified with ![]() , with duality bracket for
, with duality bracket for ![]() in
in ![]() and
and ![]() in
in ![]() again given by
again given by
For ![]() in
in ![]() , for all
, for all ![]() , there exists a finite subset
, there exists a finite subset ![]() of
of ![]() s.t.
s.t. ![]() , which readily yields using Lemma A.2.1 that
, which readily yields using Lemma A.2.1 that
so that the total variation norm (or the ![]() norm) is the strong dual norm both considering
norm) is the strong dual norm both considering ![]() (or
(or ![]() ) as the dual of
) as the dual of ![]() or as a subspace of the dual of
or as a subspace of the dual of ![]() .
.
A.2.2.3 Weak topologies
The Banach space ![]() can be given the weak topology
can be given the weak topology
also denoted by ![]() . It can also be considered as the dual space of
. It can also be considered as the dual space of ![]() , and given the weak-
, and given the weak-![]() topology
topology
also denoted by ![]() . Recall that in infinite dimension the dual space of
. Recall that in infinite dimension the dual space of ![]() is much larger than
is much larger than ![]() .
.
A simple fact is that a sequence ![]() converges for
converges for ![]() if and only if it is bounded (for the norm) and converges termwise. A diagonal subsequence extraction procedure then shows that a subset of
if and only if it is bounded (for the norm) and converges termwise. A diagonal subsequence extraction procedure then shows that a subset of ![]() is relatively compact for
is relatively compact for ![]() if and only if it is bounded.
if and only if it is bounded.
Let ![]() be infinite and identified with
be infinite and identified with ![]() . Then, the sequence
. Then, the sequence ![]() of
of ![]() clearly converges to
clearly converges to ![]() for
for ![]() , and hence
, and hence ![]() is not closed for this topology. Moreover, this sequence cannot have an accumulation point for
is not closed for this topology. Moreover, this sequence cannot have an accumulation point for ![]() , as this could only be
, as this could only be ![]() as per the above-mentioned conditions, whereas
as per the above-mentioned conditions, whereas ![]() . Hence, the bounded set
. Hence, the bounded set ![]() is not relatively compact for
is not relatively compact for ![]() nor for the (stronger) topology of the total variation norm.
nor for the (stronger) topology of the total variation norm.
These are instances of far more general facts. Recall that a normed vector space is of finite dimension if and only if its unit sphere is compact and that the unit sphere is always compact for the weak-![]() topology (but not necessarily for the weak topology), which helps explain its popularity, see the Banach–Alaoglu theorem (Rudin, W. (1991), Theorem 3.15).
topology (but not necessarily for the weak topology), which helps explain its popularity, see the Banach–Alaoglu theorem (Rudin, W. (1991), Theorem 3.15).
A.2.3 Weak convergence of laws and convergence in law
Let us now assume that the above-mentioned notions are restricted to the space of probability measures ![]() , that is, that both the sequence
, that is, that both the sequence ![]() and its limit
and its limit ![]() are probability measures.
are probability measures.
Then, not only the ![]() and
and ![]() topologies coincide (a fact which extends to general state spaces), but as
topologies coincide (a fact which extends to general state spaces), but as ![]() is discrete, they also coincide with both the topology of the termwise convergence (product topology) and the topology of the complete metric space given by the (trace of the) total variation norm.
is discrete, they also coincide with both the topology of the termwise convergence (product topology) and the topology of the complete metric space given by the (trace of the) total variation norm.
The resulting topology is called the topology of weak convergence of probability measures. The convergence in law of random variables is defined as the weak convergence of their laws.
Indeed, clearly on ![]() , the weakest topology is that of termwise convergence, and the strongest is that of total variation. Let
, the weakest topology is that of termwise convergence, and the strongest is that of total variation. Let ![]() for
for ![]() and
and ![]() be in
be in ![]() , and
, and ![]() for every
for every ![]() in
in ![]() . Let
. Let ![]() be arbitrary. It is possible to choose a finite subset
be arbitrary. It is possible to choose a finite subset ![]() of
of ![]() and then
and then ![]() s.t.
s.t.
As these are probability measures, if ![]() , then
, then
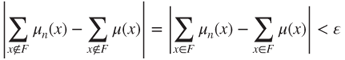
and thus, ![]() , and hence,
, and hence,
A.2.3.1 Relative compactness and tightness
The fact that ![]() is weak-
is weak-![]() relatively compact in
relatively compact in ![]() , and computations quite similar to that shown earlier, show that a subset
, and computations quite similar to that shown earlier, show that a subset ![]() of
of ![]() is relatively compact for the weak convergence of probability measures if and only if
is relatively compact for the weak convergence of probability measures if and only if ![]() is tight, in the following sense: for every
is tight, in the following sense: for every ![]() , there exists a finite subset
, there exists a finite subset ![]() of
of ![]() s.t.
s.t.
