Chapter 2
Past, present, and future
2.1 Markov property and its extensions
2.1.1 Past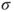 
-field, filtration, and translation operators
Let 
be a sequence of random variables. The 
-fields
contain all events that can be observed using exclusively 
, that is, the past up to time 
included of the sequence. Obviously
A family of nondecreasing 
-fields, such as 
, is called a filtration, and provides a mathematical framework for the accumulation of information obtained by the step-by-step observation of the sequence.
Product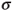 
-field
Definition 1.2.1 gives an expression for the probability of any event 
in 
in terms of 
and 
. The Kolmogorov extension theorem (Theorem A.3.10) in Section A.3.4 of the Appendix then attributes a corresponding probability to any event in the product 
-field of 
, which is the smallest 
-field containing every 
, which we denote by 
. The 
-field 
contains all the information that can be reconstructed from the observation of an arbitrarily large finite number of terms of the sequence 
.
As a 
-field is stable under countable intersections, 
contains events allowing to characterize a.s. convergences, of which we will discuss later.
Shift operators
For 
, the shift operators 
act on sequences of r.v. by
This action extends naturally to any 
-measurable random variable 
and to any event 
in 
: if 
and 
for some measurable (deterministic) function 
on 
and measurable subset 
, then
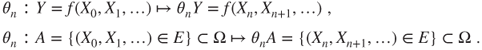
The 
-field 
is included in 
and contains the events of the future after time 
included for the sequence. It corresponds for 
to what 
corresponds for 
.
2.1.2 Markov property
Definition 1.2.1 is in fact equivalent to the following Markov property, which is apparently stronger as it yields that the past and the future of a Markov chain are independent conditional on its present state.
Thus, conditional to 
, the future after time 
of the chain is given by a “regeneration” of the chain starting at 
and independent of the past. Note that past and future are taken in wide sense and include the present: both 
and 
may contain information on 
“superseded” by the conditioning on 
. All this is illustrated by Figure 2.1, for 
.
Figure 2.1 Strong Markov property. The successive states of 
are represented by the filled circles and are linearly interpolated by dashed lines and 
is a stopping time.
These formulae are compact, have rich interpretations, and can readily be extended, for instance, if 
and 
are nonnegative or bounded then
We now proceed to further extend them by replacing deterministic instants 
by an adequate class of random instants.
2.1.3 Stopping times and strong Markov property
A stopping time will be defined as a random instant that can be determined “in real time” from the observation of the chain, and hence at which a decision (such as stopping a game) can be taken without further knowledge of the future.
The equivalences in the definition follow readily from
We set 
and 
on 
. On 
, it holds that, for 
,
For 
, it holds that 
, and for any 
, one can determine whether a certain 
is in 
by examining only 
.
Trivial example: deterministic times
If 
is deterministic, that is, if
then 
is a stopping time and 
.
We shall give nontrivial examples of stopping times after the next fundamental result, illustrated in Figure 2.1, which yields that Theorem 2.1.1 and its corollaries, such as (2.1.1), hold conditionally on 
by replacing 
with a stopping time 
.
A “last hitting time,” a “time of maximum,” and so on are generally not stopping times, as the future knowledge they imply usually prevents the formula for the strong Markov property to hold.
2.2 Hitting times and distribution
2.2.1 Hitting times, induced chain, and hitting distribution
2.2.1.1 First hitting time and first strict future hitting time
Let 
be a subset of 
. The r.v., with values in 
, defined by
are stopping times, as 
and 
. Clearly,
When 
, the notations 
and 
are used. The notations 
and 
or 
and 
, or even 
and 
if the contest is clear, will also be used. See Figure 2.2 in which 
.
Figure 2.2 Successive hitting times of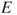 
and induced chain. The successive states of 
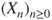are represented by the filled circles and are linearly interpolated, and 
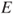corresponds to the points between the two horizontal lines. We see 
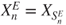for 
, 
, and 
.
Classically, 
is called the (first) hitting time of 
by the chain and 
the (first) strict future hitting time of 
by the chain.
2.2.1.2 Successive hitting times and induced chain
The successive hitting times 
of 
by the chain 
are given by
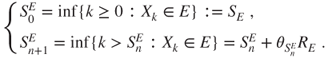
These are stopping times, as 
.
If 
then we set 
, which is the state occupied at the 
th hit of 
by the chain. This is illustrated in Figure 2.2.
If 
for every 
, then 
is said to be recurrent. Then, the strong Markov property (Theorem 2.1.3) yields that if 
, for instance, if 
a.s., then 
for all 
, and moreover that 
is a Markov chain on 
, which is called the induced chain of 
in 
.
Cemetery state
In order to define 
in all generality, we can set 
if 
for a cemetery state 
adjoined to 
. The strong Markov property implies that 
thus defined is a Markov chain on the enlarged state space 
, also called the induced chain; one can add that it is killed after its last hit of 
.
2.2.1.3 Hitting distribution and induced chain
For 
, the matrix and function
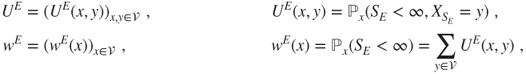
only depend on 
and on 
as the starting states are specified. When 
, the notations 
and 
are used, and 
and 
when the context is clear.
Clearly, 
for 
and 
is sub-Markovian (nonnegative terms, sum of each line bounded by 
) and is Markovian if and only if 
.
The restriction of 
to 
is Markovian if and only if 
is recurrent and then it is the transition matrix of the induced chain 
. Else, a Markovian extension of 
is obtained using a cemetery state 
adjoined to 
, and setting 
for 
in 
and 
; its restriction to 
is the transition matrix of the induced chain on the extended state space. The matrix of the chain conditioned to return to 
is given by 
.
The matrix notation conventions in Section 1.2.2 are used for 
. For 
in 
, the line vector 
is a subprobability measure, with support 
and total mass 
, called the (possibly defective) hitting distribution of 
starting from 
. It associates to 
the quantity
For 
or 
, the function 
is given for 
by
and this can be extended to signed bounded functions, by setting
Clearly, 
and 
and 
. If 
then 
and in particular 
and 
.
2.2.2 “One step forward” method, Dirichlet problem
2.2.2.1 General principle
Let 
be a Markov chain with matrix 
. The Markov property (Theorem 2.1.1) yields that the shifted chain by one step
is also a Markov chain with matrix 
and that conditional on 
it is started at 
and independent of 
. This is illustrated in Figure 2.1, with 
.
The “one step forward” method
The “one step forward” method, or the method of conditioning on the first step, exploits this fact. It consists in rewriting quantities of interest for 
in terms of the shifted chain 
and then using the above observation to establish equations for these quantities. These equations can then be solved or studied qualitatively and quantitatively.
A natural framework for this method is the study of hitting times and locations of 
, as:
- the hitting time
is a function of 
, and 
the same function of 
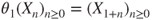; - if
then 
and 
and if 
then 
and 
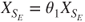on 
.
2.2.2.2 Hitting distribution and Dirichlet problem
This method will provide an equation for 
, which we are going to study.
All that matters about 
is its restriction to the boundary of 
for 
given by
and the solution is the null extension of 
.
The r.v. 
and subprobability measure 
are also called the exit time and distribution of 
by the chain, and one must take care about notation.
Dirichlet problem and recurrence
A direct consequence of Theorem 2.2.2 is that an irreducible Markov chain on a finite state space hits every state 
starting from any state 
, a.s., as irreducibility implies that 
for all 
and hence that 
, and the theorem yields that 
. The strong Markov property implies that if 
for all 
, then the Markov chain visits every state infinitely often, a.s.
We give a more general result. A subset 
of 
communicates with another subset 
of 
if for every 
there exists 
and 
such that 
. This is always the case if 
is irreducible and 
is nonempty.
2.2.2.3 Generating functions, joint distribution of hitting time, and location
Let 
be nonempty. In order to study the (defective) joint distribution of 
and 
, consider for 
, and 
the generating functions given for 
by
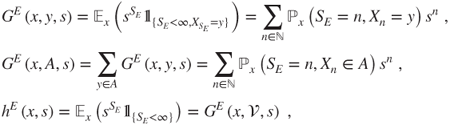
which depend only on the matrix 
of the chain. Clearly,
The notations 
and 
are used for 
, and 
and 
when the context is clear. Then
which allows to study the condition law of 
given 
and 
.
2.2.2.4 Direct computations for expectations
For 
and 
, we have
Nevertheless, it may be best to work directly on 
and 
, and possibly one may be able to solve the corresponding equations and not those for 
. Let
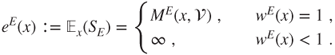
The notations 
and 
are used for 
, and 
and 
if the context is clear.
The “right-hand side” 
or 
of the affine equation is a solution of the associated linear equation, which corresponds to the Dirichlet problem (2.2.5). This fact can be exploited to find a particular solution of the affine equation.
2.3 Detailed examples
The results in this section will be now applied to some quantities of interest for the detailed examples described in Section 1.4. The main idea will be to solve the equations derived by the “one step forward” method, using the results obtained on the Dirichlet problem and related equations when appropriate.
The description of the Monte Carlo method for the approximate solution of the Dirichlet problem is left for Section 5.1.
2.3.1 Gambler's ruin
See Section 1.4.2. Here 
and 
, and the game duration is 
. We set 
. Gambler A is ruined if 
and then Gambler B wins. There is a symmetry between the gamblers by interchanging 
with 
and 
with 
.
2.3.1.1 Finite game and ruin probability
Starting from an initial fortune of 
, the probability of eventual ruin and eventual win of Gambler A are given by
and the probability that the game eventually terminates by
Proposition 2.2.4 implies that 
, but a direct proof will be provided.
Theorem 2.2.2 (or a direct implementation of the “one step forward” method) yields that 
and 
and 
are solutions of
with respective boundary conditions 
and 
, 
and 
, and 
.
This is a linear second-order recursion, with characteristic polynomial
with roots 
and 
, which can possibly be equal.
Biased game
This is the case 
, in which the roots are distinct. The general solution is given by 
, hence 
and
Fair game
This is the case 
, in which 
is a double root. The general solution is given by 
, hence 
and
These are the limits for 
going to 
of the values for the biased game.
2.3.1.2 Mean game duration
Theorem 2.2.6 yields that the function 
for 
satisfies
with 
and that 
satisfies the same equation in which 
is replaced by 
.
The general solution of such an affine equation is given by the sum of a particular solution and of the general solution to the related linear equation (2.3.7), the latter being already known. The r.h.s. 
is one of these general solutions, a fact to be exploited in order to find a particular solution.
Biased game
A particular solution of the form 
satisfies
which yields for the r.h.s. 
that 
and 
, for 
that 
, and for 
that 
and 
, the sum of the previous quantities. The null boundary conditions allow to conclude that
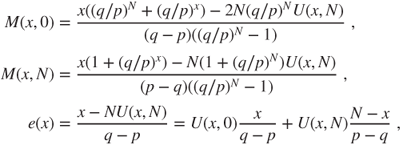
as soon as we have eliminated the possibility of infinite solutions. This is a delicate point in Theorem 2.2.6, see the remark thereafter.
As 
is finite, Proposition 2.2.4 allows to conclude. A more direct proof is that the solution for the r.h.s. 
(the formula for 
) is nondecreasing from the value 
at state 
to a certain state, then is nonincreasing down to the value 
at state 
, and hence is nonnegative, and the minimality result in Theorem 2.2.6 allows to eliminate the infinite solution.
It can be noted that 
is the mean, weighted by the probabilities of ruin and of win, of two quantities of opposite signs, which essentially correspond to a motion with speed 
. This is called a ballistic phenomenon.
Fair game
A particular solution of the form 
satisfies
which yields for 
that 
and 
, for 
that 
and 
, and for 
that 
and 
(the sums). The null boundary conditions allow to conclude that
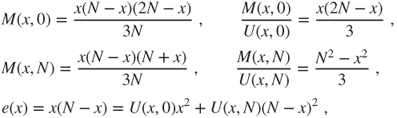
where the infinite solution can be eliminated by Proposition 2.2.4 or remarking that these solutions are nonnegative.
The mean time taken to reach a distance 
is of order 
, which corresponds to a diffusive phenomenon.