Solutions for Chapter 2
- 2.1 Then,
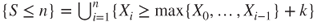 ,
,  , and
, and  .
.
- 2.2.a By definition of stopping times,
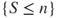 and
and 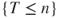 belong to
belong to  . Thus, by definition of the
. Thus, by definition of the  -field
-field  ,
,

- also belong to
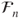 , and
, and 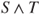 and
and 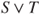 are also stopping times. Moreover,
are also stopping times. Moreover,

- where
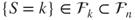 , and
, and 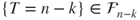 can be written as
can be written as 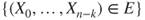 so that
so that 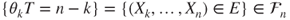 . Hence,
. Hence, 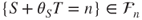 , and thus,
, and thus, 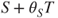 is a stopping time.
is a stopping time.
- 2.2.b If
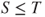 and
and 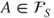 , then
, then
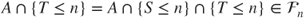
- and hence
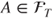 . Applying this to
. Applying this to  and
and  yields that
yields that 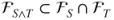 . If
. If 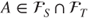 , then
, then
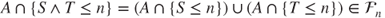
- and hence,
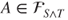 . Thus,
. Thus, 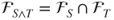 .
.
- 2.2.c Then,
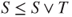 and
and  and thus,
and thus, 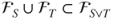 , which is a
, which is a  -field, and thus,
-field, and thus,  . Conversely, let
. Conversely, let 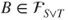 . Then,
. Then,
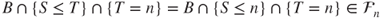
- and thus,
 , and similarly
, and similarly 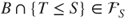 , hence
, hence
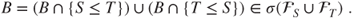
- We conclude that
 .
.
- 2.3.a The matrix
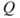 is Markovian as
is Markovian as

- Moreover,
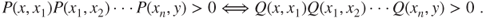
- 2.3.b As
 , the
, the  are stopping times. Moreover,
are stopping times. Moreover,
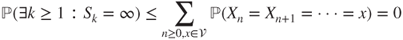
- as

- 2.3.c Let
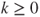 ,
, 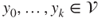 , and
, and 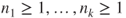 . If
. If  ,
, 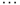 ,
,  , then
, then

or else the first and last terms in the previous equation are b03 zero and hence equal. Thus,
 is a Markov chain with the said transition matrix.
is a Markov chain with the said transition matrix.Summation over
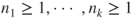 yields that
yields that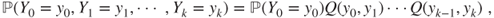
and thus,
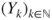 is a Markov chain with matrix
is a Markov chain with matrix 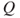 . The Markov property yields that
. The Markov property yields that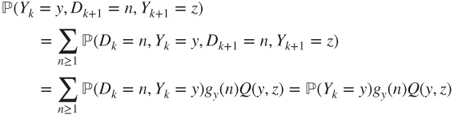
and hence,
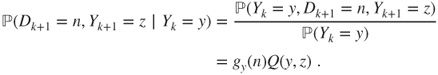
Thus,

- 2.3.d Then,
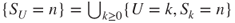 . By definition of filtrations,
. By definition of filtrations,  can be written as
can be written as 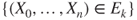 and
and  as
as  . If
. If 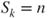 , then
, then  can be written in terms of
can be written in terms of  , i.e. that is, there exists a deterministic function
, i.e. that is, there exists a deterministic function 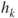 such that
such that  . Hence,
. Hence,
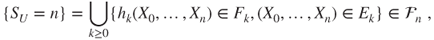
- so that
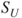 is a stopping time for
is a stopping time for 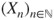 .
.
- 2.4.a Then,
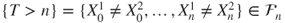 . Actually,
. Actually,  is the first hitting time of the diagonal
is the first hitting time of the diagonal 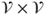 by
by 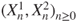 .
.
- 2.4.b Then,
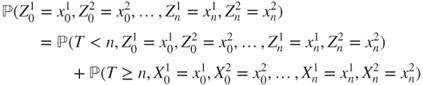
and the first r.h.s. term can be expressed as the sum over
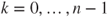 of
of
and the fact that
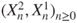 also has matrix
also has matrix 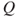 ,
,  , and the Markov property (Theorem 2.1.1) yields that this expression can be written as
, and the Markov property (Theorem 2.1.1) yields that this expression can be written as
By summing all these terms, we find that

and hence,
 has same law as
has same law as 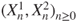 .
.Thus,

- 2.4.c All this is straightforward to check.
- 2.4.d For
 , it holds that
, it holds that  , and the Markov property (Theorem 2.1.1) yields that
, and the Markov property (Theorem 2.1.1) yields that

- and we conclude by iteration, considering that
 .
.
- 2.4.e By assumption,

- and we conclude by summing over
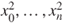 and then over
and then over 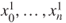 .
.
- 2.4.f As
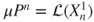 and
and 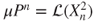 , we conclude by the previous results.
, we conclude by the previous results.
- 2.5.a Let
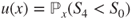 . We are interested in
. We are interested in 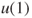 .
.
By symmetry,
 , and the “one step forward” method (Theorem 2.2.2) yields that
, and the “one step forward” method (Theorem 2.2.2) yields that 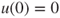 and
and  and
and  and
and 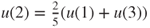 and
and 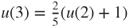 . Hence,
. Hence,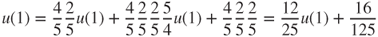
and thus
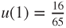 .
. - 2.5.b The visit consists in reaching module
 from module
from module  by one side, go
by one side, go  times back and forth from module
times back and forth from module  to module
to module 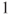 on that side, then either go to module
on that side, then either go to module 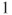 by the other side or go to module
by the other side or go to module  by the same side, and then reach module
by the same side, and then reach module 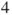 from module
from module 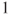 by the other side, all this without visiting module
by the other side, all this without visiting module  .
.
The Markov property (Theorem 2.1.3) and symmetry arguments yield that the probability of this event is
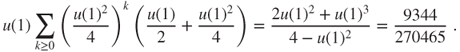
- 2.5.c Let
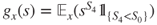 for
for 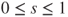 . We are interested in
. We are interested in 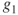 .
.
By symmetry,
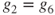 , and the “one step forward” method (Theorem 2.2.5) yields that
, and the “one step forward” method (Theorem 2.2.5) yields that  and
and 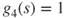 ,
, 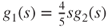 , and
, and 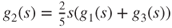 , and
, and  . Hence,
. Hence,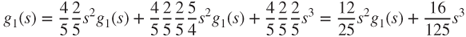
so that
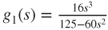 .
.We again find that
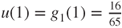 , and by identification
, and by identification
Moreover,
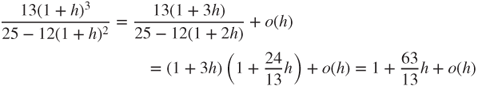
and hence,
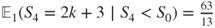 by identification.
by identification. - 2.6 We are interested in
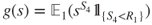 for
for  and
and 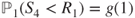 . Let
. Let 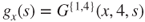 .
.
Then,
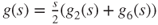 by the “one step forward” method.
by the “one step forward” method.This method also yields that (Theorem 2.2.5)
 and
and 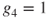 ,
, 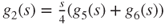 ,
, 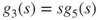 ,
, 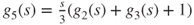 ,
, 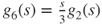 . Thus,
. Thus, 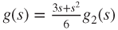 and
and  and then,
and then,
and hence,
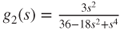 , and finally,
, and finally,
Then,
 , the conditional generating function is given by
, the conditional generating function is given by  , and a Taylor expansion at
, and a Taylor expansion at 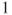 yields
yields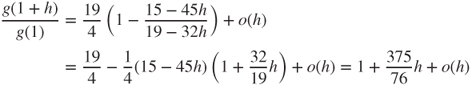
and thus, by identification, the conditional expectation is
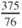 .
. - 2.7 If
 for
for  , then
, then 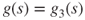 . The “one step forward” method (Theorem 2.2.5) yields that
. The “one step forward” method (Theorem 2.2.5) yields that  and
and
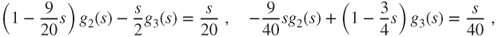
- so that

- By identification,
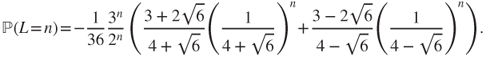
- Moreover, the Taylor expansion
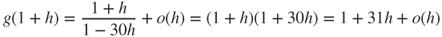
- yields that
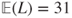 .
.
- 2.8.a This equation writes, for
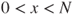 ,
,
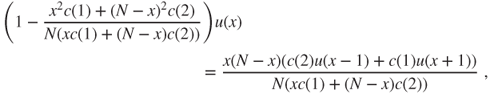
- is of the form
 and has
and has 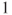 as a solution, hence the result. (The direct computation is simple.)
as a solution, hence the result. (The direct computation is simple.)
- 2.8.b This is the same equation found in the Dirichlet problem in gambler's ruin when the gain probability at each toss for Gambler A is
 (see Section 2.3.1). We refer to that section for the computation of
(see Section 2.3.1). We refer to that section for the computation of 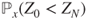 and
and  .
.
- 2.8.c Transitions are according to a binomial law. The equation is, for
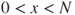 ,
,
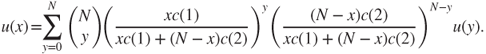
- If
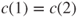 , then
, then 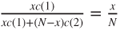 and classically (total mass and expectation of a binomial law) for
and classically (total mass and expectation of a binomial law) for 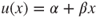 , the r.h.s. of the equation takes the value
, the r.h.s. of the equation takes the value  , and hence, as for gambler's ruin,
, and hence, as for gambler's ruin,  and
and 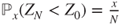 .
.
- 2.9.a The graph can be found in Section 3.1.3. Clearly,
 is irreducible.
is irreducible.
- 2.9.b If
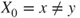 , then
, then  . For
. For  , a simple spatial translation allows to use the results in Section 2.3.2. For
, a simple spatial translation allows to use the results in Section 2.3.2. For 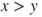 , it suffices to interchange
, it suffices to interchange 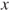 and
and 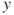 as well as
as well as  and
and 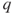 and use the previous result.
and use the previous result.
- 2.9.c By the “one step forward” method,
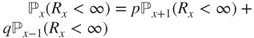 and
and  . Hence, the results follow from the previous ones.
. Hence, the results follow from the previous ones.
- 2.9.d The strong Markov property (Theorem 2.1.3) and the preceding results allow to compute
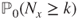 . Moreover,
. Moreover, 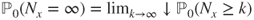 .
.
- 2.9.e If
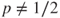 , then
, then 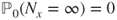 for all
for all  and the chain goes to infinity, a.s. More precisely, if
and the chain goes to infinity, a.s. More precisely, if 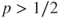 , then as previously shown
, then as previously shown 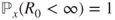 for
for  , and thus
, and thus  . Similarly, if
. Similarly, if 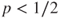 , then
, then 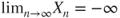 .
.
- 2.9.f Then,
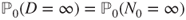 and we conclude by a previous result.
and we conclude by a previous result.
If
 a.s., then
a.s., then 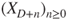 cannot hit
cannot hit 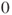 , and hence does not have same law as
, and hence does not have same law as  . By contradiction,
. By contradiction, 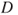 cannot be a stopping time, as then the strong Markov property would have applied.
cannot be a stopping time, as then the strong Markov property would have applied. - 2.9.g Then,
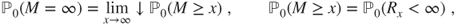
and previous results allow to conclude.
If
 , then
, then  cannot reach a state greater than its initial value, and hence does not have same law as
cannot reach a state greater than its initial value, and hence does not have same law as 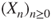 . By contradiction,
. By contradiction,  cannot be a stopping time, as then the strong Markov property would have applied.
cannot be a stopping time, as then the strong Markov property would have applied. - 2.9.h If
 , then
, then 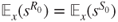 , hence the result. The result for
, hence the result. The result for 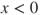 is obtained by symmetry.
is obtained by symmetry.
- 2.9.i The “one step forward” method yields that
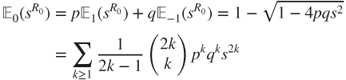
- in which we use the classic Taylor expansion provided at the end of Section 2.3.2. By identification,
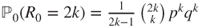 for
for  .
.
- 2.10.a We have
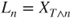 for
for  .
.
- 2.10.b Straightforward, notably
 is clearly irreducible.
is clearly irreducible.
- 2.10.c The “one step forward” method (Theorem 2.2.2) yields the equation. Its characteristic polynomial is
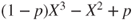 , and its roots are
, and its roots are 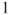 and
and  and
and 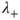 . This yields the general solution, considering the case of multiple roots.
. This yields the general solution, considering the case of multiple roots.
- 2.10.d We have only two boundary conditions, whereas the space of general solutions is of dimension three, so we must use the minimality result in Theorem 2.(2.2 to find the solution of interest.
- 2.10.e We use Theorem 2.(2.6 and seek the least solution with values in
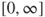 . We use the above-mentioned general solution for the associated linear equation, and a particular solution of the form
. We use the above-mentioned general solution for the associated linear equation, and a particular solution of the form  when
when 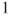 is a simple root and
is a simple root and  if it is a double.
if it is a double.
- 2.10.f We may use Theorem 2.2.5, but we do not have a trivial solution for the characteristic polynomial of degree three
 for the linear recursion.
for the linear recursion.
