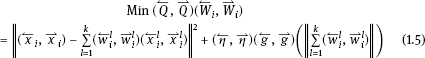1.2.2.3Improved locally linear embedding (ILLE)
Determining the size of the neighbourhood k is a very important problem. If k is too small, the mapping will cause the sub-manifolds to break away from the continuous manifold and not reflect any global properties. If k is too large, the entire dataset will be considered as the local neighbourhood, and the map will lose its nonlinear characteristic [15]. In this section, we propose an ILLE method that uses the diffusion and growing self-organizing map (DGSOM) [16] to define neighbourhood relations. For example, if a point has five associated points in the DGSOM map, the five data points are considered neighbours of that point. Thus, the size of the neighbourhood of each sample point, k, is different, which overcomes the shortcoming of the traditional LLE method that the neighbourhood size of each point is fixed. In addition, the ILLE reduces the influence of noise by reducing the noise interference and weighting energy. By way of example, we show that ILLE can adapt to the neighbourhood and overcome the sensitivity problem, enabling it to solve the error problem caused by the three factors identified above.
The core of the ILLE method is to seek the k-dimensional dynamic fuzzy vector (←Wi,←Wi)=((←W1i,←W1i),(←W2i,←W2i),...,(←Wki,←Wki)).(W←−i,W←−i)=((W←−1i,W←−1i),(W←−2i,W←−2i),...,(W←−ki,W←−ki)). The optimization problem is
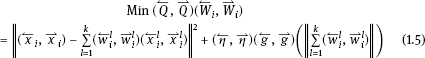

which is to find the corresponding dynamic fuzzy topology matrix ( ,
,  ), and finally get (↼MM↼−, ⇀MM−⇀).
), and finally get (↼MM↼−, ⇀MM−⇀).
ILLE avoids the ill-posedness of LLE by introducing the dynamic fuzzy regularization term (←g,→g)(‖k∑l=1(←wli,←wli)‖),(g←,g→)(∥∥∥∥∑l=1k(w←li,w←li)∥∥∥∥), which reduces the influence of noise interference. This term must satisfy two points: (1) (1.5) must have a steady solution; and (2) ‖k∑l=1(←wli,←wli)‖∥∥∥∥∑l=1k(w←li,w←li)∥∥∥∥ in (1.5) must be minimized, typically such that (←g,→g)(←x,→x)=(g←,g→)(x←,x→)=(←x,→x)2,(←η,→η)(x←,x→)2,(η←,η→) is the improvement factor, which is related to the neighbourhood number k, the dimension of the dynamic fuzzy dataset D, and the dimension of the dynamic fuzzy dataset. We can see from the calculation that the choice of (←η,→η)(η←,η→) does not have a large effect on the outcome. The description of ILLE is shown in Algorithm 1.1.
Algorithm 1.1 ILLE algorithm
Input: (←x,→x)={(←x1,←x1),(←x2,←x2),...,(←xn,←xn)}⊂(←RD×n,←RD×n),(x←,x→)={(x←1,x←1),(x←2,x←2),...,(x←n,x←n)}⊂(R←D×n,R←D×n),(←xj,→xi)∈(←RD,←RD)(i=1,2,...,n)(x←j,x→i)∈(R←D,R←D)(i=1,2,...,n)
Output:(←Y,→Y)={(←Y1,→Y1),(←Y2,→Y2),(←Yn,→Yn)}⊂(←Rd×n,←Rd×n),(Y←,Y→)={(Y←1,Y→1),(Y←2,Y→2),(Y←n,Y→n)}⊂(R←d×n,R←d×n),(←yj,→yj)∈(←Rd,←Rd)(l=1,2,...,n)(y←j,y→j)∈(R←d,R←d)(l=1,2,...,n)
For each (←xj,←xj)(x←j,x←j) do
1.Choose neighbourhood: The k neighbourhoods {(←x1i,←x1i)|=1,2,...,k}{(x←1i,x←1i)∣∣∣=1,2,...,k} of each point (←xi,→xi)(x←i,x→i) are determined according to the DGSOM method, where k may be different for each neighbourhood. A linear combination of {(←x1j,←x1j)|l=1,2,...,k}{(x←1j,x←1j)∣∣∣l=1,2,...,k} is used to denote (←xi,←xi),(x←i,x←i), that is, the hyperboloid passing through {(←x1j,←x1j)|l=1,2,...,k}{(x←1j,x←1j)∣∣∣l=1,2,...,k} is used to approximate the local block near {(←xij,←xij)|l=1,2,...,k}{(x←ij,x←ij)∣∣∣l=1,2,...,k} in the manifold.
2.Get weight: For each (←xi,←xi),find(←Wi,←Wi)=((←W1j,←W1j),(←W2j,←W2j),...,(←Wkj,←Wkj))(x←i,x←i),find(W←−i,W←−i)=((W←−1j,W←−1j),(W←−2j,W←−2j),...,(W←−kj,W←−kj)) that minimizes (←Q,←Q)(←wi,←wi)=‖(←xi,←xi)−k∑i=1(←wli,←wli)(←x1i,←x1i)‖2+(←η,→η)‖k∑l=1(←w1i,←w1i)‖2.(Q←,Q←)(w←i,w←i)=∥∥∥(x←i,x←i)−∑i=1k(w←li,w←li)(x←1i,x←1i)∥∥∥2+(η←,η→)∥∥∥∥∑l=1k(w←1i,w←1i)∥∥∥∥2. and finally obtain the dynamic fuzzy topology matrix ( ,
,  ).
).
3. Reduce dimension: Minimize the loss function

where (←Y,→Y)=((←Y1,→Y2),(←Y2,→Y2),...,(←Yn,→Yn))∈(←Rd×n,←Rd×n),(←yi,←yi)∈(←Rd,←Rd)(i=)(Y←,Y→)=((Y←1,Y→2),(Y←2,Y→2),...,(Y←n,Y→n))∈(R←d×n,R←d×n),(y←i,y←i)∈(R←d,R←d)(i=) 1,2,. . .n). To make the solution unique, we add the constraint to (←Yi,←Yi)∈(←Rd,←Rd)(i=(Y←i,Y←i)∈(R←d,R←d)(i= 1,2,. . .n):

where (←I,→I)d×d(I←,I→)d×d is the dynamic fuzzy unit matrix.
The computational complexity of each step of ILLE is as follows. The number of computations in steps 1–3 is O(Dn2, ODnk3, and Odn2, respectively. The computational complexity of ILLE is similar to that of LLE, but ILLE is more robust against noise interference.
1.2.2.4DFML algorithm and its stability analysis
A. DFML Algorithm [, , , 11]
Consider the DFMLS set up by the following dynamic fuzzy rules:
Rl: IF (←x,→x)(k) is (←Al1,←Al1)(x←,x→)(k) is (A←l1,A←l1) is (←x,→x)(k−1)(x←,x→)(k−1) and (←Al2,←Al2)(A←l2,A←l2) is (←x,→x)(x←,x→) and ...and (←x,→x)(x←,x→)(k−n+1)(k−n+1) is (←A1n,←A1n)(A←1n,A←1n) and (←u,→u)(k)is(←Bl,←Bl)(u←,u→)(k)is(B←l,B←l) THEN

where (←X,→X)(k)=((←x,→x)(k),(←x,→x)(k−1),...,(←x,→x)(k−n+1))T∈(←U,→U)(X←,X→)(k)=((x←,x→)(k),(x←,x→)(k−1),...,(x←,x→)(k−n+1))T∈(U←,U→) is the system state vector, (←Al,←Al)=((←al1,←al1),(←al2,←al2),...,(←aln,←aln)),(←ali,←ali)(A←l,A←l)=((a←l1,a←l1),(a←l2,a←l2),...,(a←ln,a←ln)),(a←li,a←li) (i = 1, 2, ..., n) is the corresponding dynamic fuzzy constant, and (←Ali,←Ali)∈(A←li,A←li)∈(←R,→R)n×n,(←Bt,→Bt)∈(←R,→R)n×n(R←,R→)n×n,(B←t,B→t)∈(R←,R→)n×n is the dynamic fuzzy constant matrix. The linear state equation corresponding to each dynamic fuzzy rule is called the DFML subsystem.
For the problem of noise in the learning process, we use the robust factor proposed in [17] to reduce the interference:

where (←ei,→ej)=(←yd,←yd)−(←yi,←yi),(←yd,←yd)(e←i,e→j)=(y←d,y←d)−(y←i,y←i),(y←d,y←d) is the expectation output, (←yi,→yi)(y←i,y→i) is the actual output, and (←ci,←ci)(c←i,c←i) is the central value of the confidence interval for the statistical estimation of the deviation (←Stdak,cur,←Stdak,cur)(Std←−−ak,cur,Std←−−ak,cur)(←Gak,cur,←Gak,cur)(G←ak,cur,G←ak,cur) is a nonnegative integrable function of (←Ck,→Ck):(C←k,C→k): and
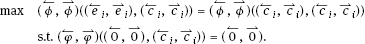
The learning algorithm of the DFMLS is shown in Algorithm 1.2.
Algorithm 1.2 Dynamic fuzzy machine learning
Input: (←x,→x)(x←,x→)
Output: (←yk,←yk)(y←k,y←k)
//(←u←Ajl,←u←Ajl),(←u←bjl,←u→bjl)//(u←A←jl,u←A←jl),(u←b←jl,u←b→jl) is the corresponding dynamic fuzzy membership, (←yd,←yd)(y←d,y←d) is the desired output //
(1)Use the ILLE method to reduce the dimension of the DFD;
(2)

(3)(→v,←v)l=n∏j=1(←u←A1j,←u←A1j)[(←x,→x)(k−l+1)](←u→b1j,←u←b1j)[(←u,→u)(k)];(v→,v←)l=∏j=1n(u←A←1j,u←A←1j)[(x←,x→)(k−l+1)](u←b→1j,u←b←1j)[(u←,u→)(k)];
(4)(←yk,→yk)=k∑j−1(←hj,←hj)(←x,→x)(i)k∑j−1(←hj,←hj);(y←k,y→k)=∑j−1k(h←j,h←j)(x←,x→)(i)∑j−1k(h←j,h←j);
(5)(←ek,←ek)=(←yd,←yd)−(←yk,←yk);(e←k,e←k)=(y←d,y←d)−(y←k,y←k);
(6)(←ϕ,→ϕ)((←ek,←ek)(←ck,←ck))=2.exp(−(←λk,←λk)|(←ek,←ek)−(←ck,←ck)|);(ϕ←,ϕ→)((e←k,e←k)(c←k,c←k))=2.exp(−(λ←k,λ←k)∣∣(e←k,e←k)−(c←k,c←k)∣∣);//(←λk,←λk)and(←ck,←ck)//(λ←k,λ←k)and(c←k,c←k) are determined as in [17] //
(7)(←p,→p)(k)=12k∑j=1|(←ei,←ei)|2;//performance//(p←,p→)(k)=12∑j=1k∣∣(e←i,e←i)∣∣2;//performance//
(8)if|(←ek,←ek)>(←ε,→ε)|.if∣∣(e←k,e←k)>(ε←,ε→)∣∣.
//(←ε,→ε)(ε←,ε→) is the maximum tolerance error, its value can be based on system requirements or experience. If the learning error is greater than the maximum tolerance, then the learning is invalid//
then Discard (←yk,←yk),(y←k,y←k), feedback to the rule base, notify the adjustment rules of the parameters, perform a parametric learning algorithm.
(←u,→u)(k)=(←u,→u)(k)+α(←ek,←ek)(u←,u→)(k)=(u←,u→)(k)+α(e←k,e←k) //α is the gain learning coefficient
Continue from scratch
else if | (←ek,←ek)≤(←δ,→δ)|(e←k,e←k)≤(δ←,δ→)∣∣∣
//(←δ,→δ)(δ←,δ→) is an acceptable error, much smaller than (→ε,←ε),(ε→,ε←),, its value can be given according to system requirements or experience. If the error after learning is less than (or equal to) this acceptable level, it is considered to have reached the accuracy of the learning requirements //
then The learning process is finished, corrected, and output
(←yk,←yk)=(←yk,←yk)+β(←ϕ,→ϕ)((←ek,←ek)(←ck,←ck))=(←yk,←yk)//β(y←k,y←k)=(y←k,y←k)+β(ϕ←,ϕ→)((e←k,e←k)(c←k,c←k))=(y←k,y←k)//β is the correction factor
else Feedback to the rule base, notify the adjustment rules in the parameters, and implement the parameter learning algorithm.

Continue from scratch;
end if
end if
Note: (←hj,←hj)(h←j,h←j) is the corresponding weight coefficient, and the membership function is generally taken as the weight coefficient.
B. Stability analysis
Denoting ( ,
,  )(k) as ((←x,←x)(k),(←x,←x)(k−1),...,(←x,←x)(k−n+1))T∈(←U,→U)((x←,x←)(k),(x←,x←)(k−1),...,(x←,x←)(k−n+1))T∈(U←,U→) and
)(k) as ((←x,←x)(k),(←x,←x)(k−1),...,(←x,←x)(k−n+1))T∈(←U,→U)((x←,x←)(k),(x←,x←)(k−1),...,(x←,x←)(k−n+1))T∈(U←,U→) and

![]()
![]() ,
, ![]() ) is mainly determined by three factors: (1) the influence of noise interference, that is, the size of (←δ,→δ);
) is mainly determined by three factors: (1) the influence of noise interference, that is, the size of (←δ,→δ);![]() ,
, ![]() ), and finally get (↼M
), and finally get (↼M![]() ,
, ![]() ).
).
![]()
![]()
![]() ,
, ![]() )(k) as ((←x,←x)(k),(←x,←x)(k−1),...,(←x,←x)(k−n+1))T∈(←U,→U)
)(k) as ((←x,←x)(k),(←x,←x)(k−1),...,(←x,←x)(k−n+1))T∈(←U,→U)