Perhaps the most elementary vector spaces are the Euclidean vector spaces ${ℝ}^n$, $n=1,2,\dots$. For simplicity, let us consider first ${ℝ}^2$. Nonzero vectors in ${ℝ}^2$ can be represented geometrically by directed line segments. This geometric representation will help us to visualize how the operations of scalar multiplication and addition work in ${ℝ}^2$. Given a nonzero vector $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$, we can associate it with the directed line segment in the plane from (0, 0) to $(x_1,x_2)$ (see Figure 3.1.1). If we equate line segments that have the same length and direction (Figure 3.1.2), x can be represented by any line segment from $(a,b)$ to $(a+x_1,b+x_2)$.

Figure 3.1.1.

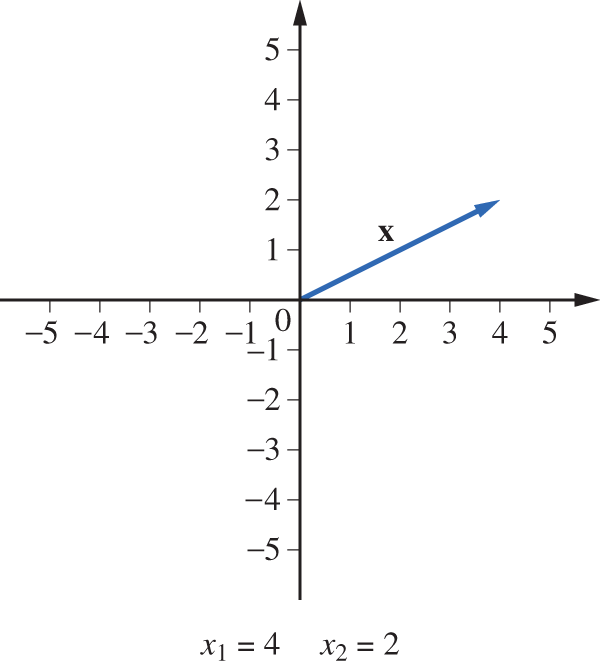
Figure 3.1.2.

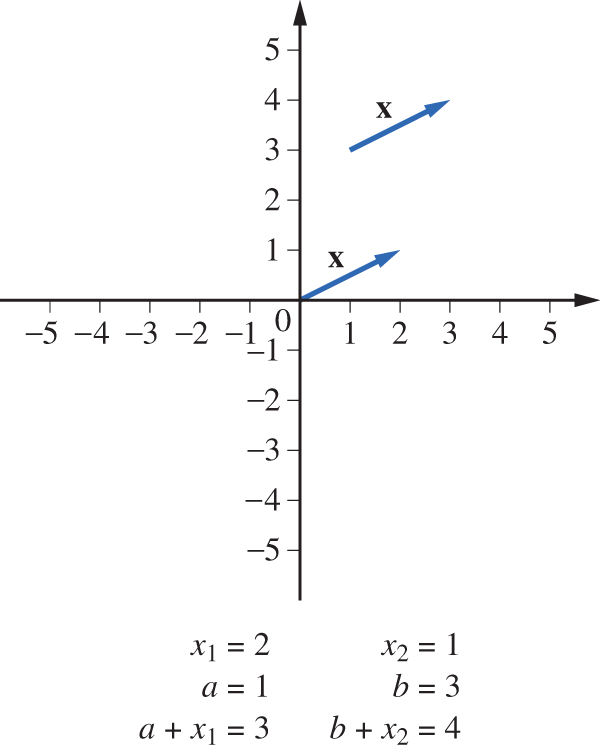
For example, the vector $\mathbf{x}=\left[\begin{array}{c}2\\ 1\end{array}\right]$ in ${ℝ}^2$ could just as well be represented by the directed line segment from $(2,2)$ to $(4,3)$ or from $(-1,-1)$ to $(1,0)$, as shown in Figure 3.1.3.

Figure 3.1.3.

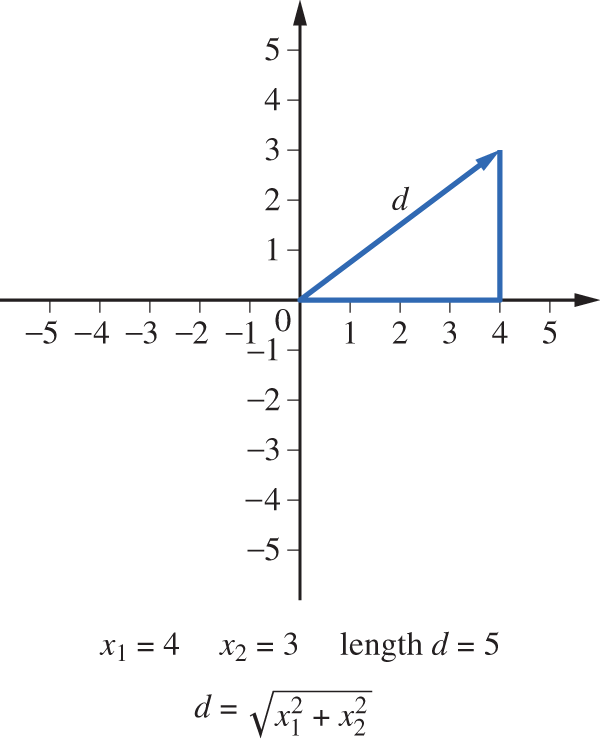
We can think of the Euclidean length of a vector $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$ as the length of any directed line segment representing x. The length of the line segment from $(0,0)$ to $(x_1,x_2)$ is $\sqrt{x_1^2+x_2^2}$ (see Figure 3.1.4). For each vector $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$ and each scalar $\alpha$, the product $\alpha \mathbf{x}$ is defined by

Figure 3.1.4.

For example, as shown in Figure 3.1.5, if $\mathbf{x}=\left[\begin{array}{c}2\\ 1\end{array}\right]$, then

Figure 3.1.5.

The vector 3x is in the same direction as x, but its length is three times that of x. The vector $-\mathbf{x}$ has the same length as x, but it points in the opposite direction. The vector $-2\mathbf{x}$ is twice as long as x and it points in the same direction as $-\mathbf{x}$. The sum of two vectors

is defined by

Note that if v is placed at the terminal point of u, then $\mathbf{u}+\mathbf{v}$ is represented by the directed line segment from the initial point of u to the terminal point of v (Figure 3.1.6). If both u and v are placed at the origin and a parallelogram is formed as in Figure 3.1.7, the diagonals of the parallelogram will represent the sum $\mathbf{u}+\mathbf{v}$ and the difference $\mathbf{v}-\mathbf{u}$. In a similar manner, vectors in ${ℝ}^3$ can be represented by directed line segments in 3-space (see Figure 3.1.8).

Figure 3.1.6.

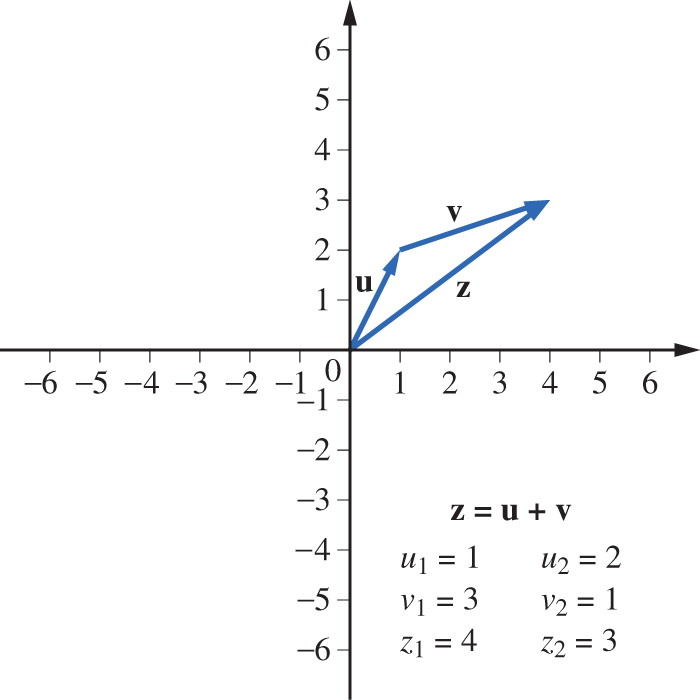
Figure 3.1.7.

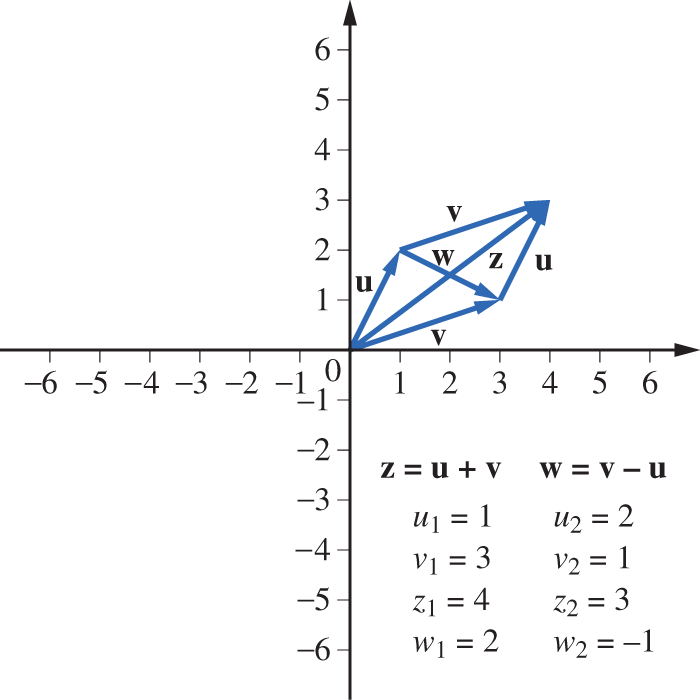
Figure 3.1.8.

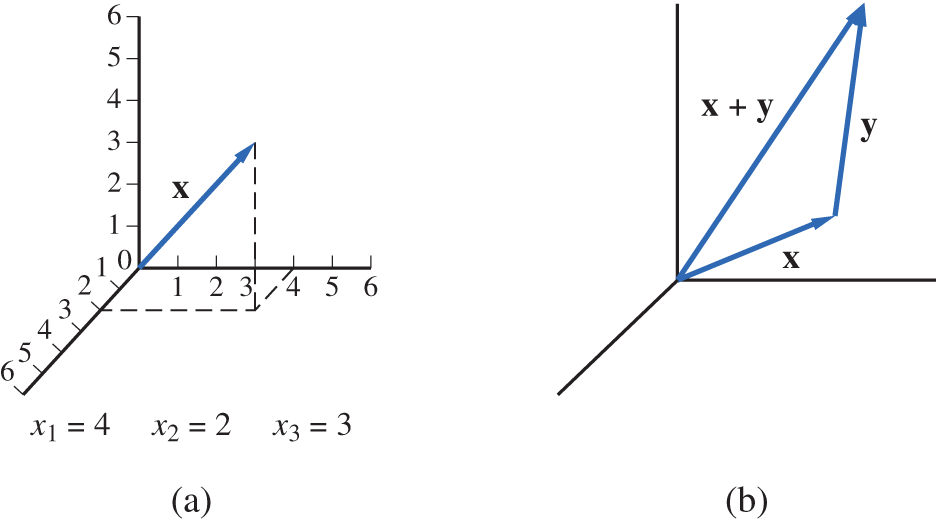
In general, scalar multiplication and addition in ${ℝ}^n$ are, respectively, defined by

for any x, y ∈ ${ℝ}^n$ and any scalar $\alpha$.

We can also view ${ℝ}^n$ as the set of all n × 1 matrices with real entries. The addition and scalar multiplication of vectors in ${ℝ}^n$ are just the usual addition and scalar multiplication of matrices. More generally, let ${ℝ}^{m\times n}$ denote the set of all $m\times n$ matrices with real entries. If $A=\left(a_{ij}\right)$ and $B=\left(b_{ij}\right)$, then the sum $A+B$ is defined to be the $m\times n$ matrix $C=\left(c_{ij}\right)$, where $c_{ij}=a_{ij}+b_{ij}$. Given a scalar $\alpha$, we can define αA to be the $m\times n$ matrix whose $(i,j)$ entry is $\alpha a_{ij}$. Thus, by defining operations on the set ${ℝ}^{m\times n}$, we have created a mathematical system. The operations of addition and scalar multiplication of ${ℝ}^{m\times n}$ obey certain algebraic rules. These rules form the axioms that are used to define the concept of a vector space.

We will refer to the set V as the universal set for the vector space. Its elements are called vectors and are usually denoted by boldface letters such as u, v, w, x, y, and z. The term scalar will generally refer to a real number, although in some cases it will be used to refer to complex numbers. Scalars will generally be represented by lowercase italic letters such as a, b, and c or lowercase Greek letters such as $\alpha$, $\beta$, and $\gamma$. In the first five chapters of this book, the term scalars will always refer to real numbers. Often the term real vector space is used to indicate that the set of scalars is the set of real numbers. The boldface symbol 0 was used in Axiom 3 in order to distinguish the zero vector from the scalar 0.

An important component of the definition is the closure properties of the two operations. These properties can be summarized as follows:

• C1. If $\mathbf{x}\in V$ and $\alpha$ is a scalar, then $\alpha \mathbf{x}\in V$.

• C2. If $\mathbf{x},\mathbf{y}\in V$, then $\mathbf{x}+\mathbf{y}\in V$.

To illustrate the necessity of the closure properties, consider the following example. Let

with addition and scalar multiplication defined in the usual way. The elements $(3,1)$ and $(5,1)$ are in W, but the sum

is not an element of W. The operation + is not really an operation on the set W because property C2 fails to hold. Similarly, scalar multiplication is not defined on W, because property C1 fails to hold. The set W, together with the operations of addition and scalar multiplication, is not a vector space.

If, however, we are given a set U on which the operations of addition and scalar multiplication have been defined and satisfy properties C1 and C2, then we must check to see if the eight axioms are valid in order to determine whether U is a vector space. We leave it to the reader to verify that ${ℝ}^n$ and ${ℝ}^{m\times n}$, with the usual addition and scalar multiplication of matrices, are both vector spaces. There are a number of other important examples of vector spaces.

Let $C[a,b]$ denote the set of all real-valued functions that are defined and continuous on the closed interval $[a,b]$. In this case, our universal set is a set of functions. Thus, our vectors are the functions in $C[a,b]$. The sum $f+g$ of two functions in $C[a,b]$ is defined by

for all x in $[a,b]$. The new function $f+g$ is an element of $C[a,b]$ since the sum of two continuous functions is continuous. If f is a function in $C[a,b]$ and $\alpha$ is a real number, define αf by

for all x in $[a,b]$. Clearly, αf is in $C[a,b]$ since a constant times a continuous function is always continuous. Thus, we have defined the operations of addition and scalar multiplication on $C[a,b]$. To show that the first axiom, $f+g=g+f$, is satisfied, we must show that

This follows because

for every x in $[a,b]$. Axiom 3 is satisfied, since the function

acts as the zero vector; that is,

We leave it to the reader to verify that the remaining vector space axioms are all satisfied.

Let $P_n$ denote the set of all polynomials of degree less than n. Define $p+q$ and αp, respectively, by

and

for all real numbers x. In this case, the zero vector is the zero polynomial:

It is easily verified that all the vector space axioms hold. Thus, $P_n$, with the standard addition and scalar multiplication of functions, is a vector space.

We close this section with a theorem that states three more fundamental properties of vector spaces. Other important properties are given in Exercises 7, 8, and 9 at the end of the section.

Proof

It follows from axioms A6 and A8 that

Thus,

To prove (ii), suppose that $\mathbf{x}+\mathbf{y}=\mathbf{0}$. Then

Therefore,

Finally, to prove (iii), note that

Thus,

and it follows from part (ii) that

∎