3.5 Change of Basis
Many applied problems can be simplified by changing from one coordinate system to another. Changing coordinate systems in a vector space is essentially the same as changing from one basis to another. For example, in describing the motion of a particle in the plane at a particular time, it is often convenient to use a basis for consisting of a unit tangent vector t and a unit normal vector n instead of the standard basis .
In this section, we discuss the problem of switching from one coordinate system to another. We will show that this can be accomplished by multiplying a given coordinate vector x by a nonsingular matrix S. The product will be the coordinate vector for the new coordinate system.
Changing Coordinates in
The standard basis for is . Any vector x in can be expressed as a linear combination:
The scalars and can be thought of as the coordinates of x with respect to the standard basis. Actually, for any basis for , it follows from Theorem 3.3.2 that a given vector x can be represented uniquely as a linear combination:
The scalars and are the coordinates of x with respect to the basis . Let us order the basis elements so that y is considered the first basis vector and z is considered the second, and denote the ordered basis by . We can then refer to the vector as the coordinate vector of x with respect to . Note that, if we reverse the order of the basis vectors and take , then we must also reorder the coordinate vector. The coordinate vector of x with respect to will be . When we refer to a basis using subscripts, such as , the subscripts assign an ordering to the basis vectors.
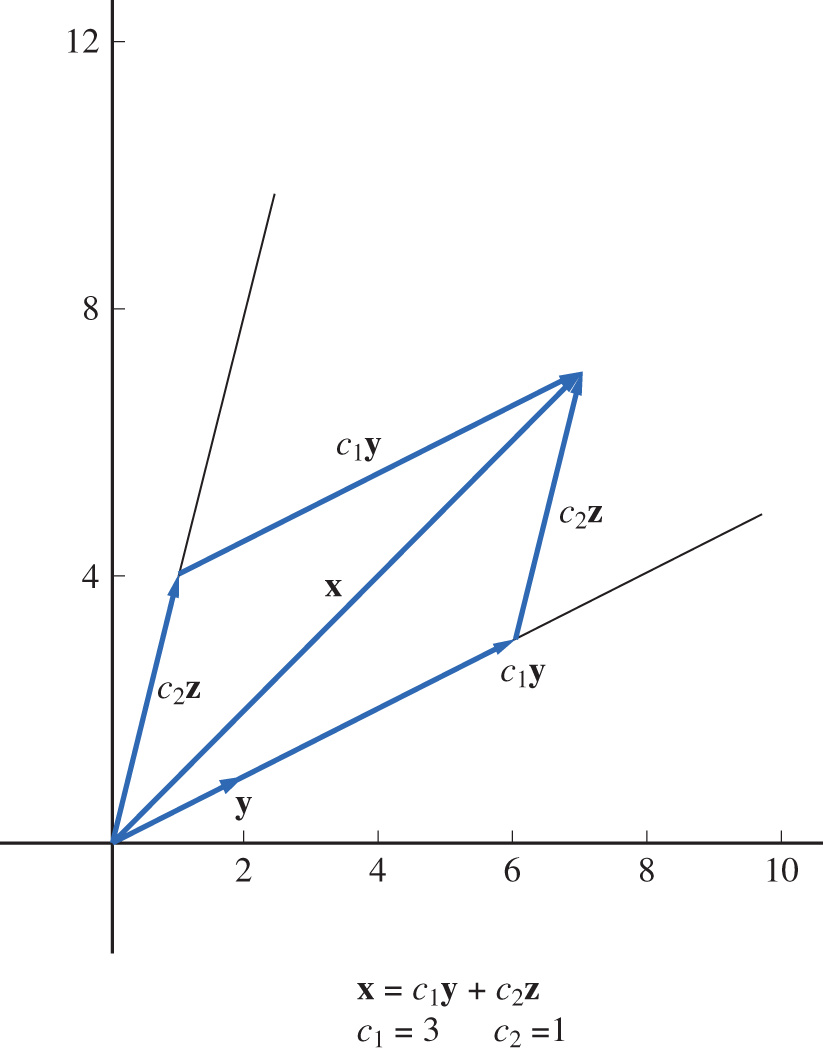
Example 1
Let and . The vectors y and z are linearly independent and hence form a basis for . The vector can be written as a linear combination:
Thus, the coordinate vector of x with respect to is . Geometrically, the coordinate vector specifies how to get from the origin to the point by moving first in the direction of y and then in the direction of z. If, instead, we treat z as our first basis vector and y as the second basis vector, then
The coordinate vector of x with respect to the ordered basis is . Geometrically, this vector tells us how to get from the origin to by moving first in the direction of z and then in the direction of y (see Figure 3.5.1).
Figure 3.5.1.
As an example of a problem for which it is helpful to change coordinates, consider the following application.
Changing Coordinates
Once we have decided to work with a new basis, we have the problem of finding the coordinates with respect to that basis. Suppose, for example, that instead of using the standard basis for , we wish to use a different basis, say,
Indeed, we may want to switch back and forth between the two coordinate systems. Let us consider the following two problems:
Given a vector , find its coordinates with respect to and .
Given a vector , find its coordinates with respect to and .
We will solve II first, since it turns out to be the easier problem. To switch bases from to , we must express the old basis elements and in terms of the new basis elements and .
It follows then that
Thus, the coordinate vector of with respect to is
If we set
then, given any coordinate vector c with respect to , to find the corresponding coordinate vector x with respect to , we simply multiply U times c:
The matrix U is called the transition matrix from the ordered basis to the standard basis .
To solve problem I, we must find the transition matrix from to . The matrix U in (2) is nonsingular, since its column vectors, and , are linearly independent. It follows from (2) that
Thus, given a vector
we need only multiply by to find its coordinate vector with respect to . is the transition matrix from to .
Example 2
Let , and . Find the coordinates of x with respect to and .
SOLUTION
By the preceding discussion, the transition matrix from to is the inverse of
Thus,
is the desired coordinate vector and
Example 3
Let and . Find the transition matrix from to and determine the coordinates of with respect to .
SOLUTION
The transition matrix from to is
and hence the transition matrix from to is
The coordinate vector of x with respect to is
and hence
Now let us consider the general problem of changing from one ordered basis of to another ordered basis . In this case, we assume that, for a given vector x, its coordinates with respect to are known:
Now we wish to represent x as a sum . Thus, we must find scalars and so that
If we set and , then Equation (3) can be written in matrix form:
It follows that
Thus, given a vector x in and its coordinate vector c with respect to the ordered basis , to find the coordinate vector of x with respect to the new basis , we simply multiply c by the transition matrix .
Example 4
Find the transition matrix corresponding to the change of basis from to , where
SOLUTION
The transition matrix from to is given by
The change of basis from to can also be viewed as a two-step process. First we change from to the standard basis, , and then we change from the standard basis to . Given a vector x in , if c is the coordinate vector of x with respect to and d is the coordinate vector of x with respect to , then
Since V is the transition matrix from to and is the transition matrix from to , it follows that
and hence
As before, we see that the transition matrix from to is (see Figure 3.5.2).
Figure 3.5.2.

Change of Basis for a General Vector Space
Everything we have done so far can easily be generalized to apply to any finite-dimensional vector space. We begin by defining coordinate vectors for an n-dimensional vector space.
The examples considered so far have all dealt with changing coordinates in . Similar techniques could be used for . In the case of , the transition matrices will be .
Example 5
If
and
then and are ordered bases for . Let
Find the transition matrix from E to F and use it to find the coordinates of x and y with respect to the ordered basis F.
SOLUTION
As in Example 4, the transition matrix is given by
The coordinate vectors of x and y with respect to the ordered basis F are given by
and
The reader may verify that
If V is any n-dimensional vector space, it is possible to change from one basis to another by means of an transition matrix. We will show that such a transition matrix is necessarily nonsingular. To see how this is done, let and be two ordered bases for V. The key step is to express each basis vector as a linear combination of the .
Let . If , it follows from (4) that
Thus, if , then
and hence,
The matrix S defined by (4) is referred to as the transition matrix. Once S has been determined, it is a simple matter to change coordinate systems. To find the coordinates of with respect to , we need only calculate .
The transition matrix S corresponding to the change of basis from to can be characterized by the condition
Taking in (5), we see that implies that
Since the are linearly independent, it follows that . Thus, the equation has only the trivial solution and hence the matrix S is nonsingular. The inverse matrix is characterized by the condition
Thus, is the transition matrix used to change basis from to .
Example 6
Suppose that in we want to change from the ordered basis to the ordered basis . Because is the standard basis for , it is easier to find the transition matrix from to . Since
the transition matrix is
The inverse of S will be the transition matrix from to :
Given any in , to find the coordinates of with respect to , we multiply
Thus,
We have seen that each transition matrix is nonsingular. Actually, any nonsingular matrix can be thought of as a transition matrix. If S is an nonsingular matrix and is an ordered basis for V, then define by (4). To see that the are linearly independent, suppose that
It follows from (4) that
By the linear independence of the , it follows that
or, equivalently,
Since S is nonsingular, x must equal 0. Therefore, are linearly independent and hence they form a basis for V. The matrix S is the transition matrix corresponding to the change from the ordered basis to .
In many applied problems, it is important to use the right type of basis for the particular application. In Chapter 5, we will see that the key to solving least squares problems is to switch to a special type of basis called an orthonormal basis. In Chapter 6, we will consider a number of applications involving the eigenvalues and eigenvectors associated with an matrix A. The key to solving these types of problems is to switch to a basis for consisting of eigenvectors of A.
