5.1 The Scalar Product in
Two vectors x and y in may be regarded as matrices. We can then form the matrix product . This product is a matrix that may be regarded as a vector in or, more simply, as a real number. The product is called the scalar product of x and y. In particular, if and , then
Example 1
If
then
The Scalar Product in and
In order to see the geometric significance of the scalar product, let us begin by restricting our attention to and . Vectors in and can be represented by directed line segments. Given a vector x in either or , its Euclidean length can be defined in terms of the scalar product.
Given two nonzero vectors x and y, we can think of them as directed line segments starting at the same point. The angle between the two vectors is then defined as the angle between the line segments. We can measure the distance between the vectors by measuring the length of the vector joining the terminal point of x to the terminal point of y (see Figure 5.1.1). Thus, we have the following definition.
Figure 5.1.1.
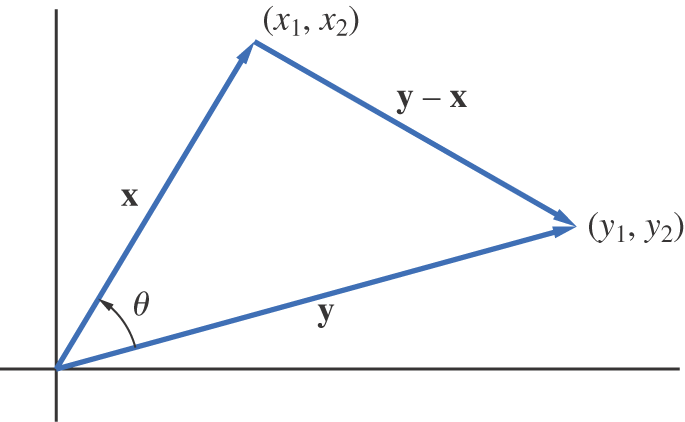
Example 2
If and , then the distance between x and y is given by
The angle between two vectors can be computed using the following theorem.
Theorem 5.1.1
If x and y are two nonzero vectors in either or and is the angle between them, then
Proof
The vectors x, y, and may be used to form a triangle as in Figure 5.1.1. By the law of cosines, we have
and hence it follows that
∎
If x and y are nonzero vectors, then we can specify their directions by forming unit vectors
If is the angle between x and y, then
The cosine of the angle between the vectors x and y is the scalar product of the corresponding direction vectors u and v.
Example 3
Let x and y be the vectors in Example 2. The directions of these vectors are given by the unit vectors
The cosine of the angle between the two vectors is
and hence .
Corollary 5.1.2 Cauchy—Schwarz Inequality
If x and y are vectors in either or , then
with equality holding if and only if one of the vectors is 0 or one vector is a multiple of the other.
Proof
The inequality follows from (1). If one of the vectors is 0, then both sides of (2) are 0. If both vectors are nonzero, it follows from (1) that equality can hold in (2) if and only if . But this would imply that the vectors are either in the same or opposite directions and hence that one vector must be a multiple of the other.
∎
If , it follows from Theorem 5.1.1 that either one of the vectors is the zero vector or . If , the angle between the vectors is a right angle.
Example 4
The vector 0 is orthogonal to every vector in .
The vectors and are orthogonal in .
The vectors and are orthogonal in .
Scalar and Vector Projections
The scalar product can be used to find the component of one vector in the direction of another. Let x and y be nonzero vectors in either or . We would like to write x as a sum of the form , where p is in the direction of y and z is orthogonal to p (see Figure 5.1.2). To do this, let . Thus, u is a unit vector (length 1) in the
Figure 5.1.2.
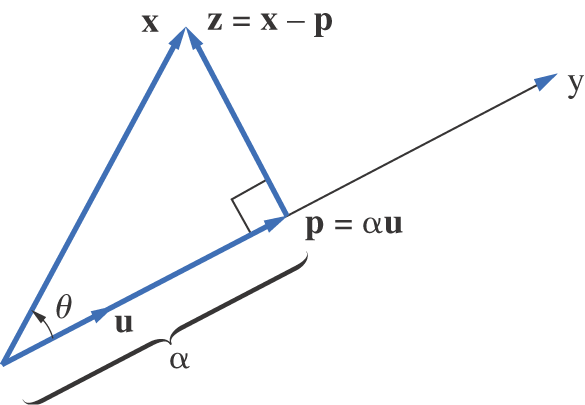
direction of y. We wish to find such that is orthogonal to . For p and z to be orthogonal, the scalar must satisfy
The scalar α is called the scalar projection of x onto y, and the vector p is called the vector projection of x onto y.
Scalar projection of x onto y:
Vector projection of x onto y:
Example 5
The point Q in Figure 5.1.3 is the point on the line that is closest to the point (1, 4). Determine the coordinates of Q.
Figure 5.1.3.
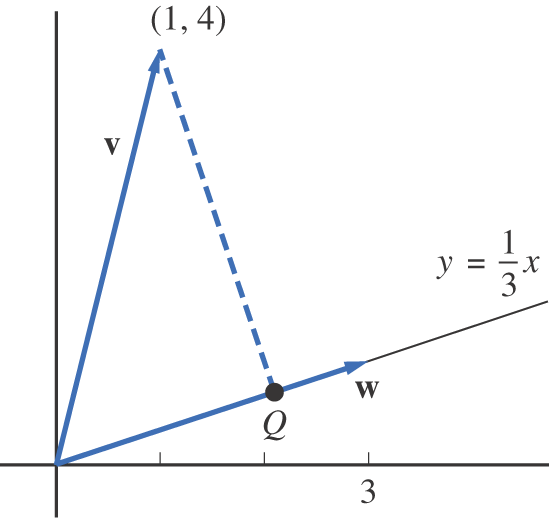
SOLUTION
The vector is a vector in the direction of the line . Let . If Q is the desired point, then is the vector projection of v onto w.
Thus, is the closest point.
Notation
If and are two points in 3-space, we will denote the vector from to by .
If N is a nonzero vector and is a fixed point, the set of points P such that is orthogonal to N forms a plane π in 3-space that passes through . The vector N and the plane π are said to be normal to each other. A point will lie on π if and only if
If and , this equation can be written in the form
Example 6
Find the equation of the plane passing through the point and normal to the vector .
SOLUTION
. The equation is , or
The span of two linearly independent vectors x and y in corresponds to a plane through the origin in 3-space. To determine the equation of the plane, we must find a vector normal to the plane. In Section 2.3, it was shown that the cross product of the two vectors is orthogonal to each vector. If we take as our normal vector, then the equation of the plane is given by
Example 7
Find the equation of the plane that passes through the points
SOLUTION
Let
The normal vector N must be orthogonal to both x and y. If we set
then N will be a normal vector to the plane that passes through the given points. We can then use any one of the points to determine the equation of the plane. Using the point , we see that the equation of the plane is
Example 8
Find the distance from the point (2, 0, 0) to the plane .
SOLUTION
The vector is normal to the plane and the plane passes through the origin. Let . The distance d from (2, 0, 0) to the plane is simply the absolute value of the scalar projection of v onto N. Thus,
If x and y are nonzero vectors in and is the angle between the vectors, then
It then follows that
and hence
Thus, we have, for any nonzero vectors x and y in ,
If either x or y is the zero vector, then and hence the norm of will be 0.
Orthogonality in
The definitions that have been given for and can all be generalized to . Indeed, if , then the Euclidean length of x is defined by
If x and y are two vectors in , then the distance between the vectors is .
The Cauchy–Schwarz inequality holds in . (We will prove this in Section 5.4.) Consequently,
for any nonzero vectors x and y in . In view of (3), the definition of the angle between two vectors that was used for can be generalized to . Thus, the angle between two nonzero vectors x and y in is given by
In talking about angles between vectors, it is usually more convenient to scale the vectors so as to make them unit vectors. If we set
then the angle between u and v is clearly the same as the angle between x and y, and its cosine can be computed simply by taking the scalar product of the two unit vectors:
The vectors x and y are said to be orthogonal if . Often the symbol ⊥ is used to indicate orthogonality. Thus, if x and y are orthogonal, we will write . Vector and scalar projections are defined in in the same way that they were defined for .
If x and y are vectors in , then
In the case that x and y are orthogonal, equation (4) becomes the Pythagorean law
The Pythagorean law is a generalization of the Pythagorean theorem. When x and y are nonzero orthogonal vectors in , we can use these vectors and their sum to form a right triangle as in Figure 5.1.4. The Pythagorean law relates the lengths of the sides of the triangle. Indeed, if we set
Figure 5.1.4.
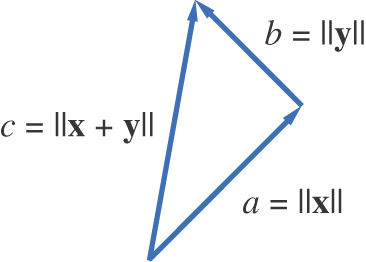
then
In many applications, the cosine of the angle between two nonzero vectors is used as a measure of how closely the directions of the vectors match up. If cos is near 1, then the angle between the vectors is small and hence the vectors are in nearly the same direction. A cosine value near zero would indicate that the angle between the vectors is nearly a right angle.
There are many other important applications involving angles between vectors. In particular, statisticians use the cosine of the angle between two vectors as a measure of how closely the two vectors are correlated.
