Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

6.8 Nonnegative Matrices

In many of the types of linear systems that occur in applications, the entries of the coefficient matrix represent nonnegative quantities. This section deals with the study of such matrices and some of their properties.

For an example of one of the applications of nonnegative matrices, we consider the Leontief input–output models.

Application 1 The Open Model

Suppose that there are n industries producing n different products. Each industry requires input of the products from the other industries and possibly even of its own product. In the open model, it is assumed that there is an additional demand for each of the products from an outside sector. The problem is to determine the output of each of the industries that is necessary to meet the total demand.

We will show that this problem can be represented by a linear system of equations and that the system has a unique nonnegative solution. Let $a_{ij}$ $a_{ij}$ denote the amount of input from the ith industry necessary to produce one unit of output in the jth industry. By a unit of input or output, we mean one dollar’s worth of the product. Thus, the total cost of producing one dollar’s worth of the jth product will be

a_{1 j} + a_{2 j} + \cdot \cdot \cdot + a_{nj}

$a_{1 j} + a_{2 j} + \cdot \cdot \cdot + a_{nj}$

Since the entries of A are all nonnegative, this sum is equal to ${| | a_{j} | |}_{1}$ ${| | a_{j} | |}_{1}$ . Clearly, production of the jth product will not be profitable unless ${| | a_{j} | |}_{1} < 1$ ${| | a_{j} | |}_{1} < 1$ . Let $d_{i}$ $d_{i}$ denote the demand of the open sector for the ith product. Finally, let $x_{i}$ $x_{i}$ represent the amount of output of the ith product necessary to meet the total demand. If the jth industry is to have an output of $x_{j}$ $x_{j}$ , it will need an input of $a_{ij} x_{j}$ $a_{ij} x_{j}$ units from the ith industry. Thus, the total demand for the ith product will be

a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n} + d_{i}

$a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n} + d_{i}$

and hence we require that

x_{i} = a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n} + d_{i}

$x_{i} = a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n} + d_{i}$

for $i = 1, . . ., n$ $i = 1, . . ., n$ . This leads to the system

\begin{matrix} (1 - a_{11}) x_{1} & + & (- a_{12}) x_{2} & + \cdot \cdot \cdot + & (- a_{1 n}) x_{n} & = & d_{1} \\ (- a_{21}) x_{1} & + & (1 - a_{22}) x_{2} & + \cdot \cdot \cdot + & (- a_{2 n}) x_{n} & = & d_{2} \\ ⋮ \\ (- a_{n 1}) x_{1} & + & (- a_{n 2}) x_{2} & + \cdot \cdot \cdot + & (1 - a_{nn}) x_{n} & = & d_{n} \end{matrix}

$\begin{matrix} (1 - a_{11}) x_{1} & + & (- a_{12}) x_{2} & + \cdot \cdot \cdot + & (- a_{1 n}) x_{n} & = & d_{1} \\ (- a_{21}) x_{1} & + & (1 - a_{22}) x_{2} & + \cdot \cdot \cdot + & (- a_{2 n}) x_{n} & = & d_{2} \\ ⋮ \\ (- a_{n 1}) x_{1} & + & (- a_{n 2}) x_{2} & + \cdot \cdot \cdot + & (1 - a_{nn}) x_{n} & = & d_{n} \end{matrix}$

which may be written in the form

(I - A) x = d

$(I - A) x = d$ (1)

The entries of A have two important properties:

$a_{ij} \geq 0$ $a_{ij} \geq 0$ for each i and j.
${| | a_{j} | |}_{1} = \sum_{i = 1}^{n} a_{ij} < 1$ ${| | a_{j} | |}_{1} = \sum_{i = 1}^{n} a_{ij} < 1$ for each j.

The vector x must not only be a solution of (1); it must also be nonnegative. (It would not make any sense to have a negative output.)

To show that the system has a unique nonnegative solution, we need to make use of a matrix norm that is related to the 1-norm for vectors that was introduced in Section 5.4. The matrix norm is also referred to as the 1-norm and is denoted by ${| | \cdot | |}_{1}$ ${| | \cdot | |}_{1}$ . The definition and properties of the 1-norm for matrices are studied in Section 7.4. In that section, we will show that, for any $m \times n$ $m \times n$ matrix B,

{| | B | |}_{1} = max_{1 \leq j \leq n} (\sum_{i = 1}^{m} | b_{ij} |) = max({| | b_{1} | |}_{1}, {| | b_{2} | |}_{1}, . . . , {| | b_{n} | |}_{1})

${| | B | |}_{1} = max_{1 \leq j \leq n} (\sum_{i = 1}^{m} | b_{ij} |) = max({| | b_{1} | |}_{1}, {| | b_{2} | |}_{1}, . . . , {| | b_{n} | |}_{1})$ (2)

It will also be shown that the 1-norm satisfies the following multiplicative properties:

\begin{matrix} {| | BC | |}_{1} \leq {| | B | |}_{1} {| | C | |}_{1} & \begin{matrix} for any matrix & C \in ℝ^{n \times r} \end{matrix} \\ {| | B x | |}_{1} \leq {| | B | |}_{1} {| | x | |}_{1} & \begin{matrix} \begin{matrix} for any \end{matrix} & x \in ℝ^{n} \end{matrix} \end{matrix}

$\begin{matrix} {| | BC | |}_{1} \leq {| | B | |}_{1} {| | C | |}_{1} & \begin{matrix} for any matrix & C \in ℝ^{n \times r} \end{matrix} \\ {| | B x | |}_{1} \leq {| | B | |}_{1} {| | x | |}_{1} & \begin{matrix} \begin{matrix} for any \end{matrix} & x \in ℝ^{n} \end{matrix} \end{matrix}$ (3)

In particular, if A is an $n \times n$ $n \times n$ matrix satisfying conditions (i) and (ii), then it follows from (2) that ${| | A | |}_{1} < 1$ ${| | A | |}_{1} < 1$ . Furthermore, if $λ$ $λ$ is any eigenvalue of A and x is an eigenvector belonging to $λ$ $λ$ , then

| λ | {| | x | |}_{1} = {| | λ x | |}_{1} = {| | A x | |}_{1} \leq {| | A | |}_{1} {| | x | |}_{1}

$| λ | {| | x | |}_{1} = {| | λ x | |}_{1} = {| | A x | |}_{1} \leq {| | A | |}_{1} {| | x | |}_{1}$

and hence

| λ | \leq {| | A | |}_{1} < 1

$| λ | \leq {| | A | |}_{1} < 1$

Thus, 1 is not an eigenvalue of A. It follows that $I - A$ $I - A$ is nonsingular and hence the system (1) has a unique solution

x = {(I - A)}^{- 1} d

$x = {(I - A)}^{- 1} d$

We would like to show that this solution must be nonnegative. To do this, we will show that ${(I - A)}^{- 1}$ ${(I - A)}^{- 1}$ is nonnegative. First note that, as a consequence of multiplicative property (3), we have

{| | A^{m} | |}_{1} \leq {| | A | |}_{1}^{m}

${| | A^{m} | |}_{1} \leq {| | A | |}_{1}^{m}$

Since ${| | A | |}_{1} < 1$ ${| | A | |}_{1} < 1$ , it follows that

\begin{matrix} \begin{matrix} {| | A^{m} | |}_{1} \to 0 & as \end{matrix} & m \to \infty \end{matrix}

$\begin{matrix} \begin{matrix} {| | A^{m} | |}_{1} \to 0 & as \end{matrix} & m \to \infty \end{matrix}$

and hence $A^{m}$ $A^{m}$ approaches the zero matrix as $m \to \infty$ $m \to \infty$ .

Since

(I - A) (I + A + \cdot \cdot \cdot + A^{m}) = I - A^{m + 1}

$(I - A) (I + A + \cdot \cdot \cdot + A^{m}) = I - A^{m + 1}$

it follows that

I + A + \cdot \cdot \cdot + A^{m} = {(I - A)}^{- 1} - {(I - A)}^{- 1} A^{m + 1}

$I + A + \cdot \cdot \cdot + A^{m} = {(I - A)}^{- 1} - {(I - A)}^{- 1} A^{m + 1}$

As $m \to \infty$ $m \to \infty$ ,

(I - A)^{- 1} - {(I - A)}^{- 1} A^{m + 1} \to {(I - A)}^{- 1}

$(I - A)^{- 1} - {(I - A)}^{- 1} A^{m + 1} \to {(I - A)}^{- 1}$

and hence the series $I + A + \cdot \cdot \cdot + A^{m}$ $I + A + \cdot \cdot \cdot + A^{m}$ converges to ${(I - A)}^{- 1}$ ${(I - A)}^{- 1}$ as $m \to \infty$ $m \to \infty$ . By condition (i), $I + A + \cdot \cdot \cdot + A^{m}$ $I + A + \cdot \cdot \cdot + A^{m}$ is nonnegative for each m, and therefore ${(I - A)}^{- 1}$ ${(I - A)}^{- 1}$ must be nonnegative. Since d is nonnegative, it follows that the solution x must be nonnegative. We see, then, that conditions (i) and (ii) guarantee that the system (1) will have a unique nonnegative solution x.

As you have probably guessed, there is also a closed version of the Leontief input– output model. In the closed version, it is assumed that each industry must produce enough output to meet the input needs of only the other industries and itself. The open sector is ignored. Thus, in place of the system (1), we have

(I - A) x = 0

$(I - A) x = 0$

and we require that x be a positive solution. The existence of such an x in this case is a much deeper result than in the open version and requires some more advanced theorems.

Theorem 6.8.1

Perron’s Theorem

If A is a positive $n \times n$ $n \times n$ matrix, then A has a positive real eigenvalue r with the following properties:

r is a simple root of the characteristic equation.
r has a positive eigenvector x.
If λ is any other eigenvalue of A, then $| λ | < r$ $| λ | < r$ .

The Perron theorem may be thought of as a special case of a more general theorem due to Frobenius. The Frobenius theorem applies to irreducible nonnegative matrices.

Example 1

Let A be a matrix of the form

[\begin{matrix} \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & 0 & 0 & \times \end{matrix}]

$[\begin{matrix} \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \\ \times & \times & 0 & 0 & \times \end{matrix}]$

Let $I_{1} = {1, 2, 5}$ $I_{1} = {1, 2, 5}$ and $I_{2} = {3, 4}$ $I_{2} = {3, 4}$ . Then $I_{1} \cup I_{2} = {1, 2, 3, 4, 5}$ $I_{1} \cup I_{2} = {1, 2, 3, 4, 5}$ and $a_{ij} = 0$ $a_{ij} = 0$ whenever $i \in I_{1}$ $i \in I_{1}$ and $j \in I_{2}$ $j \in I_{2}$ . Therefore, A is reducible. If P is the permutation matrix formed by interchanging the third and fifth rows of the identity matrix I, then

PA = [\begin{matrix} \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \end{matrix}]

$PA = [\begin{matrix} \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & 0 & 0 & \times \\ \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times \end{matrix}]$

and

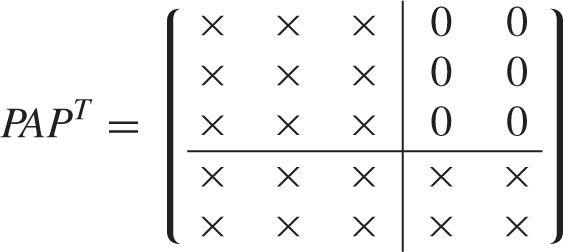
In general, it can be shown that an $n \times n$ $n \times n$ matrix A is reducible if and only if there exists a permutation matrix P such that ${PAP}^{T}$ ${PAP}^{T}$ is a matrix of the form

where B and C are square matrices.

∎

Theorem 6.8.2

Frobenius Theorem

If A is an irreducible nonnegative matrix, then A has a positive real eigenvalue r with the following properties:

r has a positive eigenvector x.
If λ is any other eigenvalue of A, then $| λ | \leq r$ $| λ | \leq r$ . The eigenvalues with absolute value equal to r are all simple roots of the characteristic equation. Indeed, if there are m eigenvalues with absolute value equal to r, they must be of the form

$\begin{matrix} \begin{matrix} λ_{k} & = {re}^{2 k π i / m} \end{matrix} & k = 0, 1, . . . , m - 1 \end{matrix}$ $\begin{matrix} \begin{matrix} λ_{k} & = {re}^{2 k π i / m} \end{matrix} & k = 0, 1, . . . , m - 1 \end{matrix}$

The proof of this theorem is beyond the scope of the text. We refer the reader to Gantmacher [4, Vol. 2]. Perron’s theorem follows as a special case of the Frobenius theorem.

Application 2 The Closed Model

In the closed Leontief input–output model, we assume that there is no demand from the open sector and we wish to find outputs to satisfy the demands of all n industries. Thus, defining the $x_{i} ’ s$ $x_{i} ’ s$ and the $a_{ij} ’ s$ $a_{ij} ’ s$ as in the open model, we have

x_{i} = a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n}

$x_{i} = a_{i 1} x_{1} + a_{i 2} x_{2} + \cdot \cdot \cdot + a_{in} x_{n}$

for $i = 1, . . . , n$ $i = 1, . . . , n$ . The resulting system may be written in the form

(A - I) x = 0

$(A - I) x = 0$ (4)

As before, we have the condition

a_{ij} \geq 0

$a_{ij} \geq 0$ (i)

Since there is no open sector, the amount of output from the jth industry should be the same as the total input for that industry. Thus,

x_{j} = \sum_{i = 1}^{n} a_{ij} x_{j}

$x_{j} = \sum_{i = 1}^{n} a_{ij} x_{j}$

and hence we have as our second condition

\begin{matrix} \sum_{i = 1}^{n} a_{ij} = 1 & j = 1, . . . , n \end{matrix}

$\begin{matrix} \sum_{i = 1}^{n} a_{ij} = 1 & j = 1, . . . , n \end{matrix}$ (ii)

Condition (ii) implies that $A - I$ $A - I$ is singular, because the sum of its row vectors is 0. Therefore, 1 is an eigenvalue of A, and since ${| | A | |}_{1} = 1$ ${| | A | |}_{1} = 1$ , it follows that all the eigenvalues of A have moduli less than or equal to 1. Let us assume that enough of the coefficients of A are nonzero so that A is irreducible. Then, by Theorem 6.8.2, $λ = 1$ $λ = 1$ has a positive eigenvector x. Thus, any positive multiple of x will be a positive solution of (4).

Application 3 Markov Chains Revisited

Nonnegative matrices also play an important role in the theory of Markov processes. Recall that if A is an $n \times n$ $n \times n$ stochastic matrix, then $λ_{1} = 1$ $λ_{1} = 1$ is an eigenvalue of A and the remaining eigenvalues satisfy

\begin{matrix} | λ_{j} | \leq 1 & for j = 2, . . . , n \end{matrix}

$\begin{matrix} | λ_{j} | \leq 1 & for j = 2, . . . , n \end{matrix}$

In the case that A is stochastic and all of its entries are positive, it follows from Perron’s theorem that $λ_{1} = 1$ $λ_{1} = 1$ must be a dominant eigenvalue and this, in turn, implies that the Markov chain with transition matrix A will converge to a steady-state vector for any starting probability vector $x_{0}$ $x_{0}$ . In fact, if, for some k, the matrix $A^{k}$ $A^{k}$ is positive, then by Perron’s theorem, $λ_{1} = 1$ $λ_{1} = 1$ must be a dominant eigenvalue of $A^{k}$ $A^{k}$ . One can then show that $λ_{1} = 1$ $λ_{1} = 1$ must also be a dominant eigenvalue of A. (See Exercise 12.) We say that a Markov process is regular if all of the entries of some power of the transition matrix are strictly positive. The transition matrix for a regular Markov process will have $λ_{1} = 1$ $λ_{1} = 1$ as a dominant eigenvalue, and hence the Markov chain is guaranteed to converge to a steady-state vector.

Application 4 Analytic Hierarchy Process: Eigenvector Computation of Weights

In Section 6.3, we considered an example involving a search process to fill a full professor position at a large university. In order to assign weights to the quality of the research of the four candidates, the committee did pairwise comparisons of the relative quality of the research publications of the candidates. After studying the publications of all the candidates, the committee agreed upon the following pairwise comparisons of the weights:

w_{1} = 1.75 w_{2}, w_{1} = 1.5 w_{3}, w_{1} = 1.25 w_{4}, w_{2} = 0.75 w_{3}, w_{2} = 0.50 w_{4}, w_{3} = 0.75 w_{4}

$w_{1} = 1.75 w_{2}, w_{1} = 1.5 w_{3}, w_{1} = 1.25 w_{4}, w_{2} = 0.75 w_{3}, w_{2} = 0.50 w_{4}, w_{3} = 0.75 w_{4}$

Here, an equation such as $w_{2} = 0.50 w_{4}$ $w_{2} = 0.50 w_{4}$ would indicate that the quality of research from candidate 2 was only half as strong as the quality of research from candidate 4. Equivalently, one could say that the quality of research from candidate 4 is twice as strong as the quality of research from candidate 2. In Chapter 5, we added the condition that the weights must all add up to 1. Using this condition, we were able to express $w_{4}$ $w_{4}$ in terms of $w_{1}, w_{2}$ $w_{1}, w_{2}$ , and $w_{3}$ $w_{3}$ . We then found the values of $w_{1}, w_{2}$ $w_{1}, w_{2}$ , and $w_{3}$ $w_{3}$ by calculating the least squares solution to a $6 \times 3$ $6 \times 3$ linear system. The calculated weight vector was $w_{1} = {(0.3289, 0.1739, 0.2188, 0.2784)}^{T}$ $w_{1} = {(0.3289, 0.1739, 0.2188, 0.2784)}^{T}$ .

We now consider an alternative method for computing the weight vector based on an eigenvector calculation. To do this, we first form a comparison matrix C. The $(i, j)$ $(i, j)$ entry of C indicates how the quality of the research of candidate i compares to the quality of the research of candidate j. Thus if, for example, $w_{2} = 0.5 w_{4}$ $w_{2} = 0.5 w_{4}$ , then $c_{24} = 2$ $c_{24} = 2$ and $c_{42} = \frac{1}{2}$ $c_{42} = \frac{1}{2}$ . The comparison matrix for judging the quality of research is given by

C = [\begin{matrix} 1 & \frac{7}{4} & \frac{3}{2} & \frac{5}{4} \\ \frac{4}{7} & 1 & \frac{3}{4} & \frac{1}{2} \\ \frac{2}{3} & \frac{4}{3} & 1 & \frac{3}{4} \\ \frac{4}{5} & 2 & \frac{4}{3} & 1 \end{matrix}]

$C = [\begin{matrix} 1 & \frac{7}{4} & \frac{3}{2} & \frac{5}{4} \\ \frac{4}{7} & 1 & \frac{3}{4} & \frac{1}{2} \\ \frac{2}{3} & \frac{4}{3} & 1 & \frac{3}{4} \\ \frac{4}{5} & 2 & \frac{4}{3} & 1 \end{matrix}]$

The matrix C is called a reciprocal matrix since it has the property that $c_{ji} = \frac{1}{c_{ij}}$ $c_{ji} = \frac{1}{c_{ij}}$ for all i and j. The matrix C is a positive matrix, so it follows by Perron’s theorem that C has a dominant eigenvalue with a positive eigenvector. The dominant eigenvalue is $λ_{1} = 4.0106$ $λ_{1} = 4.0106$ . If we compute the eigenvector belonging to $λ_{1}$ $λ_{1}$ and then normalize so that its entries add up to 1, we end up with a weight vector

w_{2} = {(0.3255, 0.1646, 0.2177, 0.2922)}^{T}

$w_{2} = {(0.3255, 0.1646, 0.2177, 0.2922)}^{T}$

The eigenvector solution $w_{2}$ $w_{2}$ is very close to the weight vector $w_{1}$ $w_{1}$ computed using least squares. Why does this eigenvector method work so well? To answer this question, let us first consider a simple example where both methods of computing weights give the exact same answer.

Suppose the mathematics department at a small college is conducting a search for an assistant professor position. Candidates will be evaluated in the areas of teaching, research, and professional activities. The committee decides that teaching is twice as important as research and 8 times as important as professional activities. The committee also decides that research is 4 times as important as professional activities. In this case, it is easy to find the weight vector since the decisions about the relative importance of the three areas were done in a consistent way.

If $w_{3}$ $w_{3}$ is the weight assigned to professional activities, then the weight for research $w_{2}$ $w_{2}$ must be $4 w_{3}$ $4 w_{3}$ and the weight $w_{1}$ $w_{1}$ must be $8 w_{3}$ $8 w_{3}$ . So $w_{1}$ $w_{1}$ is automatically equal to $2 w_{2}$ $2 w_{2}$ . The weight vector then must be of the form ${w = {(8 w_{3}, 4 w_{3}, w_{3})}^{}}^{T}$ ${w = {(8 w_{3}, 4 w_{3}, w_{3})}^{}}^{T}$ . In order for the entries of w to add up to 1, the value of $w_{3}$ $w_{3}$ must be $\frac{1}{13}$ $\frac{1}{13}$ . If we use the least squares method discussed in Section 6.3, we would set $w_{3} = 1 - w_{1} - w_{1}$ $w_{3} = 1 - w_{1} - w_{1}$ . The weight vector would then be computed by finding the least squares solution to a $3 \times 2$ $3 \times 2$ linear system. In this case, the $3 \times 2$ $3 \times 2$ system is consistent, so the least squares solution is the exact solution and our computed weight vector is $w = {(\frac{8}{13}, \frac{4}{13}, \frac{1}{13})}^{T}$ $w = {(\frac{8}{13}, \frac{4}{13}, \frac{1}{13})}^{T}$ .

Let us now compute the weight vector using the eigenvector method. To do this, we first form the comparison matrix

C = [\begin{matrix} 1 & 2 & 8 \\ \frac{1}{2} & 1 & 4 \\ \frac{1}{8} & \frac{1}{4} & 1 \end{matrix}]

$C = [\begin{matrix} 1 & 2 & 8 \\ \frac{1}{2} & 1 & 4 \\ \frac{1}{8} & \frac{1}{4} & 1 \end{matrix}]$

Note that $c_{12} = 2$ $c_{12} = 2$ since teaching is considered twice as important as professional activities and $c_{23} = 4$ $c_{23} = 4$ since research is considered 4 times as important as professional activities. Because the judgments of relative importance were made in a consistent manner, the value of $c_{13}$ $c_{13}$ , the relative importance of teaching to professional activities, should be

c_{13} = 2 \cdot 4 = c_{12} c_{23}

$c_{13} = 2 \cdot 4 = c_{12} c_{23}$

Indeed, if all decisions on the relative importance of the criteria are made in a consistent manner, then the entries of the comparison matrix will satisfy the property $c_{ij} = c_{ik} c_{kj}$ $c_{ij} = c_{ik} c_{kj}$ for all i, j, and k. A reciprocal comparison matrix with this property is said to be consistent. Note that the matrix C in our example has rank 1 since

\begin{matrix} c_{1} = \frac{1}{8} c_{3} & and & c_{2} \end{matrix} = \frac{1}{4} c_{3}

$\begin{matrix} c_{1} = \frac{1}{8} c_{3} & and & c_{2} \end{matrix} = \frac{1}{4} c_{3}$

In general, if C is an $n \times n$ $n \times n$ consistent reciprocal comparison matrix and $c_{j}$ $c_{j}$ and $c_{k}$ $c_{k}$ are column vectors of C, then

c_{j} = [\begin{matrix} \begin{matrix} \begin{matrix} c_{1 j} \\ c_{2 j} \end{matrix} \\ ⋮ \end{matrix} \\ c_{nj} \end{matrix}] = [\begin{matrix} \begin{matrix} \begin{matrix} c_{1 k} c_{kj} \\ c_{2 k} c_{kj} \end{matrix} \\ ⋮ \end{matrix} \\ c_{nk} c_{kj} \end{matrix}] = c_{kj} c_{k}

$c_{j} = [\begin{matrix} \begin{matrix} \begin{matrix} c_{1 j} \\ c_{2 j} \end{matrix} \\ ⋮ \end{matrix} \\ c_{nj} \end{matrix}] = [\begin{matrix} \begin{matrix} \begin{matrix} c_{1 k} c_{kj} \\ c_{2 k} c_{kj} \end{matrix} \\ ⋮ \end{matrix} \\ c_{nk} c_{kj} \end{matrix}] = c_{kj} c_{k}$

Therefore, C must have rank equal to 1. It follows that 0 must be an eigenvalue of C and the dimension of its eigenspace must be $n - 1$ $n - 1$ , the nullity of C. So 0 must be an eigenvalue of multiplicity $n - 1$ $n - 1$ . The remaining eigenvalue $λ_{1}$ $λ_{1}$ must equal the trace of C. So $λ_{1} = n$ $λ_{1} = n$ is the dominant eigenvalue of C. Furthermore, since C has rank 1, any column vector of C will be an eigenvector belonging to the dominant eigenvalue. (See Exercise 17 in Section 6.3.)

For our example, it follows that the dominant eigenvalue of C is $λ_{1} = 3$ $λ_{1} = 3$ and that $c_{3}$ $c_{3}$ is an eigenvector belonging to $λ_{1}$ $λ_{1}$ . If we divide $c_{3}$ $c_{3}$ by the sum of its entries, we end up with the weight vector $w = {(\frac{8}{13}, \frac{4}{13}, \frac{1}{13})}^{T}$ $w = {(\frac{8}{13}, \frac{4}{13}, \frac{1}{13})}^{T}$ .

In general, if the decisions on the relative importance are made in a consistent manner, then there is only one way to choose the weights and both the least squares method and the eigenvector method will produce the same weight vector. Suppose now that the decisions are not made in a consistent manner. This is not uncommon when decisions are made based on human judgments. For the least squares method, the linear system in the variables $w_{1}, w_{2}, . . ., w_{n - 1}$ $w_{1}, w_{2}, . . ., w_{n - 1}$ will not be consistent, but we can always find a least squares solution. If the eigenvector method is used, the comparison matrix $C_{1}$ $C_{1}$ will not be consistent. By Perron’s theorem, $C_{1}$ $C_{1}$ will have a positive dominant eigenvalue $λ_{1}$ $λ_{1}$ and a positive eigenvector $x_{1}$ $x_{1}$ . The eigenvector can be scaled to form a vector $w_{1}$ $w_{1}$ whose entries add to 1. The scaled vector $w_{1}$ $w_{1}$ is used to assign weights to the criteria. If the decisions on the relative importance have not been made in a wildly inconsistent manner, but in a way that is in some sense close to being consistent, then the eigenvector $w_{1}$ $w_{1}$ is a reasonable choice for a weight vector. In this case, the matrix $C_{1}$ $C_{1}$ should in some sense be close to a consistent reciprocal comparison matrix and $λ_{1}$ $λ_{1}$ and $w_{1}$ $w_{1}$ should be close to the dominant eigenvalue and eigenvector of a consistent matrix.

Suppose, for example, that the search committee at the college had decided, as before, that teaching is twice as important as research and 8 times as important as professional activities; however, suppose this time they decided that research should only be 3 times as important as professional activities. In this case, the comparison matrix is

C_{1} = [\begin{matrix} 1 & 2 & 8 \\ \frac{1}{2} & 1 & 3 \\ \frac{1}{8} & \frac{1}{3} & 1 \end{matrix}]

$C_{1} = [\begin{matrix} 1 & 2 & 8 \\ \frac{1}{2} & 1 & 3 \\ \frac{1}{8} & \frac{1}{3} & 1 \end{matrix}]$

The matrix C₁ is not consistent so its dominant eigenvalue $λ_{1} = 3.0092$ $λ_{1} = 3.0092$ is not equal to 3; however, it is close to 3. The eigenvector belonging to $λ_{1}$ $λ_{1}$ (normalized so that its entries add up to 1) is $w_{1} = {(0.6282, 0.2854, 0.864)}^{T}$ $w_{1} = {(0.6282, 0.2854, 0.864)}^{T}$ . Table 6.8.1 summarizes the results for both the problem with the consistent comparison matrix and for the inconsistent version of the problem. For each comparison matrix, the table includes the dominant eigenvalue and the computed weights. All computed values are rounded to four decimal places.

Table 6.8.1 A Comparison of Comparison Matrices

		Weights
Matrix	Eigenvalue	Teaching	Research	Prof. Activities
C	3	0.6154	0.3077	0.0769
$C_{1}$ $C_{1}$	3.0092	0.6282	0.2854	0.0864

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 6.8 Nonnegative Matrices

Create new playlist

Sign In

Sign Up

Table of Contents for
6.8 Nonnegative Matrices