Let us examine geometrically a system of the form

Each equation can be represented graphically as a line in the plane. The ordered pair $(x_1,x_2)$ will be a solution of the system if and only if it lies on both lines. For example, consider the three systems

1. 
   $\begin{array}{l}{x}_1+x_2=2\\ x_1-x_2=2\end{array}$

2. 
   $\begin{array}{l}{x}_1+x_2=2\\ x_1+x_2=1\end{array}$

3. 
   $\begin{array}{c}\phantom{-}{x}_1+x_2=\phantom{-}2\\ -x_1-x_2=-2\end{array}$

The two lines in system (i) intersect at the point (2, 0). Thus, {(2, 0)} is the solution set of (i). In system (ii), the two lines are parallel. Therefore, system (ii) is inconsistent and hence its solution set is empty. The two equations in system (iii) both represent the same line. Any point on this line will be a solution of the system (see Figure 1.1.1).

Figure 1.1.1.

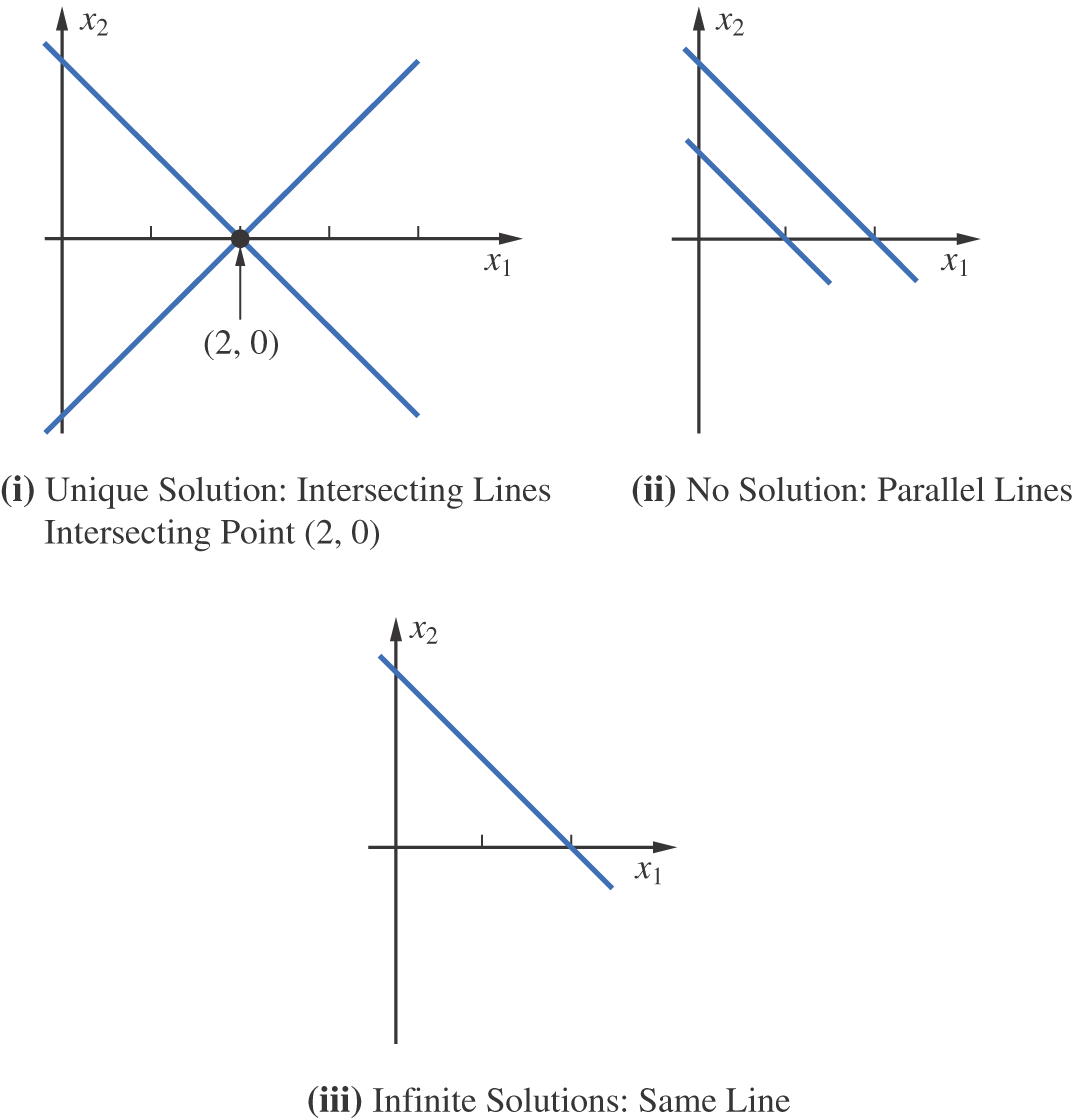
In general, there are three possibilities: the lines intersect at a point, they are parallel, or both equations represent the same line. The solution set then contains either one, zero, or infinitely many points.

The situation is the same for $m\times n$ systems. An $m\times n$ system may or may not be consistent. If it is consistent, it must have either exactly one solution or infinitely many solutions. These are the only possibilities. We will see why this is so in Section 1.2 when we study the row echelon form. Of more immediate concern is the problem of finding all solutions of a given system. To tackle this problem, we introduce the notion of equivalent systems.

Consider the two systems

1. 
   $\begin{array}{ccccc}\hfill 3x_1+2x_2& \hfill -& \hfill x_3& \hfill =& \hfill -2\\ \hfill x_2& \hfill & \hfill & \hfill =& \hfill 3\\ \hfill & \hfill & \hfill 2x_3& \hfill =& \hfill 4\end{array}$

2. 
   $\begin{array}{c}\hfill \phantom{-}3x_1+2x_2-x_3=-2\\ \hfill -3x_1-\phantom{2}{x}_2+x_3=\phantom{-}5\\ \hfill 3x_1+2x_2+x_3=\phantom{-}2\end{array}$

System (a) is easy to solve because it is clear from the last two equations that $x_2=3$ and $x_3=2$. Using these values in the first equation, we get

Thus, the solution of the system is $(\mathrm{-}\mathrm{2,\; 3,\; 2})$. System (b) seems to be more difficult to solve. Actually, system (b) has the same solution as system (a). To see this, add the first two equations of the system:

If $(x_1,x_2,x_3)$ is any solution of (b), it must satisfy all the equations of the system. Thus, it must satisfy any new equation formed by adding two of its equations. Therefore, $x_2$ must equal 3. Similarly, $(x_1,x_2,x_3)$ must satisfy the new equation formed by subtracting the first equation from the third:

Therefore, any solution of system (b) must also be a solution of system (a). By a similar argument, it can be shown that any solution of (a) is also a solution of (b). This can be done by subtracting the first equation from the second:

Then add the first and third equations:

Thus, $(x_1,x_2,x_3)$ is a solution of system (b) if and only if it is a solution of system (a). Therefore, both systems have the same solution set, $\left\{(-2,3,2)\right\}$.

If we interchange the order in which two equations of a system are written, this will have no effect on the solution set. The reordered system will be equivalent to the original system. For example, the systems

both involve the same three equations and, consequently, they must have the same solution set.

If one equation of a system is multiplied through by a nonzero real number, this will have no effect on the solution set, and the new system will be equivalent to the original system. For example, the systems

are equivalent.

If a multiple of one equation is added to another equation, the new system will be equivalent to the original system. This follows since the n-tuple $(x_1,\dots ,x_n)$ will satisfy the two equations

if and only if it satisfies the equations

To summarize, there are three operations that can be used on a system to obtain an equivalent system:

1. The order in which any two equations are written may be interchanged.

2. Both sides of an equation may be multiplied by the same nonzero real number.

3. A multiple of one equation may be added to (or subtracted from) another.

Given a system of equations, we may use these operations to obtain an equivalent system that is easier to solve.

Let us restrict ourselves to $n\times n$ systems for the remainder of this section. We will show that if an $n\times n$ system has exactly one solution, then operations I and III can be used to obtain an equivalent “strictly triangular system.”

Any $n\times n$ strictly triangular system can be solved in the same manner as the last example. First, the nth equation is solved for the value of $x_n$. This value is used in the $(n-1)$st equation to solve for $x_{n-1}$. The values $x_n$ and $x_{n-1}$ are used in the $(n-2)$nd equation to solve for $x_{n-2}$, and so on. We will refer to this method of solving a strictly triangular system as back substitution.

In general, given a system of n linear equations in n unknowns, we will use operations I and III to try to obtain an equivalent system that is strictly triangular. (We will see in the next section of the book that it is not possible to reduce the system to strictly triangular form in the cases where the system does not have a unique solution.)

Let us look back at the system of equations in the last example. We can associate with that system a $3\times 3$ array of numbers whose entries are the coefficients of the $x_i\text{’s}$:

We will refer to this array as the coefficient matrix of the system. The term matrix means a rectangular array of numbers. A matrix having m rows and n columns is said to be $m\times n$. A matrix is said to be square if it has the same number of rows and columns, that is, if $m=n$.

If we attach to the coefficient matrix an additional column whose entries are the numbers on the right-hand side of the system, we obtain the new matrix

We will refer to this new matrix as the augmented matrix. In general, when an $m\times r$ matrix B is attached to an $m\times n$ matrix A in this way, the augmented matrix is denoted by $\left(A\right|B)$. Thus, if

then

With each system of equations, we may associate an augmented matrix of the form

The system can be solved by performing operations on the augmented matrix. The $x_i\text{’s}$ are placeholders that can be omitted until the end of the computation. Corresponding to the three operations used to obtain equivalent systems, the following row operations may be applied to the augmented matrix:

Returning to the example, we find that the first row is used to eliminate the elements in the first column of the remaining rows. We refer to the first row as the pivotal row. For emphasis, the entries in the pivotal row are all in bold type and the entire row is color shaded. The first nonzero entry in the pivotal row is called the pivot.

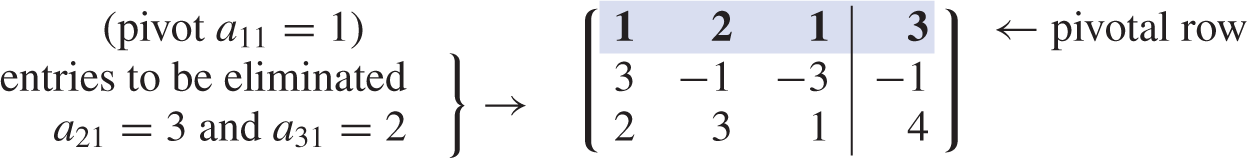
By using row operation III, 3 times the first row is subtracted from the second row and 2 times the first row is subtracted from the third. When this is done, we end up with the matrix

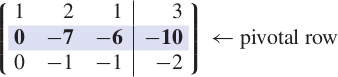
At this step, we choose the second row as our new pivotal row and apply row operation III to eliminate the last element in the second column. This time the pivot is $-7$ and the quotient $\frac{-1}{-7}=\frac{1}{7}$ is the multiple of the pivotal row that is subtracted from the third row. We end up with the matrix

This is the augmented matrix for the strictly triangular system, which is equivalent to the original system. The solution of the system is easily obtained by back substitution.

Example 4

Solve the system

$$\begin{array}{ccc}\hfill -x_2-x_3+x_4& =\hfill & \hfill 0\\ \hfill x_1+x_2+x_3+x_4& =\hfill & \hfill 6\\ \hfill 2x_1+4x_2+x_3-2x_4& =\hfill & \hfill -1\\ \hfill 3x_1+x_2-2x_3+2x_4& =\hfill & \hfill 3\end{array}$$

SOLUTION

The augmented matrix for this system is

$$\left[\begin{array}{cccc}0& \hfill -1& \hfill -1& \hfill 1\\ 1& \hfill 1& \hfill 1& \hfill 1\\ 2& \hfill 4& \hfill 1& \hfill -2\\ 3& \hfill 1& \hfill -2& \hfill 2\end{array}\right|\begin{array}{r}0\\ 6\\ -1\\ 3\end{array}]$$

Since it is not possible to eliminate any entries by using 0 as a pivot element, we will use row operation I to interchange the first two rows of the augmented matrix. The new first row will be the pivotal row and the pivot element will be 1:

1.1-3 Full Alternative Text

Row operation III is then used twice to eliminate the two nonzero entries in the first column:

1.1-4 Full Alternative Text

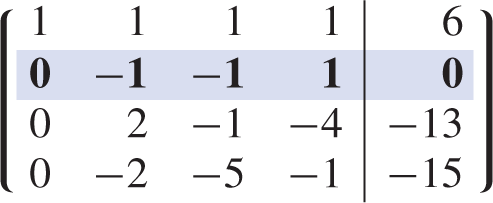
Next, the second row is used as the pivotal row to eliminate the entries in the second column below the pivot element $-1$:

1.1-5 Full Alternative Text

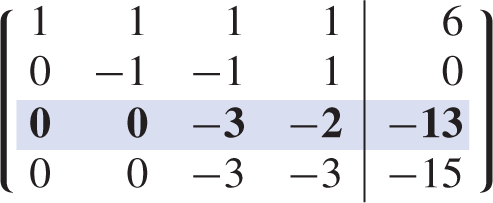
Finally, the third row is used as the pivotal row to eliminate the last element in the third column:

$$\left[\begin{array}{cccc}1& \hfill 1& \hfill 1& \hfill 1\\ 0& \hfill -1& \hfill -1& \hfill 1\\ 0& \hfill 0& \hfill -3& \hfill -2\\ 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right|\begin{array}{r}6\\ 0\\ -13\\ -2\end{array}]$$

This augmented matrix represents a strictly triangular system. Solving by back substitution, we obtain the solution $(\mathrm{2,} -\mathrm{1,}\mathrm{ 3,}\mathrm{ 2})$.

In general, if an $n\times n$ linear system can be reduced to strictly triangular form, then it will have a unique solution that can be obtained by performing back substitution on the triangular system. We can think of the reduction process as an algorithm involving $n-1$ steps. At the first step, a pivot element is chosen from among the nonzero entries in the first column of the matrix. The row containing the pivot element is called the pivotal row. We interchange rows (if necessary) so that the pivotal row is the new first row. Multiples of the pivotal row are then subtracted from each of the remaining $n-1$ rows so as to obtain 0’s in the first entries of rows 2 through n. At the second step, a pivot element is chosen from the nonzero entries in column 2, rows 2 through n, of the matrix. The row containing the pivot is then interchanged with the second row of the matrix and is used as the new pivotal row. Multiples of the pivotal row are then subtracted from the remaining $n-2$ rows so as to eliminate all entries below the pivot in the second column. The same procedure is repeated for columns 3 through $n-1$. Note that at the second step row 1 and column 1 remain unchanged, at the third step the first two rows and first two columns remain unchanged, and so on. At each step, the overall dimensions of the system are effectively reduced by 1 (see Figure 1.1.2).

Figure 1.1.2.

If the elimination process can be carried out as described, we will arrive at an equivalent strictly triangular system after $n-1$ steps. However, the procedure will break down if, at any step, all possible choices for a pivot element are equal to 0. When this happens, the alternative is to reduce the system to certain special echelon, or staircase-shaped, forms. These echelon forms will be studied in the next section. They will also be used for $m\times n$ systems, where $m\ne n$.