Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5.4 Inner Product Spaces

Scalar products are useful not only in $ℝ^{n}$ $ℝ^{n}$ , but also in a wide variety of contexts. To generalize this concept to other vector spaces, we introduce the following definition.

Definition and Examples

A vector space V with an inner product is called an inner product space.

The Vector Space $ℝ^{n}$ $ℝ^{n}$

The standard inner product for $ℝ^{n}$ $ℝ^{n}$ is the scalar product

〈 x, y 〉 = x^{T} y

$〈 x, y 〉 = x^{T} y$

Given a vector w with positive entries, we could also define an inner product on $ℝ^{n}$ $ℝ^{n}$ by

〈 x, y 〉 = \sum_{i = 1}^{n} x_{i} y_{i} w_{i}

$〈 x, y 〉 = \sum_{i = 1}^{n} x_{i} y_{i} w_{i}$ (1)

The entries $w_{i}$ $w_{i}$ are referred to as weights.

The Vector Space $ℝ^{m \times n}$ $ℝ^{m \times n}$

Given A and B in $ℝ^{m \times n}$ $ℝ^{m \times n}$ , we can define an inner product by

〈 A, B 〉 = \sum_{i = 1}^{m} \sum_{j = 1}^{n} a_{i j} b_{i j}

$〈 A, B 〉 = \sum_{i = 1}^{m} \sum_{j = 1}^{n} a_{i j} b_{i j}$

We leave it to the reader to verify that (2) does indeed define an inner product on $ℝ^{m \times n}$ $ℝ^{m \times n}$ .

The Vector Space C[a, b]

We may define an inner product on C[a, b] by

〈 f, g 〉 = \int_{a}^{b} f (x) g (x) d x

$〈 f, g 〉 = \int_{a}^{b} f (x) g (x) d x$ (3)

Note that

〈 f, f 〉 = \int_{a}^{b} {(f (x))}^{2} d x \geq 0

$〈 f, f 〉 = \int_{a}^{b} {(f (x))}^{2} d x \geq 0$

If $f (x_{0}) \neq 0$ $f (x_{0}) \neq 0$ for some $x_{0}$ $x_{0}$ in [a, b], then, since ${(f (x))}^{2}$ ${(f (x))}^{2}$ is continuous, there exists a subinterval I of [a, b] containing $x_{0}$ $x_{0}$ such that ${(f (x))}^{2} \geq {(f (x_{0}))}^{2} / 2$ ${(f (x))}^{2} \geq {(f (x_{0}))}^{2} / 2$ for all x in I. If we let p represent the length of I, then it follows that

〈 f, f 〉 = \int_{a}^{b} {(f (x))}^{2} d x \geq \int_{I} {(f (x))}^{2} d x \geq \frac{{(f (x_{0}))}^{2} P}{2} > 0

$〈 f, f 〉 = \int_{a}^{b} {(f (x))}^{2} d x \geq \int_{I} {(f (x))}^{2} d x \geq \frac{{(f (x_{0}))}^{2} P}{2} > 0$

So if $〈 f, f 〉 = 0$ $〈 f, f 〉 = 0$ , then f (x) must be identically zero on [a, b]. We leave it to the reader to verify that (3) satisfies the other two conditions specified in the definition of an inner product.

If w(x) is a positive continuous function on [a, b], then

〈 f, g 〉 = \int_{a}^{b} f (x) g (x) w (x) d x

$〈 f, g 〉 = \int_{a}^{b} f (x) g (x) w (x) d x$ (4)

also defines an inner product on C[a, b]. The function w(x) is called a weight function. Thus, it is possible to define many different inner products on C[a, b].

The Vector Space $P_{n}$ $P_{n}$

Let $x_{1}, x_{2}, …, x_{n}$ $x_{1}, x_{2}, …, x_{n}$ be distinct real numbers. For each pair of polynomials in $P_{n}$ $P_{n}$ , define

〈 p, q 〉 = \sum_{i = 1}^{n} P (x_{i}) g (x_{i})

$〈 p, q 〉 = \sum_{i = 1}^{n} P (x_{i}) g (x_{i})$ (5)

It is easily seen that (5) satisfies conditions (ii) and (iii) of the definition of an inner product. To show that (i) holds, note that

〈 p, p 〉 = \sum_{i = 1}^{n} {(p (x_{i}))}^{2} \geq 0

$〈 p, p 〉 = \sum_{i = 1}^{n} {(p (x_{i}))}^{2} \geq 0$

If $〈 p, p 〉 = 0$ $〈 p, p 〉 = 0$ , then $x_{1}, x_{2}, …, x_{n}$ $x_{1}, x_{2}, …, x_{n}$ must be roots of $p (x) = 0$ $p (x) = 0$ . Since p(x) is of degree less than n, it must be the zero polynomial.

If w(x) is a positive function, then

〈 p, q 〉 = \sum_{i = 1}^{n} P (x_{i}) q (x_{i}) w (x_{i})

$〈 p, q 〉 = \sum_{i = 1}^{n} P (x_{i}) q (x_{i}) w (x_{i})$

also defines an inner product on $P_{n}$ $P_{n}$ .

Basic Properties of Inner Product Spaces

The results presented in Section 5.1 for scalar products in $ℝ^{n}$ $ℝ^{n}$ all generalize to inner product spaces. In particular, if v is a vector in an inner product space V, the length, or norm of v is given by

‖ v ‖ = \sqrt{〈 v, v 〉}

$‖ v ‖ = \sqrt{〈 v, v 〉}$

Two vectors u and v are said to be orthogonal if $〈 u, v 〉 = 0$ $〈 u, v 〉 = 0$ . As in $ℝ^{n}$ $ℝ^{n}$ , a pair of orthogonal vectors will satisfy the Pythagorean law.

Theorem 5.4.1 The Pythagorean Law

If u and v are orthogonal vectors in an inner product space V, then

{‖ u + v ‖}^{2} = {‖ u ‖}^{2} + {‖ v ‖}^{2}

${‖ u + v ‖}^{2} = {‖ u ‖}^{2} + {‖ v ‖}^{2}$

Proof

\begin{matrix} {‖ u + v ‖}^{2} & = 〈 u + v, u + v 〉 \\ = 〈 u, u 〉 + 2 〈 u, v 〉 + 〈 v, v 〉 \\ = {‖ u ‖}^{2} + {‖ v ‖}^{2} \end{matrix}

$\begin{matrix} {‖ u + v ‖}^{2} & = 〈 u + v, u + v 〉 \\ = 〈 u, u 〉 + 2 〈 u, v 〉 + 〈 v, v 〉 \\ = {‖ u ‖}^{2} + {‖ v ‖}^{2} \end{matrix}$

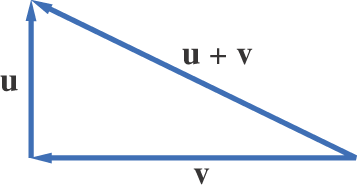
Interpreted in $ℝ^{2}$ $ℝ^{2}$ , this is just the familiar Pythagorean theorem as shown in Figure 5.4.1.

Three vectors represent Pythagorean theorem.

Figure 5.4.1. Full Alternative Text

Example 1

Consider the vector space $C [- 1, 1]$ $C [- 1, 1]$ with an inner product defined by (3). The vectors 1 and x are orthogonal, since

〈 1, x 〉 = \int_{- 1}^{1} 1 \cdot x d x = 0

$〈 1, x 〉 = \int_{- 1}^{1} 1 \cdot x d x = 0$

To determine the lengths of these vectors, we compute

\begin{matrix} 〈 1, 1 〉 & = \int_{- 1}^{1} 1 \cdot 1 d x = 2 \\ 〈 x, x 〉 & = \int_{- 1}^{1} x^{2} d x = \frac{2}{3} \end{matrix}

$\begin{matrix} 〈 1, 1 〉 & = \int_{- 1}^{1} 1 \cdot 1 d x = 2 \\ 〈 x, x 〉 & = \int_{- 1}^{1} x^{2} d x = \frac{2}{3} \end{matrix}$

It follows that

\begin{matrix} ‖ 1 ‖ & = {(〈 1, 1 〉)}^{1 / 2} = \sqrt{2} \\ ‖ x ‖ & = {(〈 x, x 〉)}^{1 / 2} = \frac{\sqrt{6}}{3} \end{matrix}

$\begin{matrix} ‖ 1 ‖ & = {(〈 1, 1 〉)}^{1 / 2} = \sqrt{2} \\ ‖ x ‖ & = {(〈 x, x 〉)}^{1 / 2} = \frac{\sqrt{6}}{3} \end{matrix}$

Since 1 and x are orthogonal, they satisfy the Pythagorean law:

{\begin{matrix} ‖ 1 + x ‖ \end{matrix}}^{2} = {\begin{matrix} ‖ 1 ‖ \end{matrix}}^{2} + {\begin{matrix} ‖ x ‖ \end{matrix}}^{2} = 2 + \frac{2}{3} = \frac{8}{3}

${\begin{matrix} ‖ 1 + x ‖ \end{matrix}}^{2} = {\begin{matrix} ‖ 1 ‖ \end{matrix}}^{2} + {\begin{matrix} ‖ x ‖ \end{matrix}}^{2} = 2 + \frac{2}{3} = \frac{8}{3}$

The reader may verify that

{\begin{matrix} ‖ 1 + x ‖ \end{matrix}}^{2} = 〈 1 + x, 1 + x 〉 = \int_{- 1}^{1} {(1 + x)}^{2} d x = \frac{8}{3}

${\begin{matrix} ‖ 1 + x ‖ \end{matrix}}^{2} = 〈 1 + x, 1 + x 〉 = \int_{- 1}^{1} {(1 + x)}^{2} d x = \frac{8}{3}$

Example 2

For the vector space $C [- π, π]$ $C [- π, π]$ , if we use a constant weight function $w (x) = 1 / π$ $w (x) = 1 / π$ to define an inner product

〈 f, g 〉 = \frac{1}{π} \int_{- π}^{π} f (x) g (x) d x

$〈 f, g 〉 = \frac{1}{π} \int_{- π}^{π} f (x) g (x) d x$ (6)

then

\begin{matrix} 〈 \cos x, \sin x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \cos x \sin x d x = 0 \end{matrix} \\ 〈 \cos x, \cos x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \cos x \cos x d x = 1 \end{matrix} \\ 〈 \sin x, \sin x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \sin x \sin x d x = 1 \end{matrix} \end{matrix}

$\begin{matrix} 〈 \cos x, \sin x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \cos x \sin x d x = 0 \end{matrix} \\ 〈 \cos x, \cos x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \cos x \cos x d x = 1 \end{matrix} \\ 〈 \sin x, \sin x 〉 & \begin{matrix} \begin{matrix} = \end{matrix} & \frac{1}{π} \int_{- π}^{π} \sin x \sin x d x = 1 \end{matrix} \end{matrix}$

Thus, cos x and sin x are orthogonal unit vectors with respect to this inner product. It follows from the Pythagorean law that

‖ \cos x + \sin x ‖ = \sqrt{2}

$‖ \cos x + \sin x ‖ = \sqrt{2}$

The inner product (6) plays a key role in Fourier analysis applications involving a trigonometric approximation of functions. We will look at some of these applications in Section 5.5.

For the vector space $ℝ^{m \times n}$ $ℝ^{m \times n}$ , the norm derived from the inner product (2) is called the Frobenius norm and is denoted by ${‖ \cdot ‖}_{F}$ ${‖ \cdot ‖}_{F}$ . Thus, if $A \in ℝ^{m \times n}$ $A \in ℝ^{m \times n}$ , then

{‖ A ‖}_{F} = {(〈 A, A 〉)}^{1 / 2} = {(\sum_{i = 1}^{m} \sum_{j = 1}^{n} a_{i j}^{2})}^{1 / 2}

${‖ A ‖}_{F} = {(〈 A, A 〉)}^{1 / 2} = {(\sum_{i = 1}^{m} \sum_{j = 1}^{n} a_{i j}^{2})}^{1 / 2}$

Example 3

\begin{matrix} A = [\begin{matrix} 1 & 1 \\ 1 & 2 \\ 3 & 3 \end{matrix}] & \begin{matrix} and & B = [\begin{matrix} - 1 & 1 \\ 3 & 0 \\ - 3 & 4 \end{matrix}] \end{matrix} \end{matrix}

$\begin{matrix} A = [\begin{matrix} 1 & 1 \\ 1 & 2 \\ 3 & 3 \end{matrix}] & \begin{matrix} and & B = [\begin{matrix} - 1 & 1 \\ 3 & 0 \\ - 3 & 4 \end{matrix}] \end{matrix} \end{matrix}$

then

〈 A, B 〉 = 1 \cdot - 1 + 1 \cdot 1 + 1 \cdot 3 + 2 \cdot 0 + 3 \cdot - 3 + 3 \cdot 4 = 6

$〈 A, B 〉 = 1 \cdot - 1 + 1 \cdot 1 + 1 \cdot 3 + 2 \cdot 0 + 3 \cdot - 3 + 3 \cdot 4 = 6$

Hence, A is not orthogonal to B. The norms of these matrices are given by

\begin{matrix} {‖ A ‖}_{F} & = {(1 + 1 + 1 + 1 + 9 + 9)}^{1 / 2} = 5 \\ {‖ B ‖}_{F} & = {(1 + 1 + 9 + 0 + 9 + 16)}^{1 / 2} = 6 \end{matrix}

$\begin{matrix} {‖ A ‖}_{F} & = {(1 + 1 + 1 + 1 + 9 + 9)}^{1 / 2} = 5 \\ {‖ B ‖}_{F} & = {(1 + 1 + 9 + 0 + 9 + 16)}^{1 / 2} = 6 \end{matrix}$

Example 4

In $P_{5}$ $P_{5}$ , define an inner product by (5) with $x_{i} = (i - 1) / 4$ $x_{i} = (i - 1) / 4$ for $i = 1, 2, …, 5$ $i = 1, 2, …, 5$ . The length of the function $P (x) = 4 x$ $P (x) = 4 x$ is given by

‖ 4 x ‖ = {(〈 4 x, 4 x 〉)}^{1 / 2} = {(\sum_{i = 1}^{5} 16 x_{i}^{2})}^{1 / 2} = {(\sum_{i = 1}^{5} {(i - 1)}^{2})}^{1 / 2} = \sqrt{30}

$‖ 4 x ‖ = {(〈 4 x, 4 x 〉)}^{1 / 2} = {(\sum_{i = 1}^{5} 16 x_{i}^{2})}^{1 / 2} = {(\sum_{i = 1}^{5} {(i - 1)}^{2})}^{1 / 2} = \sqrt{30}$

Observations

If $v \neq 0$ $v \neq 0$ and p is the vector projection of u onto v, then

$u - p$ $u - p$ and p are orthogonal.
$u = p$ $u = p$ if and only if u is a scalar multiple of v.

Proof of Observation I

Since

〈 p, p 〉 = 〈 \frac{α}{‖ v ‖} v, \frac{α}{‖ v ‖} v 〉 = {(\frac{α}{‖ v ‖})}^{2} 〈 v, v 〉 = α^{2}

$〈 p, p 〉 = 〈 \frac{α}{‖ v ‖} v, \frac{α}{‖ v ‖} v 〉 = {(\frac{α}{‖ v ‖})}^{2} 〈 v, v 〉 = α^{2}$

and

〈 u, p 〉 = \frac{(〈 u, v 〉)^{2}}{〈 v, v 〉} = α^{2}

$〈 u, p 〉 = \frac{(〈 u, v 〉)^{2}}{〈 v, v 〉} = α^{2}$

it follows that

〈 u - p, p 〉 = 〈 u, p 〉 - 〈 p, p 〉 = α^{2} - α^{2} = 0

$〈 u - p, p 〉 = 〈 u, p 〉 - 〈 p, p 〉 = α^{2} - α^{2} = 0$

Therefore, $u - p$ $u - p$ and p are orthogonal.

∎

Proof of Observation II

If $u = β v$ $u = β v$ , then the vector projection of u onto v is given by

p = \frac{〈 β v, v 〉}{〈 v, v 〉} v = β v = u

$p = \frac{〈 β v, v 〉}{〈 v, v 〉} v = β v = u$

Conversely, if $u = p$ $u = p$ , it follows from (7) that

\begin{matrix} u = β v & \begin{matrix} where & β = \frac{α}{‖ v ‖} \end{matrix} \end{matrix}

$\begin{matrix} u = β v & \begin{matrix} where & β = \frac{α}{‖ v ‖} \end{matrix} \end{matrix}$

∎

Observations I and II are useful for establishing the following theorem.

Theorem 5.4.2 The Cauchy—Schwarz Inequality

If u and v are any two vectors in an inner product space V, then

| 〈 u, v 〉 | \leq ‖ u ‖ ‖ v ‖

$| 〈 u, v 〉 | \leq ‖ u ‖ ‖ v ‖$ (8)

Equality holds if and only if u and v are linearly dependent.

Proof

If $v = 0$ $v = 0$ , then

| 〈 u, v 〉 | = 0 = ‖ u ‖ ‖ v ‖

$| 〈 u, v 〉 | = 0 = ‖ u ‖ ‖ v ‖$

If $v \neq 0$ $v \neq 0$ , then let p be the vector projection of u onto v. Since p is orthogonal to $u - p$ $u - p$ , it follows from the Pythagorean law that

{‖ p ‖}^{2} + {‖ u - p ‖}^{2} = {‖ u ‖}^{2}

${‖ p ‖}^{2} + {‖ u - p ‖}^{2} = {‖ u ‖}^{2}$

Thus,

\frac{(〈 u, v 〉)^{2}}{{‖ v ‖}^{2}} = {‖ p ‖}^{2} = {‖ u ‖}^{2} - {‖ u - p ‖}^{2}

$\frac{(〈 u, v 〉)^{2}}{{‖ v ‖}^{2}} = {‖ p ‖}^{2} = {‖ u ‖}^{2} - {‖ u - p ‖}^{2}$

and hence

(〈 u, v 〉)^{2} = {‖ u ‖}^{2} {‖ v ‖}^{2} - {‖ u - p ‖}^{2} {‖ v ‖}^{2} \leq {‖ u ‖}^{2} {‖ v ‖}^{2}

$(〈 u, v 〉)^{2} = {‖ u ‖}^{2} {‖ v ‖}^{2} - {‖ u - p ‖}^{2} {‖ v ‖}^{2} \leq {‖ u ‖}^{2} {‖ v ‖}^{2}$

Therefore,

| 〈 u, v 〉 | \leq ‖ u ‖ ‖ v ‖

$| 〈 u, v 〉 | \leq ‖ u ‖ ‖ v ‖$

Equality holds in (9) if and only if $u = p$ $u = p$ . It follows from observation II that equality will hold in (8) if and only if $v = p$ $v = p$ or u is a multiple of v. More simply stated, equality will hold if and only if u and v are linearly dependent.

One consequence of the Cauchy–Schwarz inequality is that if u and v are nonzero vectors, then

- 1 \leq \frac{〈 u, v 〉}{‖ u ‖ ‖ v ‖} \leq 1

$- 1 \leq \frac{〈 u, v 〉}{‖ u ‖ ‖ v ‖} \leq 1$

and hence there is a unique angle $θ$ $θ$ in [0, π] such that

\cos θ = \frac{〈 u, v 〉}{‖ u ‖ ‖ v ‖}

$\cos θ = \frac{〈 u, v 〉}{‖ u ‖ ‖ v ‖}$ (10)

Thus, equation (10) can be used to define the angle $θ$ $θ$ between two nonzero vectors u and v.

Norms

The word norm in mathematics has its own meaning that is independent of an inner product and its use here should be justified.

The third condition is called the triangle inequality (see Figure 5.4.2).

Figure 5.4.2. Full Alternative Text

Theorem 5.4.3

If V is an inner product space, then the equation

\begin{matrix} ‖ v ‖ = \sqrt{〈 v, v 〉} & \begin{matrix} \begin{matrix} for all \end{matrix} & v \in V \end{matrix} \end{matrix}

$\begin{matrix} ‖ v ‖ = \sqrt{〈 v, v 〉} & \begin{matrix} \begin{matrix} for all \end{matrix} & v \in V \end{matrix} \end{matrix}$

defines a norm on V.

Proof

It is easily seen that conditions I and II of the definition are satisfied. We leave this for the reader to verify and proceed to show that condition III is satisfied.

\begin{matrix} ‖ u + v ‖^{2} & = 〈 u + v, u + v 〉 \\ = 〈 u, u 〉 + 2 〈 u, v 〉 + 〈 v, v 〉 \\ \leq {‖ u ‖}^{2} + 2 ‖ u ‖ ‖ v ‖ + ‖ v ‖^{2} & (Cauchy - Schwarz) \\ = (‖ u ‖ + ‖ v ‖)^{2} \end{matrix}

$\begin{matrix} ‖ u + v ‖^{2} & = 〈 u + v, u + v 〉 \\ = 〈 u, u 〉 + 2 〈 u, v 〉 + 〈 v, v 〉 \\ \leq {‖ u ‖}^{2} + 2 ‖ u ‖ ‖ v ‖ + ‖ v ‖^{2} & (Cauchy - Schwarz) \\ = (‖ u ‖ + ‖ v ‖)^{2} \end{matrix}$

Thus,

‖ u + v ‖ \leq ‖ u ‖ + ‖ v ‖

$‖ u + v ‖ \leq ‖ u ‖ + ‖ v ‖$

∎

It is possible to define many different norms on a given vector space. For example, in $ℝ^{n}$ $ℝ^{n}$ we could define

{‖ x ‖}_{1} = \sum_{i = 1}^{n} | x_{i} |

${‖ x ‖}_{1} = \sum_{i = 1}^{n} | x_{i} |$

for every $x = {(x_{1}, x_{2}, …, x_{n})}^{T}$ $x = {(x_{1}, x_{2}, …, x_{n})}^{T}$ . It is easily verified that ${‖ \cdot ‖}_{1}$ ${‖ \cdot ‖}_{1}$ defines a norm on $ℝ^{n}$ $ℝ^{n}$ . Another important norm on $ℝ^{n}$ $ℝ^{n}$ is the uniform norm or infinity norm, which is defined by

{‖ x ‖}_{\infty} = max_{1 \leq i \leq n} | x_{i} |

${‖ x ‖}_{\infty} = max_{1 \leq i \leq n} | x_{i} |$

More generally, we could define a norm on $ℝ^{n}$ $ℝ^{n}$ by

{‖ x ‖}_{p} = {(\sum_{i = 1}^{n} | x_{i} |^{p})}^{1 / p}

${‖ x ‖}_{p} = {(\sum_{i = 1}^{n} | x_{i} |^{p})}^{1 / p}$

for any real number $p \geq 1$ $p \geq 1$ . In particular, if $p = 2$ $p = 2$ , then

{‖ x ‖}_{2} = {(\sum_{i = 1}^{n} | x_{i} |^{2})}^{1 / 2} = \sqrt{〈 x, x 〉}

${‖ x ‖}_{2} = {(\sum_{i = 1}^{n} | x_{i} |^{2})}^{1 / 2} = \sqrt{〈 x, x 〉}$

The norm ${‖ \cdot ‖}_{2}$ ${‖ \cdot ‖}_{2}$ is the norm on $ℝ^{n}$ $ℝ^{n}$ derived from the inner product. If $p \neq 2, {‖ \cdot ‖}_{p}$ $p \neq 2, {‖ \cdot ‖}_{p}$ does not correspond to any inner product. In the case of a norm that is not derived from an inner product, the Pythagorean law will not hold. For example,

\begin{matrix} x_{1} = [\begin{matrix} 1 \\ 2 \end{matrix}] & \begin{matrix} and & x_{2} = [\begin{matrix} - 4 \\ 2 \end{matrix}] \end{matrix} \end{matrix}

$\begin{matrix} x_{1} = [\begin{matrix} 1 \\ 2 \end{matrix}] & \begin{matrix} and & x_{2} = [\begin{matrix} - 4 \\ 2 \end{matrix}] \end{matrix} \end{matrix}$

are orthogonal; however,

{‖ x_{1} ‖}_{\infty}^{2} + {‖ x_{2} ‖}_{\infty}^{2} = 4 + 16 = 20

${‖ x_{1} ‖}_{\infty}^{2} + {‖ x_{2} ‖}_{\infty}^{2} = 4 + 16 = 20$

while

{‖ x_{1} + x_{2} ‖}_{\infty}^{2} = 16

${‖ x_{1} + x_{2} ‖}_{\infty}^{2} = 16$

If, however, ${‖ \cdot ‖}_{2}$ ${‖ \cdot ‖}_{2}$ is used, then

{‖ x_{1} ‖}_{2}^{2} + {‖ x_{2} ‖}_{2}^{2} = 5 + 20 = 25 = {‖ x_{1} + x_{2} ‖}_{2}^{2}

${‖ x_{1} ‖}_{2}^{2} + {‖ x_{2} ‖}_{2}^{2} = 5 + 20 = 25 = {‖ x_{1} + x_{2} ‖}_{2}^{2}$

Example 5

Let x be the vector ${(4, - 5, 3)}^{T}$ ${(4, - 5, 3)}^{T}$ in $ℝ^{3}$ $ℝ^{3}$ . Compute ${‖ x ‖}_{1}, {‖ x ‖}_{2}$ ${‖ x ‖}_{1}, {‖ x ‖}_{2}$ , and ${‖ x ‖}_{\infty}$ ${‖ x ‖}_{\infty}$ .

\begin{matrix} ‖ x ‖_{1} & \begin{matrix} \begin{matrix} = \end{matrix} & | 4 | + | - 5 | + | 3 | = 12 \end{matrix} \\ ‖ x ‖_{2} & \begin{matrix} \begin{matrix} = \end{matrix} & \sqrt{\begin{matrix} 16 + 25 + 9 \end{matrix}} = 5 \sqrt{2} \end{matrix} \\ ‖ x ‖_{\infty} & \begin{matrix} \begin{matrix} = \end{matrix} & max (| 4 |, | - 5 |, | 3 |) = 5 \end{matrix} \end{matrix}

$\begin{matrix} ‖ x ‖_{1} & \begin{matrix} \begin{matrix} = \end{matrix} & | 4 | + | - 5 | + | 3 | = 12 \end{matrix} \\ ‖ x ‖_{2} & \begin{matrix} \begin{matrix} = \end{matrix} & \sqrt{\begin{matrix} 16 + 25 + 9 \end{matrix}} = 5 \sqrt{2} \end{matrix} \\ ‖ x ‖_{\infty} & \begin{matrix} \begin{matrix} = \end{matrix} & max (| 4 |, | - 5 |, | 3 |) = 5 \end{matrix} \end{matrix}$

It is also possible to define different matrix norms for $ℝ^{m \times n}$ $ℝ^{m \times n}$ . In Chapter 7, we will study other types of matrix norms that are useful in determining the sensitivity of linear systems.

In general, a norm provides a way of measuring the distance between vectors.

Many applications involve finding a unique closest vector in a subspace S to a given vector v in a vector space V. If the norm used for V is derived from an inner product, then the closest vector can be computed as a vector projection of v onto the subspace S. This type of approximation problem is discussed further in the next section.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 5.4 Inner Product Spaces

Create new playlist

Sign In

Sign Up

Table of Contents for
5.4 Inner Product Spaces