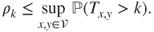1.4.4.3 Some computations on particle distribution
At equilibrium, that is, under the invariant law, the ![]() are uniform on
are uniform on ![]() and hence, the
and hence, the ![]() for
for ![]() are i.i.d. uniform on
are i.i.d. uniform on ![]() . The strong law of large numbers and the central limit theorem then yield that
. The strong law of large numbers and the central limit theorem then yield that
Hence, as ![]() goes to infinity, the instantaneous proportion of molecules in each compartment converges to
goes to infinity, the instantaneous proportion of molecules in each compartment converges to ![]() with fluctuations of order
with fluctuations of order ![]() . For instance,
. For instance,
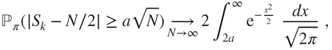
and as a numerical illustration, as ![]() , the choice
, the choice ![]() and
and ![]() yields that
yields that ![]() and hence
and hence
For an arbitrary initial law, for ![]() and
and ![]() ,
,
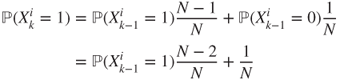
and the solution of this affine recursion, with fixed point ![]() , is given by
, is given by
Then, at geometric rate,
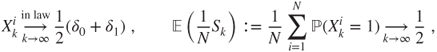
The rate ![]() seems poor, but the time unit should actually be of order
seems poor, but the time unit should actually be of order ![]() , and
, and
Explicit variance computations can also be done, which show that ![]() converges in probability to
converges in probability to ![]() , but in order to go further some tools must be introduced.
, but in order to go further some tools must be introduced.
1.4.4.4 Random walk, Fourier transform, and spectral decomposition
The Markov chain ![]() on
on ![]() (microscopic representation) can be obtained by taking a sequence
(microscopic representation) can be obtained by taking a sequence ![]() of i.i.d. r.v. which are uniform on the vectors of the canonical basis, independent of
of i.i.d. r.v. which are uniform on the vectors of the canonical basis, independent of ![]() , and setting
, and setting
This is a symmetric nearest-neighbor random walk on the additive group ![]() , and we are going to exploit this structure, according to a technique adaptable to other random walks on groups.
, and we are going to exploit this structure, according to a technique adaptable to other random walks on groups.
For ![]() and
and ![]() in
in ![]() and for vectors
and for vectors ![]() and
and ![]() , the canonical scalar products will be respectively denoted by
, the canonical scalar products will be respectively denoted by
Let us associate to each r.v. ![]() on
on ![]() its characteristic function, which is the (discrete) Fourier transform of its law
its characteristic function, which is the (discrete) Fourier transform of its law ![]() given by, with the notation
given by, with the notation ![]() ,
,
For ![]() in
in ![]() and any
and any ![]() such that
such that ![]() ,
,
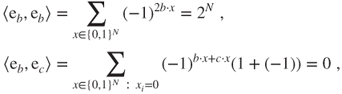
hence ![]() is an orthogonal basis of vectors, each with square product
is an orthogonal basis of vectors, each with square product ![]() . This basis could easily be transformed into an orthonormal basis.
. This basis could easily be transformed into an orthonormal basis.
Fourier inversion formula
From this follows the inversion formula
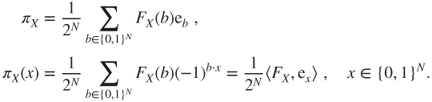
Fourier transform and eigenvalues
For ![]() , setting
, setting

it holds that
and thus ![]() is an eigenvector for the eigenvalue
is an eigenvector for the eigenvalue ![]() for the transition matrix. There are
for the transition matrix. There are ![]() distinct eigenvalues
distinct eigenvalues
of which the eigenspace of dimension ![]() is generated by the
is generated by the ![]() such that
such that ![]() has exactly
has exactly ![]() terms taking the value
terms taking the value ![]() .
.
Spectral decomposition of the transition matrix
This yields the spectral decomposition of ![]() in an orthogonal basis and
in an orthogonal basis and
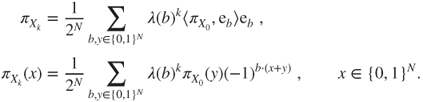
Long-time behavior
This yields that ![]() is
is ![]() for
for ![]() (constant vectors) and that
(constant vectors) and that
For ![]() , let
, let ![]() be such that
be such that ![]() ,
, ![]() and
and ![]() for
for ![]() , and
, and ![]() be the corresponding laws. Then,
be the corresponding laws. Then, ![]() and thus
and thus ![]() and
and
that is, ![]() and
and ![]() are the uniform laws respectively on
are the uniform laws respectively on
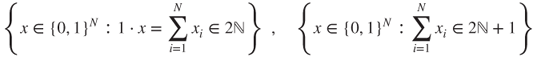
Let
The law ![]() is the mixture of
is the mixture of ![]() and
and![]() , which respects the probability that
, which respects the probability that ![]() be in
be in ![]() and in
and in ![]() , and
, and ![]() the mixture that interchanges these. If
the mixture that interchanges these. If ![]() is of law
is of law ![]() , then
, then ![]() is of law
is of law ![]() and thus
and thus
and, as ![]() and
and ![]() , for the Hilbert norm associated with
, for the Hilbert norm associated with ![]() it holds that
it holds that
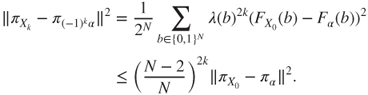
In particular, the law of ![]() converges exponentially fast to
converges exponentially fast to ![]() and the law of
and the law of ![]() to
to ![]() .
.
Periodic behavior
The behavior we have witnessed is related to the notion of periodicity: ![]() is even or odd the same as
is even or odd the same as ![]() , and
, and ![]() has opposite parity than
has opposite parity than ![]() . This is obviously related to the fact that
. This is obviously related to the fact that ![]() is an eigenvalue.
is an eigenvalue.
1.4.5 Renewal process
A component of a system (electronic component, machine, etc.) lasts a random life span before failure. It is visited at regular intervals (at times ![]() in
in ![]() ) and replaced appropriately. The components that are used for this purpose behave in i.i.d. manner.
) and replaced appropriately. The components that are used for this purpose behave in i.i.d. manner.
1.4.5.1 Modeling
At time ![]() , a first component is installed, and the
, a first component is installed, and the ![]() th component is assumed to have a random life span before replacement given by
th component is assumed to have a random life span before replacement given by ![]() , where the
, where the ![]() are i.i.d. on
are i.i.d. on ![]() . Let
. Let ![]() denote an r.v. with same law as
denote an r.v. with same law as ![]() , representing a generic life span. It is often assumed that
, representing a generic life span. It is often assumed that ![]() .
.
Let ![]() denote the age of the component in function at time
denote the age of the component in function at time ![]() , with
, with ![]() if it is replaced at that time. Setting
if it is replaced at that time. Setting
it holds that ![]() sur
sur ![]() (Figure 1.5).
(Figure 1.5).
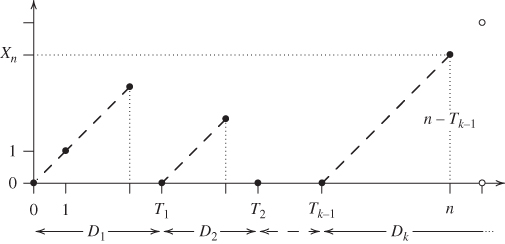
Figure 1.5 Renewal process. The • represent the ages at the discrete instants on the horizontal axis and are linearly interpolated by dashes in their increasing phases. Then, 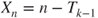 if
if 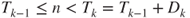 . The
. The  represent the two possible ages at time
represent the two possible ages at time  , which are
, which are  if
if 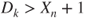 and
and 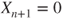 if
if  .
.
The ![]() are defined for all
are defined for all ![]() as
as ![]() . If
. If ![]() , then all
, then all ![]() are finite, a.s., else if
are finite, a.s., else if ![]() , then there exists an a.s. finite r.v.
, then there exists an a.s. finite r.v. ![]() such that
such that ![]() and
and ![]() .
.
This natural representation in terms of the life spans is not a random recursion of the kind discussed in Theorem 1.2.3. We will give a direct proof that ![]() is a Markov chain and give its transition matrix.
is a Markov chain and give its transition matrix.
Note that ![]() except if
except if ![]() and
and ![]() is in
is in ![]() for
for ![]() . These are the only cases to be considered and then
. These are the only cases to be considered and then
where ![]() is the number of
is the number of ![]() in
in ![]() and
and ![]() ,
, ![]() ,
, ![]() , … ,
, … , ![]() are their ranks (Figure 1.5). This can be written as
are their ranks (Figure 1.5). This can be written as
The independence of ![]() and
and ![]() yields that
yields that
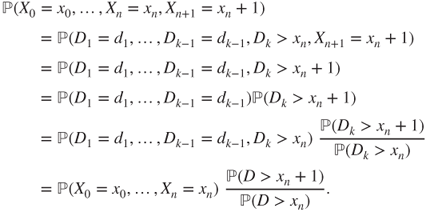
Moreover,

is obtained similarly, or by complement to ![]() .
.
Hence, the only thing that matters is the age of the component in function, and ![]() is a Markov chain on
is a Markov chain on ![]() with matrix
with matrix ![]() and graph given by
and graph given by
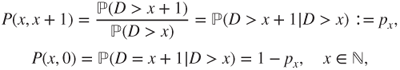

This Markov chain is irreducible if and only if ![]() for every
for every ![]() and
and ![]() .
.
A mathematically equivalent description
Thus, from a mathematical perspective, we can start with a sequence ![]() with values in
with values in ![]() and assume that a component with age
and assume that a component with age ![]() at an arbitrary time
at an arbitrary time ![]() has probability
has probability ![]() to pass the inspection at time
to pass the inspection at time ![]() , and else a probability
, and else a probability ![]() to be replaced then. In this setup, the law of
to be replaced then. In this setup, the law of ![]() is determined by
is determined by
This formulation is not as natural as the preceding one. It corresponds to a random recursion given by a sequence ![]() of i.i.d. uniform r.v. on
of i.i.d. uniform r.v. on ![]() , independent of
, independent of ![]() , and
, and
The renewal process is often introduced in this manner, in order to avoid the previous computations. It is an interesting example, as we will discuss later.
Invariant measures and laws
An invariant measure ![]() satisfies
satisfies
thus ![]() that yields uniqueness, and existence holds if and only if
that yields uniqueness, and existence holds if and only if
This unique invariant measure can be normalized, in order to yield an invariant law, if and only if it is finite, that is, if
and then
Renewal process and Doeblin condition
A class of renewal processes is one of the rare natural examples of infinite state space Markov chains satisfying the Doeblin condition.
1.4.6 Word search in a character chain
A source emits an infinite i.i.d. sequence of “characters” of some “alphabet.” We are interested in the successive appearances of a certain “word” in the sequence.
For instance, the characters could be ![]() and
and ![]() in a computer system, “red” or “black” in a roulette game, A, C, G, T in a DNA strand, or ASCII characters for a typewriting monkey. Corresponding words could be
in a computer system, “red” or “black” in a roulette game, A, C, G, T in a DNA strand, or ASCII characters for a typewriting monkey. Corresponding words could be ![]() , red-red-red-black, GAG, and Abracadabra.
, red-red-red-black, GAG, and Abracadabra.
Some natural questions are the following:
- Is any word going to appear in the sequence?
- Is it going to appear infinitely often, and with what frequency?
- What is the law and expectation of the first appearance time?
1.4.6.1 Counting automaton
A general method will be described on a particular instance, the search for the occurrences of the word GAG.
Two different kinds of occurrences can be considered, without or with overlaps; for instance, GAGAG contains one single occurrence of GAG without overlaps but two with. The case without overlaps is more difficult, and more useful in applications;it will be considered here, but the method can be readily adapted to the other case.
We start by defining a counting automaton with four states ![]() , G, GA, and GAG, which will be able to count the occurrences of GAG in any arbitrary finite character chain. The automaton starts in state
, G, GA, and GAG, which will be able to count the occurrences of GAG in any arbitrary finite character chain. The automaton starts in state ![]() and then examines the chain sequentially term by term, and:
and then examines the chain sequentially term by term, and:
- In state
 : if the next state is G, then it takes state G, else it stays in state
: if the next state is G, then it takes state G, else it stays in state  ,
, - In state G: if the next state is A, then it takes state GA, if the next state is G, then it stays in state G, else it takes state
 ,
, - In state GA: if the next state is G, then it takes state GAG, else it takes state
 ,
, - In state GAG: if the next state is G, then it takes state G, else it takes state
 .
.
Such an automaton can be represented by a graph that is similar to a Markov chain graph, with nodes given by its possible states and oriented edges between nodes marked by the logical condition for this transition (Figure 1.6).

Figure 1.6 Search for the word GAG: Markov chain graph. The graph for the automaton is obtained by replacing 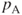 by “if the next term is
by “if the next term is 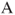 ,”
,” 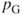 by “if the next term is
by “if the next term is  ,”
,” 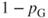 by “if the next term is not
by “if the next term is not 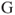 ,” and
,” and 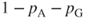 by “if the next term is neither
by “if the next term is neither 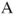 nor
nor 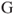 .”
.”
This automation is now used on a sequence of characters given by an i.i.d. sequence ![]() such that
such that
satisfying ![]() ,
, ![]() , and
, and ![]() .
.
Let ![]() , and
, and ![]() be the state of the automaton after having examined the
be the state of the automaton after having examined the ![]() th character. Theorem 1.2.3 yields that
th character. Theorem 1.2.3 yields that ![]() is a Markov chain with graph, given in Figure 1.6, obtained from the automaton graph by replacing the logical conditions by their probabilities of being satisfied.
is a Markov chain with graph, given in Figure 1.6, obtained from the automaton graph by replacing the logical conditions by their probabilities of being satisfied.
Markovian description
All relevant information can be written in terms of ![]() . For instance, if
. For instance, if ![]() and
and ![]() denotes the time of the
denotes the time of the ![]() th occurrence (complete, without overlaps) of the word for
th occurrence (complete, without overlaps) of the word for ![]() , and
, and ![]() the number of such occurrences taking place before
the number of such occurrences taking place before ![]() , then
, then
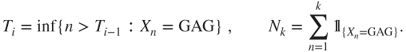
The transition matrix ![]() is irreducible and has for unique invariant law
is irreducible and has for unique invariant law

Occurrences with overlaps
In order to search for the occurrences with overlaps, it would suffice to modify the automaton by considering the overlaps inside the word. For the word GAG, we need only modify the transitions from state GAG: if the next term is G, then the automaton should take state G, and if the next term is A, then it should take state GA, else it should take state ![]() . For more general overlaps, this can become very involved.
. For more general overlaps, this can become very involved.
1.4.6.2 Snake chain
We describe another method for the search for the occurrences with overlaps of a word ![]() of length
of length ![]() in an i.i.d. sequence
in an i.i.d. sequence ![]() of characters from some alphabet
of characters from some alphabet ![]() .
.
Setting ![]() , then
, then
is the time of the ![]() th occurrence of the word,
th occurrence of the word, ![]() (with
(with ![]() ), and
), and
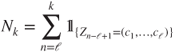
is the number of such occurrences before time ![]() . In general,
. In general, ![]() is not i.i.d., but it will be seen to be a Markov chain.
is not i.i.d., but it will be seen to be a Markov chain.
More generally, let ![]() be a Markov chain on
be a Markov chain on ![]() of arbitrary matrix
of arbitrary matrix ![]() and
and ![]() for
for ![]() . Then,
. Then, ![]() is a Markov chain on
is a Markov chain on ![]() with matrix
with matrix ![]() with only nonzero terms given by
with only nonzero terms given by
called the snake chain of length ![]() for
for ![]() . The proof is straightforward if the conditional formulation is avoided.
. The proof is straightforward if the conditional formulation is avoided.
Irreducibility
If ![]() is irreducible, then
is irreducible, then ![]() is irreducible on its natural state space
is irreducible on its natural state space
Invariant Measures and Laws
If ![]() is an invariant measure for
is an invariant measure for ![]() , then
, then ![]() given by
given by
is immediately seen to be an invariant measure for ![]() . If further
. If further ![]() is a law, then
is a law, then ![]() is also a law.
is also a law.
In the i.i.d. case where ![]() , the only invariant law for
, the only invariant law for ![]() is given by
is given by ![]() , and the only invariant law for
, and the only invariant law for ![]() by the product law
by the product law ![]() .
.
1.4.7 Product chain
Let ![]() and
and ![]() be two transition matrices on
be two transition matrices on ![]() and
and ![]() , and the matrices
, and the matrices ![]() on
on ![]() have generic term
have generic term
Then, ![]() is a transition matrix on
is a transition matrix on ![]() , as in the sense of product laws,
, as in the sense of product laws,
see below for more details. See Figure 1.7.

Figure 1.7 Product chain. The first and second coordinates are drawn independently according to  and
and  .
.
The Markov chain ![]() with matrix
with matrix ![]() is called the product chain. Its transitions are obtained by independent transitions of each coordinate according, respectively, to
is called the product chain. Its transitions are obtained by independent transitions of each coordinate according, respectively, to ![]() and
and ![]() . In particular,
. In particular, ![]() and
and ![]() are two Markov chains of matrices
are two Markov chains of matrices ![]() and
and ![]() , which conditional on
, which conditional on ![]() are independent, and
are independent, and
1.4.7.1 Invariant measures and laws
Immediate computations yield that if ![]() is an invariant measure for
is an invariant measure for ![]() and
and ![]() for
for ![]() , then the product measure
, then the product measure ![]() given by
given by
is invariant for ![]() . Moreover,
. Moreover,
and thus if ![]() and
and ![]() are laws then
are laws then ![]() is a law.
is a law.
1.4.7.2 Irreducibility problem
The matrix ![]() on
on ![]() is irreducible and has unique invariant law the uniform law, whereas a Markov chain with matrix
is irreducible and has unique invariant law the uniform law, whereas a Markov chain with matrix ![]() alternates either between
alternates either between ![]() and
and ![]() or between
or between ![]() and
and ![]() , depending on the initial state and is not irreducible on
, depending on the initial state and is not irreducible on ![]() . The laws
. The laws
are invariant for ![]() and generate the space of invariant measures.
and generate the space of invariant measures.
All this can be readily generalized to an arbitrary number of transition matrices.
Exercises
1.1 The space station, 1 An aimless astronaut wanders within a space station, schematically represented as follows:
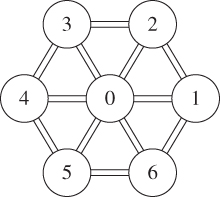
The space station spins around its center in order to create artificial gravity in its periphery. When the astronaut is in one of the peripheral modules, the probability for him to go next in each of the two adjacent peripheral modules is twice the probability for him to go to the central module. When the astronaut is in the central module, the probability for him to go next in each of the six peripheral modules is the same.
Represent this evolution by a Markov chain and give its matrix and graph. Prove that this Markov chain is irreducible and give its invariant law.
1.2 The mouse, 1 A mouse evolves in an apartment, schematically represented as follows:
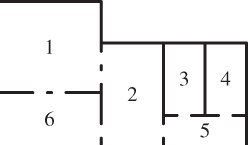
The mouse chooses uniformly an opening of the room where it is to go into a new room. It has a short memory and forgets immediately where it has come from.
Represent this evolution by a Markov chain and give its matrix and graph. Prove that this Markov chain is irreducible and give its invariant law.
1.3 Doubly stochastic matrices Let ![]() be a doubly stochastic matrix on a state space
be a doubly stochastic matrix on a state space ![]() : by definition,
: by definition,
- (a) Find a simple invariant measure for
 .
. - (b) Prove that
 is doubly stochastic for all
is doubly stochastic for all  .
. - (c) Prove that the transition matrix for a random walk on a network is doubly stochastic.
1.4 The Labouchère system, 1 In a game where the possible gain is equal to the wager, the probability of gain ![]() of the player at each draw typically satisfies
of the player at each draw typically satisfies ![]() and even
and even ![]() , but is usually close to
, but is usually close to ![]() , as when betting on red or black at roulette. In this framework, the Labouchère system is a strategy meant to provide a means for earning in a secure way a sum
, as when betting on red or black at roulette. In this framework, the Labouchère system is a strategy meant to provide a means for earning in a secure way a sum ![]() determined in advance.
determined in advance.
The sum ![]() is decomposed arbitrarily as a sum of
is decomposed arbitrarily as a sum of ![]() positive terms, which are put in a list. The strategy then transforms recursively this list, until it is empty.
positive terms, which are put in a list. The strategy then transforms recursively this list, until it is empty.
At each draw, if ![]() then the sum of the first and last terms of the list are wagered, and if
then the sum of the first and last terms of the list are wagered, and if ![]() then the single term is wagered. If the gambler wins, he or she removes from the list the terms concerned by the wager. If the gambler loses, he or she retains these terms and adds at the end of the list a term worth the sum just wagered. The game stops when
then the single term is wagered. If the gambler wins, he or she removes from the list the terms concerned by the wager. If the gambler loses, he or she retains these terms and adds at the end of the list a term worth the sum just wagered. The game stops when ![]() , and hence, the sum
, and hence, the sum ![]() has been won.
has been won.
(Martingale theory proves that in realistic situations, for instance, if wagers are bounded or credit is limited, then with a probability close to ![]() the sum
the sum ![]() is indeed won, but with a small probability a huge loss occurs, large enough to prevent the gambler to continue the game and often to ever gamble in the future.)
is indeed won, but with a small probability a huge loss occurs, large enough to prevent the gambler to continue the game and often to ever gamble in the future.)
- (a) Represent the list evolution by a Markov chain
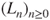 on the set
on the set
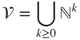
of words of the form
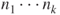 . Describe its transition matrix
. Describe its transition matrix 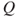 and its graph. Prove that if
and its graph. Prove that if 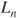 reaches
reaches  (the empty word), then the gambler wins the sum
(the empty word), then the gambler wins the sum 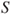 .
. - (b) Let
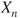 be the length of the list (or word)
be the length of the list (or word) 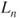 for
for 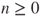 . Prove that
. Prove that  is a Markov chain on
is a Markov chain on 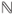 and give its matrix
and give its matrix 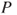 and its graph.
and its graph.
1.5 Three-card Monte Three playing cards are lined face down on a cardboard box at time ![]() . At times
. At times ![]() , the middle card is exchanged with probability
, the middle card is exchanged with probability ![]() with the card on the right and with probability
with the card on the right and with probability ![]() with the one on the left.
with the one on the left.
- (a) Represent the evolution of the three cards by a Markov chain
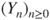 . Give its transition matrix
. Give its transition matrix 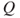 and its graph. Prove that
and its graph. Prove that 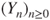 is irreducible. Find its invariant law
is irreducible. Find its invariant law 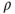 .
. - (b) The cards are the ace of spades and two reds. Represent the evolution of the ace of spades by a Markov chain
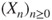 . Give its transition matrix
. Give its transition matrix 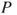 and its graph. Prove that it is irreducible. Find its invariant law
and its graph. Prove that it is irreducible. Find its invariant law 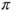 .
. - (c) Compute
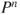 in terms of the initial law
in terms of the initial law  and
and 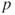 and
and 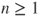 . Prove that the law
. Prove that the law 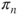 of
of  converges to
converges to 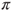 as
as 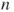 goes to infinity, give an exponential convergence rate for this convergence, and find for which value of
goes to infinity, give an exponential convergence rate for this convergence, and find for which value of 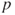 the convergence is fastest.
the convergence is fastest.
1.6 Andy, 1 If Andy is drunk one evening, then he has one odd in ten to end up in jail, in which case will remain sober the following evening. If Andy is drunk one evening and does not end up in jail, then he has one odd in two to be drunk the following evening. If Andy stays sober one evening, then he has three odds out of four to remain sober the following evening.
It is assumed that ![]() constitutes a Markov chain, where
constitutes a Markov chain, where ![]() if Andy on the
if Andy on the ![]() -th evening is drunk and ends up in jail,
-th evening is drunk and ends up in jail, ![]() if Andy then is drunk and does not end up in jail, and
if Andy then is drunk and does not end up in jail, and ![]() if then he remains sober.
if then he remains sober.
Give the transition matrix ![]() and the graph for
and the graph for ![]() . Prove that
. Prove that ![]() is irreducible and compute its invariant law. Compute
is irreducible and compute its invariant law. Compute ![]() in terms of
in terms of ![]() . What is the behavior of
. What is the behavior of ![]() when
when ![]() goes to infinity?
goes to infinity?
1.7 Squash Let us recall the original scoring system for squash, known as English scoring. If the server wins a rally, then he or she scores a point and retains service. If the returner wins a rally, then he or she becomes the next server but no point is scored. In a game, the first player to score ![]() points wins, except if the score reaches
points wins, except if the score reaches ![]() -
-![]() , in which case the returner must choose to continue in either
, in which case the returner must choose to continue in either ![]() or
or ![]() points, and the first player to reach that total wins.
points, and the first player to reach that total wins.
A statistical study of the games between two players indicates that the rallies are won by Player A at service with probability ![]() and by Player B at service with probability
and by Player B at service with probability ![]() , each in i.i.d. manner.
, each in i.i.d. manner.
The situation in which Player A has ![]() points, Player B has
points, Player B has ![]() points, and Player L is at service is denoted by
points, and Player L is at service is denoted by ![]() in
in ![]() .
.
- (a) Describe the game by a Markov chain on
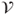 , assuming that if the score reaches
, assuming that if the score reaches 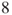 -
-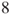 then they play on to
then they play on to  points (the play up to
points (the play up to  can easily be deduced from this), in the two following cases: (i) all rallies are considered and (ii) only point scoring is considered.
can easily be deduced from this), in the two following cases: (i) all rallies are considered and (ii) only point scoring is considered. - (b) Trace the graphs from arriving at
 -
- on the service of Player A to end of game.
on the service of Player A to end of game. - (c) A game gets to
 -
-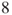 on the service of Player A. Compute in terms of
on the service of Player A. Compute in terms of  and
and 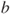 the probability that Player B wins according to whether he or she elects to go to
the probability that Player B wins according to whether he or she elects to go to  or
or 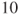 points. Counsel Player B on this difficult choice.
points. Counsel Player B on this difficult choice.
1.8 Genetic models, 1 Among the individuals of a species, a certain gene can appear under ![]() different forms called alleles.
different forms called alleles.
In a microscopic (individual centered) model for a population of ![]() individuals, these are arbitrarily numbered, and the fact that individual
individuals, these are arbitrarily numbered, and the fact that individual ![]() carries allele
carries allele ![]() is coded by the state
is coded by the state
A macroscopic representation only retains the numbers of individuals carrying each allele, and the state space is
We study two simplified models for the reproduction of the species, in which the population size is fixed, and where the selective advantage of every allele ![]() w.r.t. the others is quantified by a real number
w.r.t. the others is quantified by a real number ![]() .
.
- Synchronous: Fisher–Wright model: at each step, the whole population is replaced by its descendants, and in i.i.d. manner, each new individual carries allele
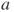 with a probability proportional both to
with a probability proportional both to 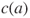 and to the number of old individuals carrying allele
and to the number of old individuals carrying allele 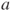 .
. - Asynchronous: Moran model: at each step, an uniformly chosen individual is replaced by a new individual, which carries allele
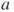 with a probability proportional both to
with a probability proportional both to 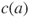 and to the number of old individuals carrying allele
and to the number of old individuals carrying allele  .
.
- Explain how to obtain the macroscopic representation from the microscopic representation
- Prove that each pair representation-model corresponds to a Markov chain. Give the transition matrices and the absorbing states.
1.9 Records Let ![]() be i.i.d. r.v. such that
be i.i.d. r.v. such that ![]() and
and ![]() , and
, and ![]() be the greatest number of consecutive
be the greatest number of consecutive ![]() observed in
observed in ![]() .
.
- (a) Show that
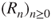 is not a Markov chain.
is not a Markov chain. - (b) Let
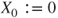 , and
, and
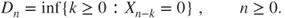
Prove that
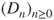 is a Markov chain and give its transition matrix
is a Markov chain and give its transition matrix 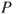 . Prove that there exists a unique invariant law
. Prove that there exists a unique invariant law 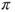 and compute it.
and compute it. - (c) Let
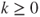 ,
,
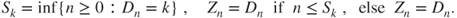
Prove that
 is a Markov chain on
is a Markov chain on 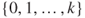 and give its transition matrix
and give its transition matrix 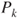 .
. - (d) Express
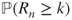 in terms of
in terms of 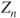 , then of
, then of  . Deduce from this the law of
. Deduce from this the law of 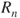 .
. - (e) What is the probability of having at least
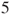 consecutive heads among
consecutive heads among 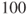 fair tosses of head-or-tails? One can use the fact that for
fair tosses of head-or-tails? One can use the fact that for 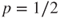 ,
,

1.10 Incompressible mixture, 1 There are two urns, ![]() white balls, and
white balls, and ![]() black balls. Initially
black balls. Initially ![]() balls are set in each urn. In i.i.d. manner, a ball is chosen uniformly in each urn and the two are interchanged. The white balls are numbered from
balls are set in each urn. In i.i.d. manner, a ball is chosen uniformly in each urn and the two are interchanged. The white balls are numbered from ![]() to
to ![]() and the black balls from
and the black balls from ![]() to
to ![]() . We denote by
. We denote by ![]() the r.v. with values in
the r.v. with values in
given by the set of the numbers in the first urn just after time ![]() and by
and by
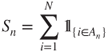
the corresponding number of white balls.
- (a) Prove that
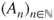 is an irreducible Markov chain on
is an irreducible Markov chain on 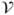 and give its matrix
and give its matrix 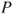 . Prove that the invariant law
. Prove that the invariant law  is unique and compute it.
is unique and compute it. - (b) Do the same for
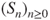 on
on 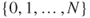 , with matrix
, with matrix 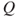 and invariant law
and invariant law 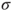 .
. - (c) For
 find a recursion for
find a recursion for 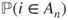 , and solve it in terms of
, and solve it in terms of 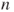 and
and 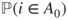 . Do likewise for
. Do likewise for  . What happens for large
. What happens for large 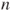 ?
?
1.11 Branching with immigration The individuals of a generation disappear at the following, leaving there ![]() descendants each with probability
descendants each with probability ![]() , and in addition,
, and in addition, ![]() immigrants appear with probability
immigrants appear with probability ![]() , where
, where ![]() . Let
. Let
be the generating functions for the reproduction and the immigration laws.
Similarly to Section 1.4.3, using ![]() with values in
with values in ![]() and
and ![]() and
and ![]() for
for ![]() and
and ![]() such that
such that ![]() and
and ![]() for
for ![]() in
in ![]() , all these r.v. being independent, let us represent the number of individuals in generation
, all these r.v. being independent, let us represent the number of individuals in generation ![]() by
by
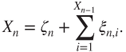
Let ![]() be the generating function of
be the generating function of ![]() .
.
- (a) Prove that
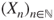 is a Markov chain, without giving its transition matrix.
is a Markov chain, without giving its transition matrix. - (b) Compute
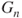 in terms of
in terms of 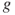 ,
, 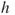 , and
, and 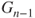 , then of
, then of 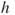 ,
,  ,
, 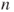 , and
, and 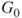 .
. - (c) If
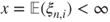 and
and 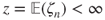 , compute
, compute 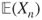 in terms of
in terms of 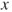 ,
, 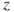 ,
, 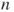 , and
, and 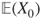 .
.
1.12 Single Server Queue Let ![]() be i.i.d. r.v. with values in
be i.i.d. r.v. with values in ![]() , with generating function
, with generating function ![]() and expectation
and expectation ![]() , and let
, and let ![]() be an independent r.v. with values in
be an independent r.v. with values in ![]() . Let
. Let
- (a) Prove that
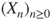 is a Markov chain with values in
is a Markov chain with values in 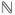 , which is irreducible if and only if
, which is irreducible if and only if 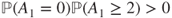 .
. - (b) Compute
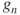 in terms of
in terms of 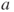 and
and 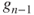 .
. - (c) It is now assumed that there exists an invariant law
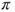 for
for  , with generating function denoted by
, with generating function denoted by 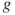 . Prove that
. Prove that
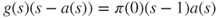
and that
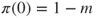 .
. - (d) Prove that necessarily
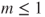 and that
and that 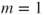 only in the trivial case where
only in the trivial case where 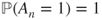 .
. - (e) Let
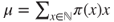 . Prove that
. Prove that  if and only if
if and only if 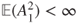 , and then that for
, and then that for 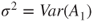 , it holds that
, it holds that  .
.
1.13 Dobrushin mixing coefficient Let ![]() be a transition matrix on
be a transition matrix on ![]() , and
, and
- (a) Prove that
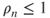 and that, for all laws
and that, for all laws 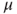 and
and 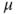 ,
,
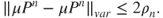
- (b) Prove that
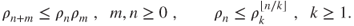
One may use that
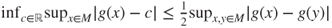 .
. - (c) Prove that if
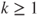 is such that
is such that 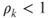 , then
, then  is a Cauchy sequence, its limit is an invariant law
is a Cauchy sequence, its limit is an invariant law 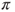 , and
, and
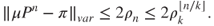
- (d) Assume that
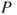 satisfies the Doeblin condition: there exists
satisfies the Doeblin condition: there exists 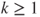 and
and 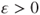 and a law
and a law 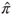 such that
such that 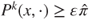 . Prove that
. Prove that  . Compare with the result in Theorem 1.3.4.
. Compare with the result in Theorem 1.3.4. - (e) Let
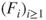 be a sequence of i.i.d. random functions from
be a sequence of i.i.d. random functions from 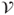 to
to 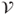 , and
, and 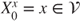 and
and 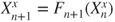 for
for  , so that
, so that  is the transition matrix of the Markov chain induced by this random recursion, see Theorem 1.2.3 and what follows. Let
is the transition matrix of the Markov chain induced by this random recursion, see Theorem 1.2.3 and what follows. Let
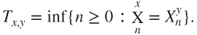
Prove that