4.3 Elements on the rate of convergence for laws
A modern field of study investigates the rates of convergence for the Kolmogorov ergodic theorem. The scope is to help develop and validate Monte Carlo methods for the approximate simulation from laws, which will be described in Section 5.2. One of the objectives of this section is to facilitate the reading of advanced books on the subject, such as Duflo, M. (1996) and Saloff-Coste, L. (1997). The latter book provides many examples of explicit refined bounds of convergence in law.
We are going to describe the functional analysis framework which is at the basis of the simplest aspects of these studies, which is an extension of the concepts in Section 1.3. If ![]() is finite, then powerful results can be obtained by classic tools of finite dimensional linear algebra, which they thus illustrate. If
is finite, then powerful results can be obtained by classic tools of finite dimensional linear algebra, which they thus illustrate. If ![]() is infinite, extensions of these tools will be introduced, such as those described in the book of Rudin, W. (1991).
is infinite, extensions of these tools will be introduced, such as those described in the book of Rudin, W. (1991).
4.3.1 The Hilbert space framework
4.3.1.1 Fundamental Hilbert space, adjoints, and time reversal
Let ![]() be an irreducible positive recurrent Markov chain on
be an irreducible positive recurrent Markov chain on ![]() with matrix
with matrix ![]() , and
, and ![]() be its invariant law. Consider the functional Hilbert space
be its invariant law. Consider the functional Hilbert space ![]() , in which the scalar product of
, in which the scalar product of ![]() and
and ![]() is given by
is given by
A fundamental probabilistic interpretation is that
The matrix ![]() of the time reversal in equilibrium of
of the time reversal in equilibrium of ![]() satisfies
satisfies
Hence, ![]() is the adjoint of
is the adjoint of ![]() in
in ![]() , and
, and ![]() is reversible for
is reversible for ![]() if and only if
if and only if ![]() is self-adjoint in
is self-adjoint in ![]() . The link between adjoints and time reversal can be seen in
. The link between adjoints and time reversal can be seen in
4.3.1.2 Duality between measures and functions, identification of measures and their densities
The natural duality bracket between measures and functions
allows to identify the dual space ![]() with a subspace of
with a subspace of ![]() . The Cauchy–Schwarz inequality yields that
. The Cauchy–Schwarz inequality yields that

with equality if ![]() is equal to the density
is equal to the density ![]() of
of ![]() w.r.t.
w.r.t. ![]() . Thus,
. Thus, ![]() is a Hilbert space included in
is a Hilbert space included in ![]() , with scalar product given, for
, with scalar product given, for ![]() and
and ![]() , by
, by
which is the scalar product in ![]() of their densities w.r.t.
of their densities w.r.t. ![]() . The adjoint of
. The adjoint of ![]() on
on ![]() is the operator
is the operator ![]() on
on ![]() , which has norm
, which has norm ![]() , and
, and

Duality formulae
The following duality formulae should be kept in mind:
Choice of identifications and duality
These computations become clearer if we use as a reference duality bracket the scalar product of ![]() itself, which identifies it with its own dual
itself, which identifies it with its own dual ![]() . For
. For ![]() and
and ![]() ,
,
which identifies ![]() to its density
to its density ![]() and
and ![]() to
to ![]() . Note that the total variation norm can be expressed as the
. Note that the total variation norm can be expressed as the ![]() norm of the densities.
norm of the densities.
We elect to use the natural duality already used in Section 1.3 and use the duality formulae (3.8), even though the notations ![]() and
and ![]() are compatible with both duality frameworks.
are compatible with both duality frameworks.
This duality could be identified with the natural duality between the sequence spaces ![]() and
and ![]() , in which case
, in which case ![]() and
and ![]() are identified with the spaces
are identified with the spaces ![]() and
and ![]() of square-summable sequences with the corresponding weights, and the space
of square-summable sequences with the corresponding weights, and the space ![]() is the pivot space in the Gelfand triple
is the pivot space in the Gelfand triple
All this makes for a better understanding of Section 3.3.3.
4.3.1.3 Simple bounds and orthogonal projections
4.3.2 Dirichlet form, spectral gap, and exponential bounds
4.3.2.1 Dirichlet form, spectral gap, and Poincaré inequality
The notations ![]() and
and ![]() can be used if the context is clear. If
can be used if the context is clear. If ![]() , then often it is said that “there is a spectral gap.”
, then often it is said that “there is a spectral gap.”
4.3.2.2 Exponential bounds for convergence in law
Exponential convergence
This almost tautological result justifies the notions that have been introduced: if ![]() , then
, then ![]() provides a geometric convergence rate for
provides a geometric convergence rate for ![]() toward
toward ![]() . If
. If ![]() is finite, it is so as soon as
is finite, it is so as soon as ![]() is irreducible, and this will be generalized to an arbitrary irreducible aperiodic matrix
is irreducible, and this will be generalized to an arbitrary irreducible aperiodic matrix ![]() in Exercise 4.10.
in Exercise 4.10.
If ![]() is not irreducible or is not aperiodic, clearly
is not irreducible or is not aperiodic, clearly ![]() and
and ![]() are not irreducible, and then
are not irreducible, and then ![]() . Exercise 4.6 will show that
. Exercise 4.6 will show that ![]() or
or ![]() may well not be irreducible, even if
may well not be irreducible, even if ![]() is irreducible aperiodic.
is irreducible aperiodic.
Spectral gap bounds
An effective method for finding explicit lower bounds for the spectral gap can be to establish Poincaré inequalities using graph techniques. This will be done in Exercises 4.11 and 4.12. This technique is developed on many examples in Duflo, M. (1996) and Saloff-Coste, L. (1997), Chapter 3.
4.3.2.3 Application to the chain with two states
The Markov chain on ![]() with matrix
with matrix ![]() for
for ![]() is irreducible if and only if
is irreducible if and only if ![]() and aperiodic if and only if
and aperiodic if and only if ![]() .
.
If ![]() , then
, then ![]() , any law is invariant, and
, any law is invariant, and ![]() . Else, the only invariant law is
. Else, the only invariant law is ![]() and
and ![]() is reversible for
is reversible for ![]() , and
, and ![]() if and only if
if and only if ![]() . Moreover,
. Moreover,
and ![]() and
and ![]() imply that, up to sign for
imply that, up to sign for ![]() ,
,
Thus, ![]() varies continuously, between
varies continuously, between ![]() when
when ![]() and the chain is not irreducible and
and the chain is not irreducible and ![]() when
when ![]() and the chain has period
and the chain has period ![]() .
.
As ![]() and hence
and hence ![]() and
and
and the explicit form for ![]() given in Section 1.3.3 shows that the exponential bounds in Theorem 4.3.5 cannot be improved.
given in Section 1.3.3 shows that the exponential bounds in Theorem 4.3.5 cannot be improved.
4.3.3 Spectral theory for reversible matrices
4.3.3.1 General principles
The spectrum ![]() of a bounded operator
of a bounded operator ![]() on a Banach space is the set of all
on a Banach space is the set of all ![]() such that
such that ![]() is not invertible. The spectral radius is given by
is not invertible. The spectral radius is given by ![]() .
.
If ![]() is a transition matrix having an invariant law
is a transition matrix having an invariant law ![]() , then
, then ![]() is reversible w.r.t.
is reversible w.r.t. ![]() and
and ![]() , and
, and ![]() and
and ![]() are both reversible w.r.t.
are both reversible w.r.t. ![]() and nonnegative:
and nonnegative: ![]() and
and ![]() . In this way, we can reduce some problems to reversible matrices. These correspond to self-adjoint operators on a Hilbert space, of which the spectral theory is a powerful tool developed, for example, in Rudin, W. (1991), Chapter 12.
. In this way, we can reduce some problems to reversible matrices. These correspond to self-adjoint operators on a Hilbert space, of which the spectral theory is a powerful tool developed, for example, in Rudin, W. (1991), Chapter 12.
If ![]() is an irreducible transition matrix on a state space
is an irreducible transition matrix on a state space ![]() , which is reversible w.r.t. a probability measure
, which is reversible w.r.t. a probability measure ![]() , then
, then ![]() is self-adjoint in the Hilbert space
is self-adjoint in the Hilbert space ![]() , and hence, its spectrum
, and hence, its spectrum ![]() is real, see Rudin, W. (1991) Theorem 12.15. Theorem 4.2.15 then yields that the only elements of the spectrum of modulus
is real, see Rudin, W. (1991) Theorem 12.15. Theorem 4.2.15 then yields that the only elements of the spectrum of modulus ![]() can be
can be ![]() (always a simple eigenvalue) and
(always a simple eigenvalue) and ![]() and that
and that ![]() is in the spectrum if and only if
is in the spectrum if and only if ![]() has period
has period ![]() and then it is a simple eigenvalue.
and then it is a simple eigenvalue.
4.3.3.2 Finite state spaces
Let ![]() be an irreducible transition matrix, which is reversible w.r.t. a probability measure
be an irreducible transition matrix, which is reversible w.r.t. a probability measure ![]() , on a finite state space
, on a finite state space ![]() .
.
Classic results of linear algebra and Theorem 4.2.15 yield that the spectrum ![]() is constituted of
is constituted of ![]() (possibly repeated) real eigenvalues
(possibly repeated) real eigenvalues
and that ![]() can be diagonalized in an orthonormal basis of
can be diagonalized in an orthonormal basis of ![]() constituted of corresponding eigenvectors
constituted of corresponding eigenvectors ![]() ,
, ![]() , … ,
, … , ![]() . This yields the spectral decomposition
. This yields the spectral decomposition
in which
denotes the orthogonal projection in ![]() on the eigenspace of
on the eigenspace of ![]() . The expression in terms of these projections is unique, even though the orthonormal basis is not.
. The expression in terms of these projections is unique, even though the orthonormal basis is not.
Setting
for ![]() , it holds that
, it holds that
with equality if and only if ![]() is in the vector space generated by the eigenvalues with modulus
is in the vector space generated by the eigenvalues with modulus ![]() . If
. If ![]() has period
has period ![]() , then
, then ![]() is an eigenvalue and hence
is an eigenvalue and hence ![]() , else if
, else if ![]() is aperiodic, then
is aperiodic, then ![]() gives the geometric rate of convergence. The corresponding result for
gives the geometric rate of convergence. The corresponding result for ![]() is obtained analogously or by duality.
is obtained analogously or by duality.
Ehrenfest Urn
As an example, we refer to the macroscopic description of the Ehrenfest Urn in Section 1.4.4. Its eigenvalues are of the form
the latter as ![]() has period
has period ![]() . Moreover, the corresponding eigenvectors were computed.
. Moreover, the corresponding eigenvectors were computed.
4.3.3.3 General state spaces
When ![]() is infinite, the spectral decomposition in terms of orthogonal projections (3.9) can be generalized in integral form into a resolution of the identity, using the spectral theorem given, for example, in Rudin, W. (1991) Theorem 12.23. This yields results analogous to (3.10). We state without further explanations the following important result, which we have just proved when
is infinite, the spectral decomposition in terms of orthogonal projections (3.9) can be generalized in integral form into a resolution of the identity, using the spectral theorem given, for example, in Rudin, W. (1991) Theorem 12.23. This yields results analogous to (3.10). We state without further explanations the following important result, which we have just proved when ![]() is finite and hence,
is finite and hence, ![]() is finite dimensional, and which is still classic in infinite dimensions.
is finite dimensional, and which is still classic in infinite dimensions.
If ![]() , then
, then ![]() and
and ![]() converge to
converge to ![]() exponentially as
exponentially as ![]() goes to infinity. Moreover,
goes to infinity. Moreover, ![]() if and only if
if and only if ![]() or
or ![]() are in the closure of
are in the closure of ![]() , which can happen when
, which can happen when ![]() is infinite even when
is infinite even when ![]() is irreducible aperiodic. In this situation, a modern research topic is to establish polynomial rates of convergence bounds.
is irreducible aperiodic. In this situation, a modern research topic is to establish polynomial rates of convergence bounds.
4.3.3.4 Relation with spectral gaps and Dirichlet forms
The advantage of the Dirichlet form techniques is that they can be applied to a transition matrix ![]() which is not necessarily reversible w.r.t. its invariant law
which is not necessarily reversible w.r.t. its invariant law ![]() . Moreover, it is often difficult to estimate a spectrum, and the following result allows the estimation of
. Moreover, it is often difficult to estimate a spectrum, and the following result allows the estimation of ![]() from the spectral gap
from the spectral gap ![]() , and the latter can often be estimated using, for instance, Poincaré inequalities.
, and the latter can often be estimated using, for instance, Poincaré inequalities.
4.3.4 Continuous-time Markov chains
The theory of continuous-time Markov chains ![]() is simpler than the theory for discrete-time Markov chains for everything concerning the long-time limits of the instantaneous law and their rates of convergence, for instance in terms of Dirichlet forms, spectral gaps, and spectral theory. Notably, the notion of period disappears.
is simpler than the theory for discrete-time Markov chains for everything concerning the long-time limits of the instantaneous law and their rates of convergence, for instance in terms of Dirichlet forms, spectral gaps, and spectral theory. Notably, the notion of period disappears.
If the generator (or ![]() -matrix)
-matrix) ![]() is bounded as an operator on
is bounded as an operator on ![]() , that is, if
, that is, if
then the transition semigroup ![]() with generic term
with generic term ![]() is given by the sum of the exponential series
is given by the sum of the exponential series
which is normally convergent for the operator norm ![]() , and the Gronwall Lemma yields that it is the unique solution of the Kolmogorov equations
, and the Gronwall Lemma yields that it is the unique solution of the Kolmogorov equations
Moreover, ![]() for some transition matrix
for some transition matrix ![]() , and the evolution of a continuous-time Markov chain with bounded generator
, and the evolution of a continuous-time Markov chain with bounded generator ![]() corresponds to jumping at the instants of a Poisson process of intensity
corresponds to jumping at the instants of a Poisson process of intensity ![]() according to a discrete-time Markov chain with transition matrix
according to a discrete-time Markov chain with transition matrix ![]() .
.
Hence, Saloff-Coste, L. (1997, Sections 1.3.1 and 2.1.1) considers the continuous-time Markov chain with generator ![]() . The first inequality of the proof of Theorem 4.3.5 is replaced if
. The first inequality of the proof of Theorem 4.3.5 is replaced if ![]() by
by

obtained by the Kolmogorov equations and the differentiation of bilinear forms, yielding the inequalities
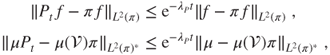
in which the spectral gap ![]() appears directly. If
appears directly. If ![]() and hence
and hence ![]() are reversible, formulae such as (3.10) become
are reversible, formulae such as (3.10) become
in which ![]() is again the spectral gap, which explains this denomination.
is again the spectral gap, which explains this denomination.
Exercises
4.1 The space station, the mouse, and three-card Monte See Exercises 1.1, 1.2, and 1.5.
- (a) What is the asymptotics for the proportion of time in which the astronaut is in the central unit? in which the mouse is in room
 ? in which the three cards are in their initial positions?
? in which the three cards are in their initial positions? - (b) Find the periods of the chains.
- (c) After a very long period of time, an asteroid hits one of the peripheral units of the space station. Estimate the probability that the astronaut happens to be in the unit when this happens.
- (d) The entrance door of the apartment is in room
 , and after a very long period of time, the tenant comes back home. Give an approximation for the probability that he does so precisely when the mouse is in room
, and after a very long period of time, the tenant comes back home. Give an approximation for the probability that he does so precisely when the mouse is in room  .
. - (e) For three-card Monte, give an approximation of the probability that after
 steps the three cards are in their initial positions. Same question after
steps the three cards are in their initial positions. Same question after 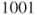 steps.
steps. - (f) For three-card Monte, an on-looker waits for a large number of card exchanges and then designates the middle card as the ace of spades. He bets
 dollars, which he will loose if he is wrong and which will be given back to him with an additional
dollars, which he will loose if he is wrong and which will be given back to him with an additional 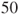 dollars if he is right. Give an approximation for the expectation of the sum he will end up with. If
dollars if he is right. Give an approximation for the expectation of the sum he will end up with. If  and this large number is
and this large number is 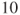 , give an order of magnitude in the error made in this approximation.
, give an order of magnitude in the error made in this approximation.
4.2 Difficult advance, see Exercise 3.9 For ![]() , give the long-time limit of the probability that the chain is in
, give the long-time limit of the probability that the chain is in ![]() . For
. For ![]() , give for
, give for ![]() the long-time limit of the ratio between the time spent in
the long-time limit of the ratio between the time spent in ![]() and the time spent in
and the time spent in ![]() .
.
4.3 Queue with ![]() servers, see Exercise 3.10 When
servers, see Exercise 3.10 When ![]() , give the long-time limit of the fraction of time that all
, give the long-time limit of the fraction of time that all ![]() servers are operating simultaneously.
servers are operating simultaneously.
4.4 Centered random walk, 1-d On ![]() , let
, let ![]() be a sequence of i.i.d. integrable r.v.,
be a sequence of i.i.d. integrable r.v., ![]() be an independent r.v., and
be an independent r.v., and ![]() be the corresponding random walk. Let
be the corresponding random walk. Let ![]() , recall that then
, recall that then ![]() is null recurrent, and let
is null recurrent, and let ![]() and
and ![]() . Let
. Let ![]() and
and ![]() for
for ![]() .
.
- (a) Prove that the Markov chain is irreducible on
 , that the uniform measure is the unique invariant measure, and that the
, that the uniform measure is the unique invariant measure, and that the 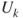 are stopping times.
are stopping times. - (b) Prove that if
 , then
, then  .
. - (c) Prove that if
 , then
, then
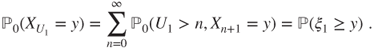
- (d) Prove that the
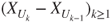 are i.i.d. and have same law as
are i.i.d. and have same law as 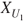 when
when  .
. - (e) Let now
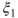 be square integrable, and
be square integrable, and 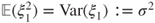 . Prove that
. Prove that 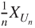 converges a.s. to
converges a.s. to 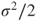 .
.
4.5 Period and adjoint Let ![]() be an irreducible transition matrix with period
be an irreducible transition matrix with period ![]() having an invariant measure
having an invariant measure ![]() , and
, and ![]() the adjoint of
the adjoint of ![]() w.r.t.
w.r.t. ![]() . Prove that
. Prove that ![]() has period
has period ![]() and describe its decomposition in aperiodic classes. Are the matrices
and describe its decomposition in aperiodic classes. Are the matrices ![]() and
and ![]() irreducible?
irreducible?
4.6 Renewal process Let ![]() , the renewal process
, the renewal process ![]() with
with ![]() and
and ![]() , and its matrix
, and its matrix ![]() .
.
- (a) Prove that
 is irreducible, aperiodic, and positive recurrent.
is irreducible, aperiodic, and positive recurrent. - (b) Give the limit for large
 of
of  .
. - (c) Give the long-time limit of the instantaneous probability that the age of the component is greater than or equal to
 . Give a bound for the distance between this limit probability and the probability at time
. Give a bound for the distance between this limit probability and the probability at time 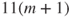 .
. - (d) Determine for
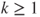 the recurrent classes of the matrices
the recurrent classes of the matrices 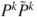 and
and 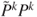 . For which
. For which  are these matrices irreducible?
are these matrices irreducible?
4.7 Distance to equilibrium Let ![]() be an irreducible Markov chain on
be an irreducible Markov chain on ![]() with matrix
with matrix ![]() having an invariant law
having an invariant law ![]() .
.
- (a) Prove that, for
 in
in  and
and  in
in 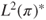 and
and  ,
,
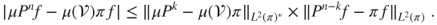
- (b) Prove that if
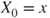 , then
, then 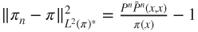 .
.
4.8 Dirichlet form Let ![]() be an irreducible transition matrix and
be an irreducible transition matrix and ![]() an invariant measure. As a generalization of the Dirichlet form, for
an invariant measure. As a generalization of the Dirichlet form, for ![]() in
in ![]() , let
, let ![]() .
.
- (a) Let
 . Prove that
. Prove that 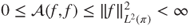 , that
, that  if and only if
if and only if  is constant, and that
is constant, and that

- (b) Prove that any nonnegative subharmonic function of
 is constant. Generalize to lower-bounded subharmonic functions.
is constant. Generalize to lower-bounded subharmonic functions. - (c) Let
 be harmonic and in
be harmonic and in 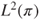 . Prove that
. Prove that 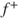 and
and  are subharmonic. Conclude that
are subharmonic. Conclude that  is constant.
is constant.
4.9 Spectral gap bounds Let ![]() be an irreducible transition matrix on
be an irreducible transition matrix on ![]() having an invariant law
having an invariant law ![]() , and
, and ![]() .
.
- (a) Prove that
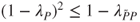 .
. - (b) Prove that if
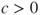 , then
, then 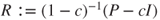 is an irreducible transition matrix, and that
is an irreducible transition matrix, and that 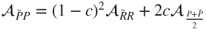 . Deduce from this that
. Deduce from this that 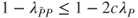 .
. - (c) Prove that if
 , then
, then 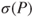 is included in the complex half-plane of nonnegative real parts.
is included in the complex half-plane of nonnegative real parts.
4.10 Exponential bounds Let ![]() be an irreducible transition matrix on
be an irreducible transition matrix on ![]() having an invariant law
having an invariant law ![]() .
.
- (a) Prove that, for
 and
and  and
and 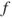 in
in 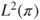 and
and 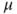 in
in  ,
,

- (b) Prove that if
 is finite and
is finite and  is aperiodic, then there exists
is aperiodic, then there exists  such that
such that 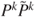 is strongly irreducible. Deduce from this some exponential convergence bounds.
is strongly irreducible. Deduce from this some exponential convergence bounds.
4.11 Poincaré inequality and graphs Let ![]() be an irreducible transition matrix on
be an irreducible transition matrix on ![]() which is reversible w.r.t. a law
which is reversible w.r.t. a law ![]() , and
, and
Choose a length function ![]() , for every
, for every ![]() a simple path
a simple path
in which ![]() are distinct elements of
are distinct elements of ![]() , and let
, and let

- (a) Prove that
 . Of which Markov chain, is this the Dirichlet form?
. Of which Markov chain, is this the Dirichlet form? - (b) Prove that, for
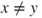 and
and  in
in 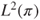 ,
,

Deduce from this that

- (c) Prove that
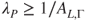 .
.
4.12 Spectral gap of the M/M/1 queue The results of Exercise 4.11 are now going to be applied to the random walk with reflection at ![]() on
on ![]() with matrix
with matrix ![]() given by
given by ![]() and
and ![]() . Let
. Let ![]() and
and ![]() for
for ![]() in
in ![]() .
.
- (a) Check that
 is irreducible, aperiodic, and reversible for
is irreducible, aperiodic, and reversible for 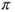 . Check that any
. Check that any 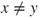 in
in 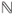 are linked by a simple path
are linked by a simple path 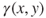 , which goes from neighbor to neighbor. Check that if the length function satisfies
, which goes from neighbor to neighbor. Check that if the length function satisfies 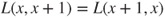 , then
, then

- (b) Prove that the choice
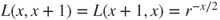 for
for 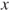 in
in 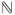 yields
yields
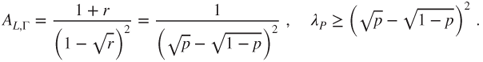
Actually, this bound is the exact value for the spectral gap, which is well known as
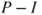 is the generator of the continuous-time Markov chain of the number of jobs in an
is the generator of the continuous-time Markov chain of the number of jobs in an 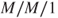 queue.
queue.
4.13 Entropy Let ![]() with
with ![]() . For laws
. For laws ![]() and
and ![]() on
on ![]() , the relative entropy of
, the relative entropy of ![]() w.r.t.
w.r.t. ![]() is defined by
is defined by
- (a) Prove that
 is strictly convex and continuous on
is strictly convex and continuous on 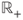 and that
and that  is strictly convex and continuous with values
is strictly convex and continuous with values  and vanishes if and only if
and vanishes if and only if 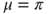 .
. - (b) Let
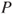 be an irreducible transition matrix on
be an irreducible transition matrix on 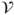 with an invariant law
with an invariant law 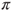 . Prove that
. Prove that  and that if there exists
and that if there exists  such that
such that  for all
for all  , then
, then  if and only if
if and only if  . The adjoint
. The adjoint 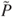 can be used for this.
can be used for this. - (c) Let
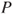 hereafter be aperiodic, and the state space
hereafter be aperiodic, and the state space 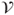 be finite. Prove that there exists
be finite. Prove that there exists  such that
such that  and that
and that  is relatively compact.
is relatively compact. - (d) Prove that the limits
 and
and 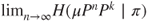 exist and are equal. For any accumulation point
exist and are equal. For any accumulation point  of
of 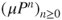 , prove that
, prove that  , and deduce from this that
, and deduce from this that  . Conclude that
. Conclude that 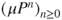 converges to
converges to  .
.

