Equipment Failure
Abstract
In previous chapters, the primary area of interest was consequence modeling at multiscale levels such as assessment of thermal hazards from fire, dispersion modeling of hazardous gases, consequence modeling of explosion, and estimation of safety parameters relevant to flammable and toxic chemicals. In safety analysis, consequence modeling is necessary but not a sufficient step. Consequence modeling addresses the question: How severe can a process safety incident be? It does not address: How often could it happen? The likelihood of a process safety event is thus very important for performing a quantitative risk assessment study of a given scenario. Some of the information that helps estimate the likelihood of an event are ignition probability (early for fire and late for explosion), weather data (wind speed, direction, temperature, etc.), and equipment failure rate. Among these, the failure of equipment such as that of a pump, a compressor, a pressure vessel, or a specific-diameter pipeline typically initiates a process safety event. In the following, various approaches applicable to estimation of equipment failure rate are explored. In addition, modeling methodologies that can help understand the underlying mechanism behind equipment failure is demonstrated.
Keywords
Bayesian; Bayesian logic; Corrosion; Crack propagation; Deformation; Equipment failure; Failure rate; LOPA; Molecular dynamics; Offshore pipeline; Quantitative risk assessment; Quantum mechanics; Risk7.1. Introduction
7.2. Failure Rates for Various Types of Equipment
7.2.1. Examining Extrapolation of Current Data Outside Their Applicable Domain of Certain Temperature and Pressure Failure Rate of Equipment
7.2.1.1. Mean time to failure
7.2.1.2. Exponential distribution
![]() (7.1)
(7.1)
![]() (7.2)
(7.2)
7.2.1.3. Gamma distribution
![]() (7.3)
(7.3)
Table 7.1
Summary of the Lifetime Distributions
| Distribution Characteristic | Exponential Distribution | Weibull Distribution | Normal Distribution | Lognormal Distribution |
| PDF, f(t) | λ exp(−λt) |
|
|
|
| CDF, F(t) | 1 − exp(−λt) |
|
|
|
| Instantaneous failure rate, h(t) | λ |
|
|
|
| MTTF |
|
|
μ |
|

 (7.4)
(7.4)
 (7.5)
(7.5)
7.2.1.4. Weibull distribution
 (7.6)
(7.6)
![]() (7.7)
(7.7)
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
7.2.1.5. Normal distribution
 (7.10)
(7.10)
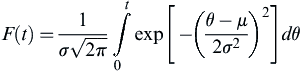 (7.11)
(7.11)
![]() (7.12)
(7.12)
7.2.1.6. Lognormal distribution
![]() (7.13)
(7.13)
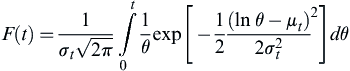 (7.14)
(7.14)
![]()
![]() (7.15)
(7.15)
7.2.1.7. Failure rates without failure
![]() (7.16)
(7.16)
![]() (7.17)
(7.17)
![]() (7.18)
(7.18)
![]() (7.19)
(7.19)
![]() (7.20)
(7.20)
![]() (7.21)
(7.21)
![]() (7.22)
(7.22)
![]() (7.23)
(7.23)
7.2.2. Bayesian Logic
7.2.2.1. Introduction to the Bayes theorem
![]() (7.24)
(7.24)
![]() (7.25)
(7.25)
7.2.2.2. An illustrative example of Bayes theorem
![]() (7.26)
(7.26)
Table 7.2
Initial Values for the Die Roll Example
| Components | Defined Probabilities | Value |
| “Reliability” | P(F) = probability of fair die | 0.5 |
| P(L) = probability of loaded die | 0.5 | |
| “Test” | P(S|F) = probability of 6 given a fair die | 0.167 |
| P(S′|F) = probability of not 6 given a fair die | 0.833 | |
| P(S|L) = probability of 6 given a loaded die | 0.9 | |
| P(S′|L) = probability of not 6 given a loaded die | 0.1 |

![]() (7.27)
(7.27)
7.2.2.3. Bayes theorem and application to equipment failure
 (7.28)
(7.28)
![]() (7.29)
(7.29)
![]() (7.30)
(7.30)
![]() (7.31)
(7.31)
![]() (7.32)
(7.32)
 (7.33)
(7.33)
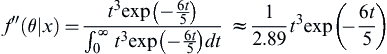 (7.34)
(7.34)
7.2.2.4. Sources of generic data
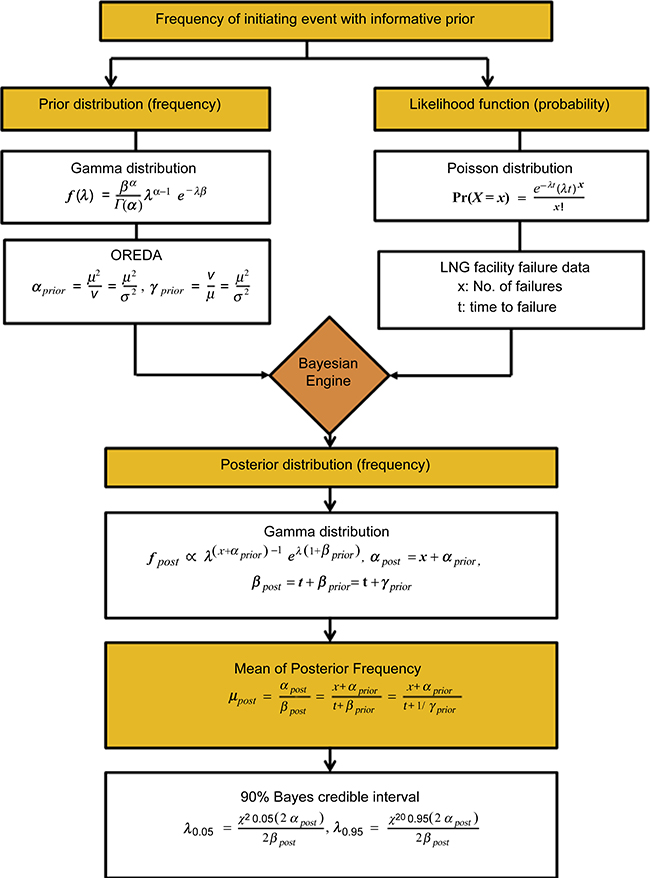
7.2.3. Risk Assessment of LNG Terminals Using the Bayesian–LOPA Methodology
7.2.3.1. Methodology development
Table 7.3
LOPA Incident Scenarios in an LNG Terminal
| No. | Scenarios |
| 1 | LNG leakage from loading arms during unloading. |
| 2 | Pressure increase of unloading arm due to block valve failure closure during unloading. |
| 3 | HP pump cavitation and damage due to lower pressure of recondenser resulting from block valve failed closure. Leakage and fire. |
| 4 | Higher temperature in a recondenser due to more boils off gas (BOG) input resulting from flow control valve spurious full open. Cavitation and pump damage leading to leakage. |
| 5 | Overpressure in tank due to rollover from stratification and possible damage in tank. |
| 6 | LNG level increases and leads to carry over into the annular space of LNG, because operator lines up the wrong tank. Possible overpressure in tank. |
| 7 | Lower pressure in tank due to pump-out without BOG input resulting from block valve failed closure. Possible damage tank. |
7.3. Multiscale Models
7.3.1. Material Failure

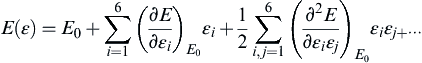

![]()
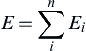

![]()


7.3.2. Corrosion
Table 7.4
Corrosion Inhibitors (Center for Chemical Process Safety [CCPS], 2012)
| Inhibitor | Method of Action | Example |
| Absorption type | Suppresses metal dissolution and reduction reactions | Organic amines |
| Hydrogen evolution poison | Retards hydrogen evolution but can lead to hydrogen embrittlement | Arsenic ion |
| Oxygen scavenger | Removes oxygen from aqueous solution including water | Sodium sulfite, hydrazine |
| Oxidizer | Inhibits corrosion of metals and alloys that demonstrate active–passive transition | Chromate, nitrate, and ferric salts |
| Vapor phase | Blanket gas for machinery or tightly enclosed atmospheric equipment | Nitrogen blanket |