CHAPTER 
Analysing manufacturing operations: quantitative methods
 INTRODUCTION
INTRODUCTION
The purpose of this and the subsequent chapter is to give an insight into some basic numerical techniques that can be used to help solve simple problems that we often encounter within firms. These chapters are not designed to turn you into a statistician or an operational researcher. The chapters are designed to take you through some basic statistical tools and techniques.
This chapter will concentrate on several key techniques that will allow you to assess a range of situations quickly. These are basic mathematical techniques that you will have covered on a quantitative methods course. However, we will demonstrate how they can be used and applied in practice. In business there will be occasions when it important for you to be able to produce graphs, identify relationships in data quickly and be able to see trends. This is why we offer some techniques in this chapter. In addition, we have added an Operational Research section because firms often want to know how to assign resources and work out the best allocation of these key assets. As stated throughout the book, one of the central tasks for operations managers is in making the best use of these resources.
We have tried to take a step-by-step approach that should help you understand how to operate the techniques (even if you don't understand what they are doing!).
 Aims and objectives
Aims and objectives
This chapter will provide you with experience in analysing manufacturing operations, and practice with some tools and techniques for that purpose.
After reading this chapter you will be able to understand the application of the following techniques:
1 Statistical approaches:
![]() Linear functions
Linear functions
![]() Regression and correlation analysis (linear)
Regression and correlation analysis (linear)
![]() Time series analysis (bi-variate)
Time series analysis (bi-variate)
![]() Index numbers.
Index numbers.
2 Operations research approaches:
![]() Assignment modelling.
Assignment modelling.
Whilst these may sound a bit complicated, don't worry – they are actually quite easy to do and useful for being able to produce a quick analysis. It is also worth pointing out that Excel spreadsheets are able to do all of the above techniques very quickly for you.
 STATISTICAL APPROACHES
STATISTICAL APPROACHES
This section will look at the statistical tools and techniques highlighted in the introduction. We will learn to do four key techniques. Table S1.1 should help you decide what techniques you should use and when.
Table S1.1 can be used as a quick reference guide to the techniques and how they are applied to a given problem or set of data. Before going through the techniques, it is worth spending a few minutes to discuss the various data types.
There are basically two types of data that you will come across; bivariate and multi-variate. Although these sound technical, they are actually quite simple; bi- (means two) variate data simply means that you are comparing one variable with another (e.g. sales over time, production output in a given period, the relationship between use of birth control devices and birth rates). A variable is something that you are comparing – i.e. the thing itself. For example, sales will be a variable, and time will be a variable. Often we will put a letter to indicate these variables. Don't get confused by this, you can use the full names or letters as you wish – for example, y = sales and x = time (useful tip: time is always shown on the x axis). Sometimes these relationships will be positive (for example, more time results in greater numbers of sales); sometimes they may be negative (for example, the greater the use of birth control methods, the less births!). The positive and negative relationships are generally reflected in the slope or gradient of the line (linear relationship), i.e. if positive the line slopes up, if negative the line slopes down.
Table S1.1 Statistical tools and techniques
Technique |
Purpose/Focus |
When Used |
Linear functions |
Plotting a straight line. Working out the points of a line, calculating the gradient of a line |
Plotting simple data to understand trends, i.e. growth or declines in sales, deliveries etc. Easy to do on Excel, or just with a paper and pencil! |
Regressions and correlation |
Allows you to make sense of clusters of data. Will allow you to predict (extrapolate) the data and see just how the data is clustered. This technique will also tell you how accurate your prediction is. |
Very useful method, used constantly in industry for predicting trends in data – e.g. sales increases and decreases |
Time series modelling |
Builds on regressions and correlation techniques. Focus is on how data varies over time and the types of variations that are basically split into two: seasonal versus cyclical |
Anywhere where you want to see a time effect or know a time effect – e.g. in marketing for promotions, in purchasing to understand commodity price variation etc. |
Index numbers |
Allows you to be able to scale a range of numbers and then to tell the differences between these numbers |
Purchasing will use the technique to track spends and inflation targets. It will help you make sense of ranges of numbers and to build your own index to track the number changes |
Assignment modelling |
A useful technique that helps with scheduling complex problems. Based on operational research, it will allow you to minimize or maximize a range of constraints |
Used for scheduling. Originally developed for assigning workers to machines, but the use has been extended to a variety of scheduling problems |
Multi-variate data involve more than two variables – e.g. birth control, birth rates and time. This requires more complex techniques, but uses basically the same principles. This chapter will concentrate on only bi-variate (two variables) techniques.
 Linear functions
Linear functions
Basically, a linear function represents a straight line. We often express a straight line in algebraic form. Don't get confused when you see an equation; it is merely a shorthand form. The longhand version of the equation is:
A straight line is described as the start point (known as the intercept), plus a level of increase or decrease (known as the gradient).
In algebraic terms, the following equation is used:
y = a + b(x)
Where the intercept and b(x) is the gradient, this could be positive (i.e. going up) or negative (i.e. going down). You will often see an equation for a line written like this: y = 4x + 6. Immediately you should realize that this is a positive line (i.e. going up), because it has a plus sign. Remember, y means the axis. Plotting a straight line is actually quite easy. First, you only need two points (although you should really go for three to double check). Let's take the equation y = 4x + 6. The easiest way to draw the line is to put in values for x, so for simplicity start with x = 1. The value of y can be found by substituting x into the equation, i.e. y = 4(1) + 6, which will give you 10. This is one point on a line. If you put any other values for x into the equation you will get other points on the line; the logical ones to use are 2 and 3!
Try a few with different numbers and see what results you obtain.
Now let's just summarize how you might do this on a step-by-step approach:
![]() Step 1. Select a few convenient values for x (three points are better than two)
Step 1. Select a few convenient values for x (three points are better than two)
![]() Step 2. For each x value calculate the corresponding y value, using the formula:
Step 2. For each x value calculate the corresponding y value, using the formula:
y =a + b(x)
![]() Step 3. Draw a graph with y (vertical axis) and x (horizontal) axes – always remember x as ‘x marks the spot and therefore it must be on the ground’, and so the vertical axis is the y one!).
Step 3. Draw a graph with y (vertical axis) and x (horizontal) axes – always remember x as ‘x marks the spot and therefore it must be on the ground’, and so the vertical axis is the y one!).
![]() Step 4. Plot the pairs of x and y values on the graph.
Step 4. Plot the pairs of x and y values on the graph.
![]() Step 5. Join up the points to see the line.
Step 5. Join up the points to see the line.
That's all there is to it!
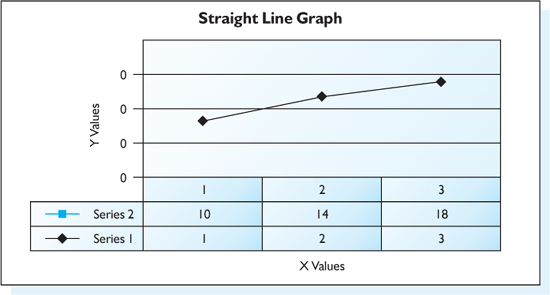
Here is a worked example to help you. Plot the straight line corresponding to the function y = 4(x) + 6. Choosing the values x = 1, 2 and 3, the following calculations are made:
For x = 1, y = 4(1) + 6 = 10
For x = 2, y = 4(2) + 6 = 14
For x = 3, y = 4(3) + 6 = 18
Now all we have to do is to plot this onto a graph and join up the dots to make a straight line (Figure S1.1).
Figure S1.1 Straight-line graph.
There are a couple other little tricks that you might want to think about. First, you are not always given the equation in a straightforward form and so you may need to work out the gradient of the line for yourself. Second, you might need to work out the equation for the line. Let's now work through how you would do each of these things – if you have understood things so far, this next bit will be easy!
 Determining the value of a gradient of a given line
Determining the value of a gradient of a given line
First, if a line is given (without its equation), the procedure for calculating the gradient is quite easy:
![]() Step 1. Identify any two points on the line (just read off the x and y coordinates).
Step 1. Identify any two points on the line (just read off the x and y coordinates).
![]() Step 2. Calculate the vertical numerical difference between the points, and the horizontal differences between the points.
Step 2. Calculate the vertical numerical difference between the points, and the horizontal differences between the points.
![]() Step 3. Gradient = vertical numerical differences/horizontal numerical differences.
Step 3. Gradient = vertical numerical differences/horizontal numerical differences.
Having looked at straight-line functions, let's now move on to something a little more detailed.
 Regression analysis
Regression analysis
Regression is a term used to describe relationships between variables – in our case between two variables, as it is bi-variate data. The regression technique is very powerful and can also be used to look at the relationships between multiple variables. This is known as multi-variate regression, and can be conducted using standard statistical packages such as SPSS and MiniTab. However, for our purposes we are going to look at linear regression, which by definition will only use two variables and will only look at linear relationships (i.e. where a straight line can be drawn) as opposed to non-linear or polynomial relationships, which would model much more complex data.
This section will discuss how you can calculate a regression line. In practice, it is very easy to do this using any mainstream spreadsheet programme. However, it is important to understand the basics of how the technique works, because this will also allow you to understand if you have done anything wrong!
 Regression and its uses
Regression and its uses
Imagine you are a consultant working in a purchasing department whose input into business decision-making process is welcomed within the firm. The Purchasing Manager believes that by working more closely with suppliers, subsequent delivery performance will improve. His idea of working more closely means visiting suppliers on a regular basis to discuss business issues, and also to show an interest in the firm. As a consultant you want to know if his assumption is true (as it will obviously have a cost and possibly a benefit, i.e. the cost of visiting vs. the benefit of improved delivery performance). You need to understand if there is a relationship between the amount of visits and delivery performance. If a relationship between these two variables were found, you might expect to find that the more visits that you make to a supplier the better the delivery performance. We could also go further than this and ask, if we made 10 visits, by how much more would delivery performance improve?
This question can be answered, and demonstrates one of the most useful aspects of regression, which is being able to predict (or extrapolate) the trend of the data based on previous data. In effect, it is the ability to estimate the value of one of the variables, given the value of the other. Regression relationships are also useful for comparing against other firms – e.g. advertising expenditure vs. turnover could be compared against other firms. Consultants refer to this cross comparison as ‘benchmarking’, which was discussed in Chapter 10.
 Standard methods of obtaining a regression line
Standard methods of obtaining a regression line
The regression line (which is also known as the line of ‘best fit’) is a straight line that has the closest fit to the data points you have gathered from your data set. This means it is the line that cuts through the middle of the data points (this will become clearer shortly). This line can be calculated in three ways:
1 Inspection: This method is the simplest, and consists of plotting a scatter diagram and drawing the line that most suitably fits the data points. The main disadvantage of this method is that different people would probably draw different lines using the same data, just because they would see the data differently! To make it a little more scientific you could plot the average, or mean, point of the data and ensure that the line passes directly through it.
2 Semi-averages: This technique consists of splitting the data into two equal groups, plotting the mean points for each group and then joining them together to get a straight line. This again is quite quick and easy, but because of the averaging effect it may mean that the line is not an accurate fit. The problem then comes when you attempt to predict with the line (or extrapolate) – any errors in the line fitting will be exaggerated as the line is extended, which will mean that your predictions become difficult to substantiate.
3 Method of least squares. This method is considered as the standard method for obtaining a regression line. Your calculator or spreadsheet will use this method to obtain the ‘line of best fit’. This method will calculate the route of the line by squaring the points along the line to find the narrowest path through the data points. Think of it this way; as you square a number it becomes bigger, which means that the distance between the points becomes smaller, and the line can then be fitted through the space much more accurately. The general rule is:
. . . the least squares regression line of y on × is that line for which the sum of squares of the vertical deviations of all the points from the line is least.
The next section will concentrate on the method of least squares, as this is the most common method used in practice. We will have a look at some of the mathematics that sits behind it. Try not to worry too much about the complex looking formulae; simply think of them as a list of instructions. All you have to do is put the relevant numbers into the equation to read off the results.
There is one other main point to note before we look at the equation. Because we are dealing with bi-variate data, the line is referred to as a y on x regression line. This means that y is the dependent variable and x is the independent variable. This might sound a bit confusing. So think of it like this – the y (vertical) axis is always the thing that you are trying to predict, and x is the variable that will always be there.
 Formulation for obtaining the y on x least squares regression line
Formulation for obtaining the y on x least squares regression line
The line that you are deriving is basically the straight line that we discussed in the first section – in other words, y = a + b(x). However, to find the values of a and b you will need to use the following formulae (or lists of instructions). This first formula will give you the value for b within the y = a + b(x) equation; n is the number of observations.
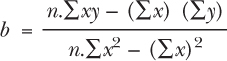
At first glance this may look complicated, but when we go through the example the application of the formula will become clear. This next formula will give you the value for ‘a’. Note that you must work out ‘b’ first, as you need the result to put into the next equation.
The value for a is calculated as follows:
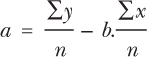
Now all you have to do is to work out the values for each, put them into the equation and work them through. Let's work through an example to see how to do it.
Example
Assume that you are a consultant and have been commissioned by the Director of Production to help her with a small problem. She is concerned about the cost of maintaining her machines, and she also worried about their age. She wants to know if there is a relationship between the cost and age of the machines. Furthermore, she would also like to know what would be the predicted maintenance costs of a machine that is 40 months old. (Remember that regression lines can be positive and negative, although this one is very likely to be positive – i.e. the older the machine, the more it will cost).
You set off and look at 10 machines, and collect cost and maintenance data for each. Now remember, you must first think about what you are trying to predict – i.e. dependent (y) vs. independent (x) variables. In this case, as in most, time is independent (i.e. it is marching on regardless) and therefore that must be the (x) variable. Consequently, cost must by the y axis! You could also think, ‘what am I trying to predict – time or cost?’ The answer is cost; therefore y is cost as this is dependent. The data from your observations are as follows:

(Note: The number of observations (in our example, machines) is always referred to as ‘n’).
Having decided on the x and y variables, you now need to construct a table to conduct the calculations (note a spreadsheet will do all this for you). You then simply take the elements for the formula and do the calculations, making sure you don't rush this bit!
x |
y |
xy |
x2 |
5 |
190 |
950 |
25 |
10 |
240 |
2400 |
100 |
15 |
250 |
3750 |
225 |
20 |
300 |
6000 |
400 |
30 |
310 |
9300 |
900 |
30 |
335 |
10050 |
900 |
30 |
300 |
9000 |
900 |
50 |
300 |
15000 |
2500 |
50 |
350 |
17500 |
2500 |
60 |
395 |
23700 |
3600 |
Now you need to total them all up. Remember that ∑ means summation, or ‘sum of’, which simply means add it all up. So anytime you see this sign in front of anything, it means you must add all the values to give a total. The totals for the above are:
Totals |
y |
xy |
x2 |
300 |
2970 |
97650 |
12050 |
Now simply list the elements so that you can see which bits go into which parts of the equation:
Σx = 300
Σy = 2970
Σxy = 97650
Σx2 = 12050
All you then have to do is put these numbers back into the formula:
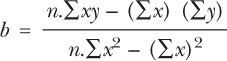
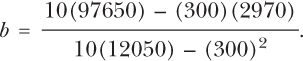
This will give you
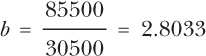
You then need to do the same for ‘a’, using the formula:
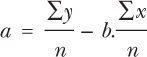
which will give you:
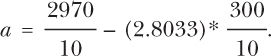
This will give you:
a = 297 − 30(2.8033) = 212.90
Therefore, the least squares regression line on age is y = 212.90 + 2.8033(x). You can now use this equation to calculate your predicted maintenance cost by inserting the figure 40 (for time) instead of the ‘x’ and multiply through. This will give you the total of £325. In other words, it will cost £325 to maintain the machine after 40 months.
As you can see, this is relatively mechanical. You should try this by longhand, and then using a spreadsheet programme. You could also try plotting the data in a scatter diagram; substitute two figures for x and then draw the regression line through the data.
Here is an example for you to work through:
A large company's Sales Manager has tabulated the price (£) against engine capacity (cc) for 10 models of car available for salesmen as follows:

Obtain the least squares regression line of price on engine capacity. Discuss how you might use the regression line to help you in making management decisions. What are the advantages and disadvantages of your model?
 Correlation techniques
Correlation techniques
Correlation is a technique that is used to measure the strength between two variables. It is often used in partnership with regression, as it will allow you to understand how well your line fits, plus how much of the data your line explains. This is very important for understanding the accuracy of the prediction. There are two well-known techniques for conducting correlation analysis; these are Rank correlation and the Product moment correlation. There are also other correlation methods, such as the coefficient of determination and various measures of dispersion. For our purposes, we will concentrate on the Product moment correlation. You should refer to a statistics textbook for some of the more complex methods.
The purpose of regression is to identify a relationship for a given set of bi-variate data; however it does not give any indication of how good this relationship might be – i.e. how well the line fits the data. This is where correlation analysis steps in. The better the correlation the closer the data points are to the line, and the more accurate the predictions. Correlations are given from +1 to –1; i.e. the closer to 1 you get the better the fit, and therefore the more accurate your line. A positive correlation of +1 would indicate a line sloping upwards where the data and the line fit exactly, a correlation of –1 would indicate the same thing, although the line would be pointing downwards – e.g. in the relationship between birth rate and use of condoms, the more condoms used, the lower the birth rate! Remember that a correlation of 0 would signify no relationship. To give you an idea:
. . . correlation is concerned with describing the strength of the relationship between two variables by measuring the degree of ‘scatter’ of the data values.
The basic rule is that the less scattered the data, the stronger the correlation. Again, don't be put off by the formula; it is quite easy when you start substituting variables into the equation.
The Product moment coefficient is known as r, and it is derived by using the following formula:
Using the example from the regression section, let's look at the correlation coefficient for machines to see how accurate our forecast was. The data are as follows:

We calculate the data in the normal way, using a similar tabular approach to that used above; however, notice that we have a new column in this table, y2.
x |
y |
xy |
x2 |
y2 |
5 |
190 |
950 |
25 |
36100 |
10 |
240 |
2400 |
100 |
57600 |
15 |
250 |
3750 |
225 |
62500 |
20 |
300 |
6000 |
400 |
90000 |
30 |
310 |
9300 |
900 |
96100 |
30 |
335 |
10050 |
900 |
112225 |
30 |
300 |
9000 |
900 |
90000 |
50 |
300 |
15000 |
2500 |
9000 |
50 |
350 |
17500 |
2500 |
122500 |
60 |
395 |
23700 |
3600 |
156025 |
This table gives the following output when the columns are totalled:
Σx = 300
Σy = 2970
Σxy = 97650
Σx2 = 12050
Σy2 = 913050
Now all we do is substitute it into the equation as before:
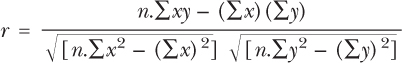
(Note: when a squared sign is outside of the brackets you have to square the numbers inside – i.e. (∑y)2 is the sum of all the y values squared, as opposed to y2, which has already been calculated.)
So, substituting the values above into the equation will give you the following:
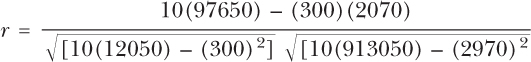
When you work this through, you will get:
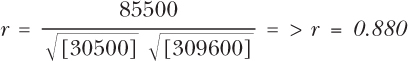
The final correlation is 0.88, which would indicate a good fit with the data. As a rule of thumb, anything above 0.75 (plus or minus) would indicate a good fit.
Having taken you through the basics of correlation and regression, we will now move on to look at some other statistical techniques that take this work as their basis.
 Time series modelling
Time series modelling
A time series looks at the movement of data of over time and attempts to find a trend within the data. This trend can then be used to predict future events. Time series is a very useful technique, and is employed regularly as part of general business practice. Time series models range from the very simplistic to the very complex. On the simple end of the scale, the models will look at extrapolating a data range (for example using multiple regression); this can be achieved by extending a line of best fit through the data. Other methods included calculating semiaverages and moving averages. These methods are relatively simple, and we will explore them briefly.
As mentioned, the basis of time series is to identify trends; the power of time series is being able to model these trends. In the basic form we can categorize these trends into two distinct types: seasonal (within a year) and cycle (yearly or greater than a year). This section will explore how to identify and calculate these types of models. These trends can also move in two ways; they are said to be either additive or multiplicative (these terms will be explained later). The more complex time series models will be multi-variate, and will combine seasonal and cycle as well as error movements, these are known as Arithmetic Integrated Moving Average (AriMA) models. This technique combines multi-variate regression analysis with time series models. However, this is too complicated for us, so we will concentrate on the more simple approaches. If you are interested in developing your skills in time series modelling you should refer to some specialist textbooks on the subject.
 Techniques for finding the trend
Techniques for finding the trend
There are three techniques for finding the trend within data:
1 Least squares regression. This method was introduced in the last section, and looked at ways of extending (extrapolating) a line through a series of data.
2 Semi-averages. This is a very simple technique which, as its name suggests, involves calculating two averages through the data and plotting a line.
3 Moving averages. This is the most commonly used method for identifying a trend, and involves the calculation of sets of averages.
Each method will be discussed in turn, with an example.
 The method of least squares regression
The method of least squares regression
This technique will only work if the data is bi-variate (two variables), i.e. something against time. Remember the rule of dependent and independent variables, therefore time will be independent (x) versus something that you want to predict (y). To develop this model, the steps are as follows:
1 Take the physical time points as values (you could code them 1, 2, 3, . . . 10 etc.); remember these will be independent (x).
2 Take the data values themselves as values of the dependent variable (y) and match them to the time points.
3 Calculate the least squares regression line of y on x, y = a + b(x).
4 Translate the regression line as t = a + b(x), where any given value for the time point x will give a corresponding value for t.
This process for developing t is exactly the same procedure that we carried out in the last section. The only difference is that once you have got your y on x line, you substitute in all the time values to get your trend line. In other words, you put the coded time points into the x bit of the equation.
Example
You have been asked to calculate a trend for the distribution of airline passengers against time. The airline has calculated data of 12 equal time points (x) and the number of passengers that have travelled (y). The time slots refer to quarters, i.e. 1 = year 1 quarter 1; 10 = year 3 quarter 2).
The data are shown in the following table.
x |
y |
xy |
x2 |
Trend (t) |
1 |
2.2 |
2.2 |
1 |
4.11 |
2 |
5.0 |
10 |
4 |
4.28 |
3 |
7.9 |
23.7 |
9 |
4.45 |
4 |
3.2 |
12.8 |
16 |
4.62 |
5 |
2.9 |
14.5 |
25 |
4.79 |
6 |
5.2 |
31.2 |
36 |
4.96 |
7 |
8.2 |
57.4 |
49 |
5.13 |
8 |
3.8 |
30.4 |
64 |
5.30 |
9 |
3.2 |
28.8 |
81 |
5.47 |
10 |
5.8 |
58 |
100 |
5.64 |
11 |
9.1 |
100.1 |
121 |
5.81 |
12 |
4.1 |
49.2 |
144 |
5.98 |
Total |
60.6 |
418.3 |
650 |
|
Putting the regression line together you will have b = 0.17 with a = 3.94. Therefore the regression line for the trend is t = 3.94 + 0.17(x). The time points can now be substituted into the regression line to give the trend line. This has already been calculated in the above table; now all you have to do is to plot the trend line on a scatter diagram.
 The method of semi-averages
The method of semi-averages
This is a very simple method of obtaining a line and, although it is not as accurate as the least squares method, it will provide you with a quick result. It simply involves calculating two averages, which will give you two points on a graph; you then draw a line through these two points to produce your trend line. (Remember, with these two points you could work backwards and construct the equation for the line using the work on linear functions; this would then give you a more accurate predictor.)
This method will be demonstrated by using an example. Suppose you were asked to work for a gallery and to estimate the trend of customers through the exhibition based on the first 2 weeks. The following data set has been recorded:
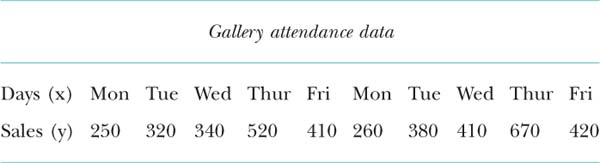
You are required to obtain the semi-average trend line for this data. (Note that the data is time ordered, which is what you need for time series data. If it is not given to you in this form, then just simply order it so that it makes sense).
![]() Step 1. Split the data into two groups, an upper and a lower group. The easiest way to do this is to split it into weeks 1 and 2.
Step 1. Split the data into two groups, an upper and a lower group. The easiest way to do this is to split it into weeks 1 and 2.
![]() Step 2. Find the mean of each group (add them up and divide by n – in this case 5).
Step 2. Find the mean of each group (add them up and divide by n – in this case 5).
The mean of the lower group (L) is 1840/5 = 368
The mean of the upper group (U) is 2140/5 = 428
![]() Step 3. Plot, on a graph, each mean against an appropriate time point. (Note that you could also code the time points 1 to 10 if you wanted.) An appropriate time point would be the mean of the time points that you are looking at i.e., L against Wednesday of week 1 and U against Wednesday of week 2.
Step 3. Plot, on a graph, each mean against an appropriate time point. (Note that you could also code the time points 1 to 10 if you wanted.) An appropriate time point would be the mean of the time points that you are looking at i.e., L against Wednesday of week 1 and U against Wednesday of week 2.
![]() Step 4. Now all you do is draw a line that connects these two points. This gives a trend line through the data, and you can now read off of the points and extend the line for future predictions.
Step 4. Now all you do is draw a line that connects these two points. This gives a trend line through the data, and you can now read off of the points and extend the line for future predictions.
Example
Now attempt this example – the data set is from the least squares method, so you should be able to double check your calculations! Using the method of semi-averages, calculate the trend line for this data set.
You work for a large airline company and have been asked to examine the trends in flying so that the airline can predict the impact on its operations and see if it needs to increase (or indeed decrease) capacity in any area. The following data have been obtained regarding UK outward airline passengers.

When you are confident with this technique, move on to the next section.
 The moving average
The moving average
This is the most common method of calculating a time series trend, and involves calculating a set of averages, each one corresponding to a trend (t) value for a time point of the series. These are known as moving averages, since each average is calculated by moving from one overlapping set of values to the next. The number of values in each set is always the same, and is known at the period of the moving average. The period is simply the time period over which the averages are obtained, and will depend on the data. For example, the following data set has been calculated for moving averages of period 5. There are a few things to notice here. First, you will not obtain a moving average for the first or last data point (this is a weakness of the technique). This is because these points are needed for the calculation of the average, which by definition will be in the middle of the data points. Have a look at the following table.
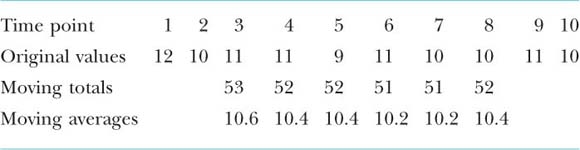
The first total, 53, is formed from adding the first five items (time points 1–5). That is, 12 + 10 + 11 + 11 + 9 = 53. Similarly the second total is derived from adding the next five time point values (2–6), and then time points 3–7 and so on. This process will give you the moving totals of the data points. The averages are then obtained by dividing each moving total by 5, because you are working on a 5-period average. This will give you the moving average total for the data. You can then plot this on a graph; remember time (x) against y data (predictor). A simple definition is:
Moving averages (of period n) for the values of a time series are arithmetic means of successive and overlapping values, taken n at a time.
There are two rules for you to remember when working with moving average data:
1 The period of the moving average MUST coincide with the natural cycle of the series – e.g. if the data were in quarters then the period would be 4, if you were looking at monthly sales then the period would be 12. If a supermarket were open 7 days a week and you were looking at the trend over 2 weeks, what would be the period? The answer is 7, as you are looking at the average of the week's takings over 2 weeks. 7s will give you the average.
2 Each moving average trend must correspond with a relevant time point for the values being averaged. These can always be determined as the median of the time points of the values being averaged. For moving averages with an odd numbered period (3, 5, 7, etc.) the relevant time point is that corresponding to the second, third, fourth value etc. However, if the time points are even there is no obvious point to place the average. Therefore we have to employ another technique, which is known as centring, and we'll guide you on this.
Centring a moving average series
Remember, this technique only applies when calculating moving averages of data that have an even period point (i.e. 4, 6, 8 etc.); this is because the resulting moving average has to be placed in between two corresponding time points. As an example, the following data set has a 4-period moving average calculated, and shows where the calculated average should be placed.
As you can see from the data, the averages are placed between the time points – e.g. 52 is placed between 2 and 3 and so on. The placing of these averages in the mid-time points will make it very difficult for plotting trend lines. We will need to align these averages to the time points so that they can be plotted, and this is the concept of centring. This a simple process, where the calculated averages are themselves averaged in successive overlapping pairs; hence the term centred moving averages. Taking the above data set, centring the averages will give the following:
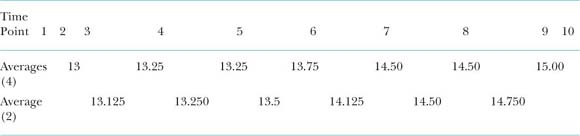
You can see that by averaging the mid-data points we have centred each data point against a time value – i.e. 2, 4, 5, etc. You can now easily plot this line on a graph.
Example
Now it is your turn. Try to create a centred moving average trend line using the following data set for aircraft passengers.

 Comparison of techniques
Comparison of techniques
Having completed the examples, you will see that each technique gives a slightly different result. This demonstrates that there is no unique trend for a set of data values; the trend will depend on the sophistication of the technique that you are using. Semi-averages, although very simple to apply, is probably the weakest of the techniques, due to the fact that only using two data points to plot a line can lead to ambiguity. In addition, it assumes a strictly linear function! The least squares method, whilst more sophisticated and accurate, still assumes a linear relationship – i.e. it will ignore any seasonality within the data set. Finally, the method of moving averages is the most widely used technique for obtaining a trend line. If the period of the averages is chosen appropriately it will show the true nature of the trend, whether linear or non-linear. The disadvantage of this technique is that there are no beginning and end values obtained for the trend cycle.
 Seasonal variation and forecasting techniques
Seasonal variation and forecasting techniques
This concept is the basis of time series modelling. Seasonal (or short-term cyclical) variations are present in many time series. For example, you could be looking at trends in fashion, sportswear, buying behaviour, price movements, consumer numbers, sales figures etc.
Seasonal values or factors are generally expressed as deviations, i.e. plus or minus from the underlying trend – for example, inflation has risen by 1 per cent above the trend, or oil prices have fallen 5 per cent below the trend, etc. We can therefore define seasonal as:
A seasonal variation gives an average effect on the trend that is solely attributable to the ‘season’ itself. They are expressed in terms of deviations from the trend.
Having established the need for this type of work, let's go onto examine how we can calculate the seasonal variation component.
 Techniques for calculating seasonal variation
Techniques for calculating seasonal variation
Remember, we started with y = a + b(x) for our straight line. We then refined it to read t = a + b(x) in order to give us a trend line. We will now need to add a few more components to give us the seasonal variation. The new model will take the form:
y = t + s + r
where t is the trend, s is the seasonal variation and r is the residual or error (the bit we can't explain). In the more complex models the residual factor is also modelled; this is something we will not worry about! Here is how you calculate the seasonal variation:
![]() Step 1. Calculate, for each time point, the value of y – t (i.e. difference between the value and the trend – note, this could be plus or minus).
Step 1. Calculate, for each time point, the value of y – t (i.e. difference between the value and the trend – note, this could be plus or minus).
![]() Step 2. For each season in turn, find the average of all the y – t values.
Step 2. For each season in turn, find the average of all the y – t values.
![]() Step 3. If the total of the averages differs from zero, adjust one or more of them so that their total is zero (you'll see how to do this in the example, although it is generally a matter of common sense).
Step 3. If the total of the averages differs from zero, adjust one or more of them so that their total is zero (you'll see how to do this in the example, although it is generally a matter of common sense).
Example
Let's work through an example so that you can see step-by-step what you have to do. Assume that you have been given a set of production figures and are trying to see the trend in seasonal variations. The following data set has been collected.
Step 1: Calculate y – t, i.e. the trend differential. Do this and put it in a row below.
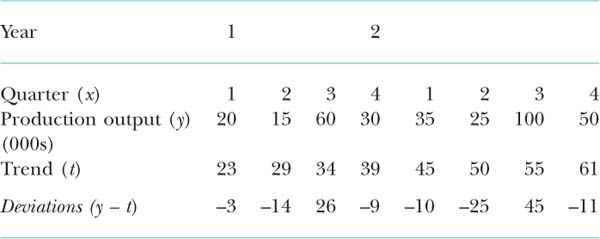
Step 2: for each season in turn you now need to calculate the (y – t) averages.
Quarter |
1 |
2 |
3 |
4 |
Year 1 |
–3 |
–14 |
26 |
–9 |
Year 2 |
–10 |
–25 |
45 |
–11 |
Totals |
–13 |
–39 |
71 |
–20 |
Averages |
–6.5 |
–19.5 |
35.5 |
–10.0 |
Step 3: you now need to sum the averages and see if they add up to zero. In this case they do not. They come to –0.5, and therefore we will need to add on an extra 0.5 to one of the values. In order to minimize the amount of error, add 0.5 on to the largest value (which will give proportionately the smallest change). Therefore readjust 35.5 to read 36, so that they now sum to zero. This will give us the following amended table.
Averages |
–6.5 |
–19.5 |
36.0 |
–10.0 |
The interpretation of the figures is that the average seasonal effect for quarter 1, for instance, is to deflate the trend by 6.5 (000s) units, and that for quarter 3 it is to inflate the trend by 36 (000s) units.
 Seasonally adjusted time series
Seasonally adjusted time series
Once we have these data we can use them to adjust the actual trend itself, in the light of seasonal variations. This is achieved by subtracting the appropriate seasonal figure from each of the original time series values. This can be shown in the model y – s. The effect of this operation will be to smooth away seasonal fluctuation, leaving a clear view of what might be expected had seasons not existed. This effect is shown in the following data table.
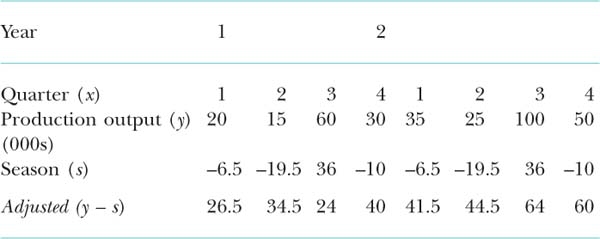
Now we can see the trend without the seasonal component. It is common practice to adjust trends seasonally. You will often read in the newspaper or see on the TV examples of this technique, such as inflation referred to as actual and seasonally adjusted.
Seasonally adjusted time series values are obtained by subtracting the appropriate seasonal variations from each of the original time series values (y – s).
Example
Now it's time for you to attempt a problem! Use the data regarding UK outward airline passengers given below, find the seasonal variations, and then plot the time series on a graph and adjust for any seasonal variance. Plot the new seasonally adjust trend line and comment on the differences.

 TECHNIQUES FOR FORECASTING
TECHNIQUES FOR FORECASTING
One of the main uses of time series is to develop forecasts from the data series, and this is sometimes referred to as ‘projecting the series’. This projection of the series is, however, only as good as the historical data on which it is based, and also on the accuracy and complexity of the model that has been created – no one can predict the future, but we can (under certain assumptions) make a guess regarding what might happen based on past events.
Forecasting models can be generalized into two approaches; additive and multiplicative. We will concentrate on the simpler of the two, the additive model, which is given by the following:
Time series forecasting can be attempted using the simple additive model:
yest = test + s
where:
yest = Estimated data value
test = Estimated (projected) trend value
s = Appropriate seasonal variation value.
This model does not make a provision for residual ‘r’, because residual values are assumed to average out at zero.
In order to see how this works, let's try an example.
Example
Forecast the values for the four quarters of year 4, given the following information calculated from a time series. Assume that the trend in year 4 will follow the same pattern as in years 1 to 3.
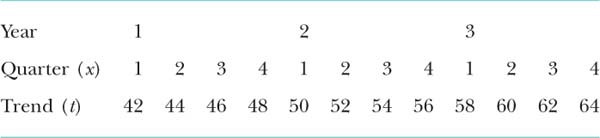
S1 = seasonal factors for quarter 1 = –15; S2 = –8; S3 = +6; S4 = +17.
![]() Step 1. Estimate trend values for the relevant time points. Trend for year 4, Q1 = t4,1 = 66 Similarly, t4, Q2 = 68, t4, Q3 = 70 and t4, Q4 = 72.
Step 1. Estimate trend values for the relevant time points. Trend for year 4, Q1 = t4,1 = 66 Similarly, t4, Q2 = 68, t4, Q3 = 70 and t4, Q4 = 72.
![]() Step 2. Identify the appropriate seasonal factors. The seasonal factors for year 4 are taken as the given seasonal factors – that is, seasonal factor for year 4, Q1 = S1 = –15 etc.
Step 2. Identify the appropriate seasonal factors. The seasonal factors for year 4 are taken as the given seasonal factors – that is, seasonal factor for year 4, Q1 = S1 = –15 etc.
![]() Step 3. Add the trend estimates for the seasonal factors, giving the required forecasts.
Step 3. Add the trend estimates for the seasonal factors, giving the required forecasts.
Forecast for year 4, Q1 = t4,1 + S1 = 66 – 15 = 51;
Forecast for year 4, Q2 = t4,2 + S2 = 68 – 8 = 60;
Forecast for year 4, Q3 = t4,3 + S3 = 70 + 6 = 76;
Forecast for year 4, Q4 = t4,4 + S4 = 72 + 17 = 89.
Forecasting the trend line is relatively straightforward given a linear trend; if linearity does not exist, you could use a moving averages trend line to extend the series.
 INDEX NUMBERS
INDEX NUMBERS
Index numbers are constantly used by a variety of people in organizations to make decisions. These numbers allow us to make comparisons of trends over a period of time. They convert series of numbers to linear scales, which can be extremely useful in helping us to make quick and accurate comparisons of data sets.
 Definition of an index number
Definition of an index number
An index number measures the percentage change in the value of something (for example, an economic commodity such as oil or sugar etc.) over a period of time. It is always expressed in terms of base 100.
 Examples of index numbers
Examples of index numbers
In order to understand index numbers, let's work through a few simple examples. First, we will look at a price increase index. Suppose that the price of a standard box of ballpoint pens was 60p in January and rose to 63p in April. What is the percentage increase?
You would calculate this by taking the second number (N2) and subtracting the first number (N1); then divide by N1 and multiply by 100 to give you a percentage.
The equation to give percentage change is:
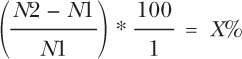
In other words, the price of ballpoint pens rose by 5 per cent from January to April. To put this into an index number form, the 5 per cent increase is added to the base of 100, giving 105. This is then described as follows:
The price index of ballpoint pens in April was 105 (January + 100)
which:
![]() Gives the starting point (January) over which the increase in price is being measured.
Gives the starting point (January) over which the increase in price is being measured.
![]() Emphasizes the basis value (100) of the index starting point.
Emphasizes the basis value (100) of the index starting point.
Having seen that this is quite an easy process, let's look at an example of a decreasing index. If the productivity of a firm (measured in units of production per man day) decreased by 3 per cent over the period 1998–2000, how would this be shown using the index number method?
First, take the percentage decrease of 3 per cent (which has already been calculated for you) and then subtract this from the base index 100 (i.e. 100 – 3); this will give you an index number of 97. If you were asked to describe this index shift, you would say:
The productivity index for the company in 2000 was 97 (1998 = 100).
Again, this statement gives the year of the index plus the base year. The base year is the year in which the index started, or the year from which conversions are currently being made. This is because sometimes indexes are re-indexed to a new base year, especially when there has been a massive movement in the index itself.
 Notation
Notation
In order to be able to describe some of the more complicated index processes it is necessary to use some ‘shorthand’, and this is referred to as notation. It is convenient, particularly when giving formulae for certain types of index numbers, to be able to refer to an economic commodity at some general time point. Price and quantities (since they are commonly quoted indices) have their own special letters, p and q respectively. In order to bring in time, the following standard convention is used:
P0 = Price at base time point
Pn = Price at some other time point
Q0 = Quantity at base time point
Qn = Quantity at some other time point.
Using the ballpoint pen example, the time period ‘0’ was January, and the time period ‘n’ was April; P0 = 60 and Pn = 63. It is just a matter of substituting the words for letters.
 Index relatives
Index relatives
As well as index numbers, there are also index relatives. These are sometimes just called ‘relatives’, and this is the name given to an index number that measures the change in a simple distinct commodity. A price relative was calculated in the ballpoint pen example, and a productivity relative was calculated in the second example. There is, however, a more direct way of calculating relatives, and this is given by the following formulae.
Price relative index. You should use this formula to calculate the relative price movement of an index from its base starting point:
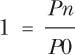
Quantity relative index. You should use this formula to calculate the relative quantity movement of an index from its base starting point:
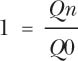
 Time series of relatives
Time series of relatives
It is often necessary to see how the values of an index relative change over time. Given the values of some commodity over time (i.e. a time series), there are two distinct ways in which relatives can be calculated: fixed and chain-based relatives.
Fixed-based relatives
Here, each relative is calculated based on the same fixed time point. This approach can only be used when the basic nature of the commodity is unchanged over the whole period. Fixed based relatives are used for comparing ‘like with like’.
Chain-based relatives
In this case, each relative is calculated with respect to the immediately preceding time point. This approach can be used with any set of commodity values, but must be used with the basic nature of the commodity changes over the whole time period.
 OPERATIONAL RESEARCH TECHNIQUES
OPERATIONAL RESEARCH TECHNIQUES
 Assignment modelling
Assignment modelling
The use of assignment modelling is widespread within, business. Although it is often performed using computer software, it is also very easy and quick to do manually. Assignment modelling has its routes in linear programming, and it therefore has the aim of finding ‘optimal solutions’ to problems that either maximize or minimize. Assignment models generally focus on minimizing cost or, to put it another way, maximizing value. They can come in all shapes and sizes, and there are some exercises later in the book for you to practise. The trick with learning this technique is simply to be methodical. You do not need to have an advanced understanding of mathematics, but you do need to follow the method.
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
8 |
7 |
9 |
9 |
J2 |
5 |
2 |
7 |
8 |
J3 |
6 |
1 |
4 |
9 |
J4 |
2 |
3 |
2 |
6 |
Now simply follow this methodology:
Step 1: In the first row of numbers, find the smallest number in the row, and write it at the right of the row; repeat this for all the other rows. Matrix 1 should now look like this:
Men/jobs |
M1 |
M2 |
M3 |
M4 |
Smallest No |
J1 |
8 |
7 |
9 |
9 |
7 |
J2 |
5 |
2 |
7 |
8 |
2 |
J3 |
6 |
1 |
4 |
9 |
1 |
J4 |
2 |
3 |
2 |
6 |
2 |
Step 2: Make a new matrix from Matrix 1 and call it Matrix 2. Create the new matrix by subtracting the row minimum (i.e. 7 for row 1) from each number in that row. You should then do the same row for row. So, in row number 2, you will subtract the number 2 from everything, for row 3 it will be the number 1, and for row four it will be? (Yes, that's correct; 2 from everything).
This will give you Matrix 2, which will look like this.
Matrix 2
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
(8 – 7) 1 |
(7 – 7) 0 |
2 |
2 |
J2 |
3 |
0 |
(7 – 2) 5 |
6 |
J3 |
5 |
0 |
3 |
8 |
J4 |
0 |
1 |
0 |
(6 – 2) 4 |
Step 3: Find whether the matrix will give a complete basis for making the optimum assignment of men to jobs by first picking out a pattern of zeros in Matrix 2 in such as way that no row or column (in the pattern) contains more than ONE zero. In order to help you, identify this pattern by putting a square around or highlighting each zero selected. In many cases, including this one, there is more than one pattern of ‘squared’ zeros. Any one of these patterns is acceptable for this step. In this particular case, the pattern of zeros is easily found by a case of trial and error. Here is an example of trying to find the pattern:
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
1 |
0 |
2 |
2 |
J2 |
3 |
X |
5 |
6 |
J3 |
5 |
X |
3 |
8 |
J4 |
0 |
1 |
X |
4 |
(Note: J4 row has two zeros, so just choose one – in this case, M1.)
Step 4: Starting with the matrix constructed in Step 3 (Matrix 2), examine each row until one is found that only has one zero. Make a square or highlight that zero. If there are any other zeros in the same column, put an X through them. Then repeat this process until every row has just one zero highlighted.
Step 5: Now examine the columns until one is found that has only one unmarked zero. Make a square or highlight it, and put an X through any other zeros in the same row. Repeat until all the columns have been examined. In this example, the first column is the only one with just one zero in it (M3 has been crossed out!). If the result of Step 3 is a pattern of zeros with exactly one highlighted zero in every row and column, then the matrix is an optimal solution. In this particular case, Matrix 2 is not optimal. If it were optimal, you could skip steps 5 to 10.
Step 6: In Matrix 2, write the smallest number in each column under the column (note that a minimum number can be a zero as well as any other number).
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
1 |
0 |
2 |
2 |
J2 |
3 |
X |
5 |
6 |
J3 |
5 |
X |
3 |
8 |
J4 |
0 |
1 |
X |
4 |
Smallest no. |
0 |
0 |
0 |
2 |
Step 7: Perform the same operations on the columns that you performed on the rows in Step 2. This will form a new Matrix 3. Check Matrix 3 for the same rule: there is at least one zero in each column, which is as it should be!
Matrix 3
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
(1 – 0) 1 |
0 |
2 |
(2 – 2) 0 |
J2 |
3 |
X |
5 |
(6 – 2) 4 |
J3 |
5 |
X |
3 |
6 |
J4 |
0 |
1 |
X |
2 |
Step 8: Repeat Steps 3 to 7 to see if Matrix 3 is optimal; here it is not!
Step 9: Now put a tick against each row that has no highlighted zero in it – in this case, row 3. Now do the same process for the column that has a zero in a ticked row. The matrix should now look like this:
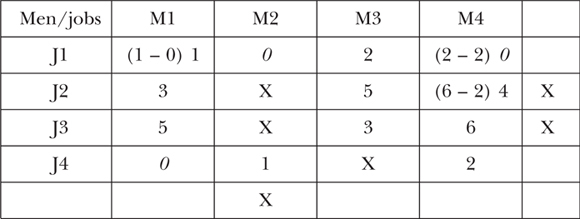
Step 10: Make a tick mark at the right of each row that has a highlighted zero in a ticked column.
Step 11: Draw line through all un-ticked rows and all ticked columns (tip: the number of lines should be the same as the number of highlighted zeros).
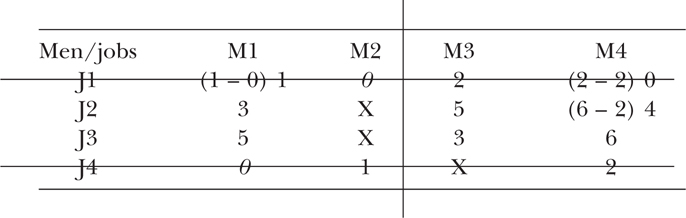
Step 12: Start to form a new Matrix 4. If a number in the previous matrix has only one line through it, copy it onto the same position in Matrix 4. Repeat every number in Matrix 3 that has just one line through it.
Step 13: Find the smallest number in Matrix 3 with no line through it (in our example, this is the number 3).
Step 14: For each number in Matrix 3 with no line through it, subtract 3 (the number derived from Step 13) from it. Enter the result in the same position in Matrix 4.
Step 15: To each number in Matrix 3 that is at the intersection of two lines, add 3 (the number derived from Step 13). Enter the result in the same position in Matrix 4.
This will give Matrix 4.
Matrix 4
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
1 |
(0 + 3) 3 |
2 |
0 |
J2 |
(3 – 3) 0 |
0 |
2 |
1 |
J3 |
(5 – 3) 2 |
0 |
0 |
3 |
J4 |
3 |
(1 + 3) 4 |
0 |
2 |
Now we need to apply the test from Step 3 to Matrix 4: no row or column (in the pattern) contains more than one zero.
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
1 |
3 |
2 |
0 |
J2 |
0 |
0 |
2 |
1 |
J3 |
2 |
0 |
0 |
3 |
J4 |
3 |
4 |
0 |
2 |
Step 16: Go back to Matrix 1. The squared numbers in Matrix 4 show which ones to pull out of Matrix 1. Put these numbers into a new Matrix 5 by themselves. This new Matrix 5 indicates that one optimal solution for the problem is to assign job 1 to man 4; job 2 to man 2; job 3 to man 2 and job 4 to man 3. The number in Matrix 5 shows the cost per unit for each assignment indicated. The sum of these numbers (£17) is the minimum total cost. This sum will be the same for any of the optimal solutions, if there is more than one – i.e. 9 + 5 + 1 + 2 = £17 per hour.
Matrix 5
Men/jobs |
M1 |
M2 |
M3 |
M4 |
J1 |
– |
– |
– |
9 |
J2 |
5 |
– |
– |
– |
J3 |
– |
1 |
– |
– |
J4 |
– |
– |
2 |
– |
 SUMMARY
SUMMARY
This chapter has introduced you to a range of processes for analysing manufacturing operations. Care must be taken to ensure that data are valid and that the right technique is used. Some of these techniques can also be used in service operations. However, there are additional techniques that are better suited to service operations, and these are provided in the following chapter.
 Key terms
Key terms
Assignment modelling
Bi-variate formula
Correlation analysis
Index numbers
Linear functions
Regression
Time series analysis