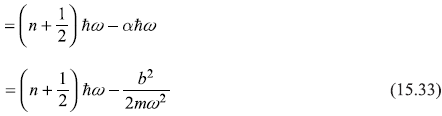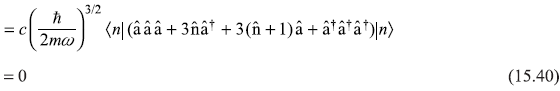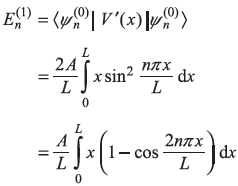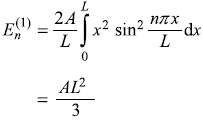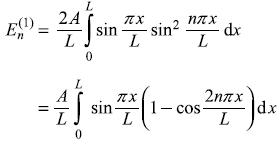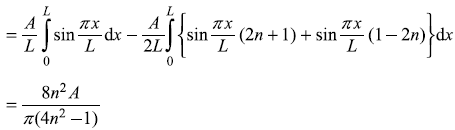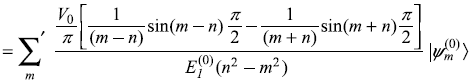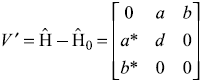Chapter 15
Time-independent Perturbation Theory
15.1 INTRODUCTION
We have seen in the first part of the book that it is possible to solve Schrodinger equation exactly (i.e., the energy eigenvalues and eigenfunctions may be found exactly) for a particle in potential like harmonic potential or Coulomb potential. However, many a times, there are situations in which the potential is deviating a bit from the potentials for which Schrodinger equation may be solved exactly. For example, if a particle is put in a potential, deviating from harmonic potential, that is, if potential is ![]() it is not possible to find exact eigenvalues and eigenfunctions of this so-called anharmonic potential. But it is possible to find approximate solutions of the Schrodinger equation when (in the above example) the potential is deviating from the harmonic potential by only small amount, that is, when constants a and b (appearing in the above mentioned potential) are very small. In this chapter, we shall develop time-independent perturbation theory which shall give approximate eigenvalues and eigenstates of the system that have potential differing by small amount from the standard potential for which Schrodinger equation may be solved exactly.
it is not possible to find exact eigenvalues and eigenfunctions of this so-called anharmonic potential. But it is possible to find approximate solutions of the Schrodinger equation when (in the above example) the potential is deviating from the harmonic potential by only small amount, that is, when constants a and b (appearing in the above mentioned potential) are very small. In this chapter, we shall develop time-independent perturbation theory which shall give approximate eigenvalues and eigenstates of the system that have potential differing by small amount from the standard potential for which Schrodinger equation may be solved exactly.
15.2 NON-DEGENERATE PERTURBATION THEORY
The perturbation theory, which we are going to discuss in this Chapter, is applicable when following criteria are satisfied:
- The total Hamiltonian of the system may be written as the sum of two parts.
Ĥ = Ĥ0 + Ĥ′ (15.1)
- The eigenvalues and eigenstates of the so-called unperturbed Hamiltonian Ĥ0 are known, and
- The second part of the total Hamiltonian, Ĥ′ (Ĥ′ is known as perturbation) is much smaller, in comparison to the unperturbed Hamiltonian Ĥ0 (as we proceed, the criterion that decides the smallness of Ĥ′ will become clear).
The last criterion is equivalent to the underlying assumption:
- The eigenvalues and eigenstates of the total Hamiltonian Ĥ do not differ appreciably from those of the unperturbed Hamiltonian Ĥ0.
We start with the Schrodinger equation for the unperturbed Hamiltonian
where eigenvalues ![]() and eigenstates
and eigenstates ![]() are known. For example, Ĥ0 may represent the Hamiltonian of a particle in a one-dimensional harmonic potential, for which (as seen in Chapter 6) we know eigenvalues
are known. For example, Ĥ0 may represent the Hamiltonian of a particle in a one-dimensional harmonic potential, for which (as seen in Chapter 6) we know eigenvalues ![]() and eigenstates
and eigenstates ![]() . Here, our aim is to develop a method to solve the Schrodinger equation for the total Hamiltonian Ĥ, that is,
. Here, our aim is to develop a method to solve the Schrodinger equation for the total Hamiltonian Ĥ, that is,
As mentioned earlier, it may not be possible to solve Eq. (15.3) exactly, therefore, our aim is to obtain approximate expressions for En and ψn.
Now, owing to smallness of Ĥ′, En, and ψn may not be differing much from ![]() and
and ![]() and, therefore, it is possible to write
and, therefore, it is possible to write
where ∆ψn and ∆En are small corrections to ![]() and
and ![]() , respectively. Perturbation theory is all about to find these small corrections for given small perturbation potential Ĥ′. In what follows, we rewrite Ĥ′ as λĤ′, where λ is a dummy variable and may be given any small value between 0 and 1. The time-independent Schrodinger equation, whose solution we seek, then, is
, respectively. Perturbation theory is all about to find these small corrections for given small perturbation potential Ĥ′. In what follows, we rewrite Ĥ′ as λĤ′, where λ is a dummy variable and may be given any small value between 0 and 1. The time-independent Schrodinger equation, whose solution we seek, then, is
Since ![]() as λ → 0, it is consistent to express ψn(Εn) in the form of a series in powers of λ with its leading term as
as λ → 0, it is consistent to express ψn(Εn) in the form of a series in powers of λ with its leading term as ![]()
Here the superscripts 0, 1, 2, ... refer to the order of the perturbation. The parameter λ may take a continuous range of values between 0 and 1, and we shall set λ = 1 in the final result. Substituting the expansion of ψn and En [Eqs (15.6) in Eq. (15.5)], we get

Since this equation is to be true for all values of λ (in the interval [0, 1]), the coefficients of equal powers of λ on both sides of this equation have to be equal. Equating the terms independent of λ, we have
Next, equating the coefficients οf λ give
while coefficients of λ2 give
and so on.
15.2.1 The First-order Correction
We know that the eigenstates ![]() of unperturbed Hamiltonian Ĥ0 form a complete (orthonormal) set. Therefore, each term in Eq. (15.6a) may be expressed as a linear combination of the functions
of unperturbed Hamiltonian Ĥ0 form a complete (orthonormal) set. Therefore, each term in Eq. (15.6a) may be expressed as a linear combination of the functions ![]() . For considering first-order correction, let us express
. For considering first-order correction, let us express ![]() in terms of
in terms of ![]() as
as
Here ![]() are the expansion coefficients to be determined. Substituting the expansion (15.8) in Eq. (15.7b), we get
are the expansion coefficients to be determined. Substituting the expansion (15.8) in Eq. (15.7b), we get
or
Here we have used Eq. (15.2) in writing the first term on L.H.S. of Eq. (15.9). Let us multiply the above equation from left by ![]() and integrate over the entire allowed space, we get
and integrate over the entire allowed space, we get
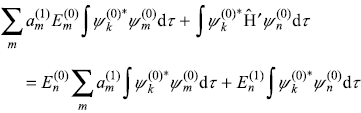
or
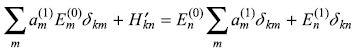
or
or
where orthonormality of the set {![]() }
dictates
}
dictates
and ![]() is the matrix element given as
is the matrix element given as
For k ≠ n, Eq. (15.10) gives
and for k = n
![]() is the first-order correction to eigenvalue En under the perturbation Ĥ′. Putting value of coefficient
is the first-order correction to eigenvalue En under the perturbation Ĥ′. Putting value of coefficient ![]() from Eq. (15.12a) in Eq. (15.8), we get value of
from Eq. (15.12a) in Eq. (15.8), we get value of ![]() , the first-order correction to eigenstate ψn,
, the first-order correction to eigenstate ψn,

Therefore, we may conclude that the eigenvalue and eigenstate to first order are:
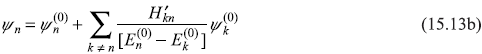
15.2.2 The Second-order Correction
The second-order correction to the eigenstate, ![]() , may be expanded as a linear combination of the complete set of orthonormal eigenstates of Hamiltonian Ĥ0, as
, may be expanded as a linear combination of the complete set of orthonormal eigenstates of Hamiltonian Ĥ0, as

Substituting Eqs (15.14) and (15.8) in Eq. (15.7c), we have

Multiplying the above equation from left by ![]() and integrating, we get
and integrating, we get

or
15.2.2.1 Second-order Correction to Eigenvalues
For k = n, we have from Eq. (15.15)
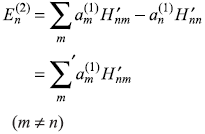
or

Last expression has been obtained by using expression for ![]() from Eq. (15.12a). Here we have used the relation
from Eq. (15.12a). Here we have used the relation ![]()
15.2.2.2 Second-order Coefficients
For k ≠ n, we get from Eq. (15.15)
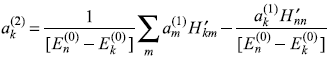
Putting the value of ![]() from Eq. (15.12a), it gives
from Eq. (15.12a), it gives
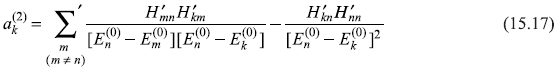
15.3 HARMONIC OSCILLATOR SUBJECT TO PERTURBING POTENTIAL
Before proceeding further to discuss perturbation theory applicable to degenerate states, let us apply the results of non-degenerate perturbation theory to a simple case of one-dimensional harmonic oscillator subject to a small perturbing potential. Let us consider a one-dimensional harmonic oscillator described by the Hamiltonian.
which is perturbed by a small anharmonic potential
We shall consider various forms of the perturbing potential [e.g., g(x) = bx and g(x) = bx2]. We have to find the first and second-order corrections to the unperturbed energy eigenvalues of Hamiltonian Ĥ0; the unperturbed eigenvalues and eigenstates are given by the Schrodinger equation

In Chapter 6, the equation was solved and the results for ![]() and
and ![]() were obtained as
were obtained as
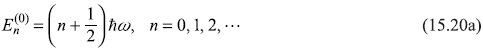
where
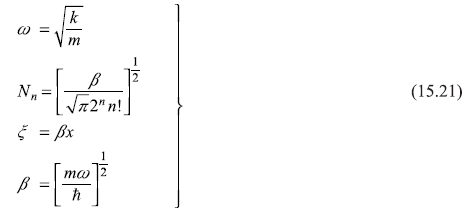
In the language of the creation and annihilation operators a† and a, and bra and ket notations of eigenstates, the Eqs (15.18a) and (15.19) may be written as (see Chapter 8)

with
15.3.1 Perturbing Potential Varying as x
As a simple case, firstly, we consider the perturbing potential
The first-order correction to the unperturbed eigenvalue ![]() of state
of state ![]() is
is
Putting value of x from Eq. (15.25), we get
Using the rules of operation of â and ↠on eigenket ![]() viz.
viz.
we can easily check that
The second-order correction to En is
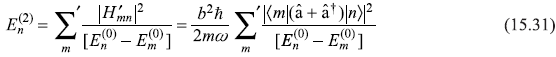
or
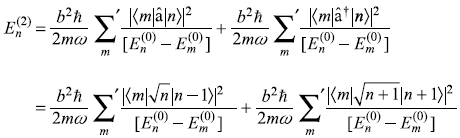
Noting that the matrix elements
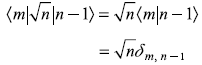
and

we get
or
The dimensions of constant b (in the perturbing potential bx) are such that the quantity (b2/2mω3ħ) is dimensionless. Let this small dimensionless quantity be denoted by α. So,
As a result, the new energy levels of the perturbed oscillator are
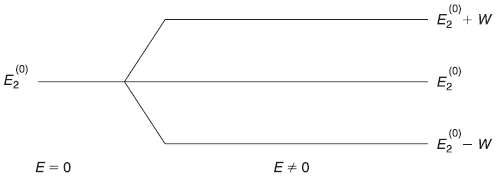
The new energy levels are simply the old energy levels, each shifted downwards by (same amount) (b2/2mω2), as shown in Figure 15.1.
In fact, the Schrodinger equation corresponding to the Hamiltonian
may be solved exactly. We may re-write Eq. (15.34) as
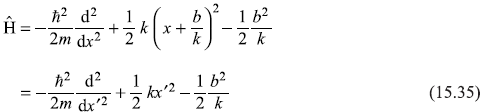
with the change of coordinate x′ = x + (b/k)
Now, Eq. (15.35) is representing the Hamiltonian of a harmonic oscillator with same force constant k and same frequency ω as that with Ĥ0 but with shifted origin of coordinate and of energy. Therefore, the solution of Schrodinger equation corresponding to the Hamiltonian equation (15.35) gives exact result:
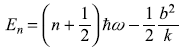
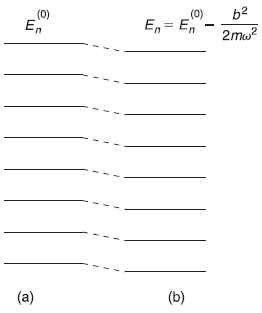
Figure 15.1 Energy levels of a one-dimensional harmonic oscillator (a) Unperturbed (b) Perturbed by the potential V′(x) = bx (up to second order)
Comparing Eqs (15.33) and (15.36) we observe that our second-order perturbation correction, in fact, gives exact results of energy levels of harmonic oscillator perturbed with linear potential.
The fact that perturbation theory gives same result as obtained by exact solution of the Schrodinger equation for linearly perturbed harmonic oscillator, clearly validates the perturbation theory. Let us mention here that it is generally not possible to solve Schrodinger equation for perturbed system, exactly, as mentioned in Section 15.1. For example, if the perturbation potential is Ĥ′ = cx3, it is not possible to solve the corresponding Schrodinger equation exactly. We study this case in the following sub-section.
15.3.2 Perturbing Potential Varying as x3
Let us next consider the one-dimensional harmonic oscillator subject to a small perturbing potential
Using Eq. (15.25), we may write x3 term as
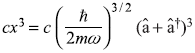
Making use of the operator relations
(â + â†)3 may be written as
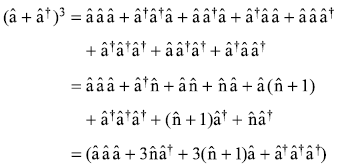
So the perturbation term is
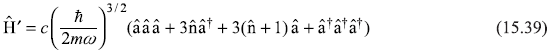
The first-order correction
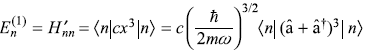
The four terms of second-order correction ![]() may be written as
may be written as
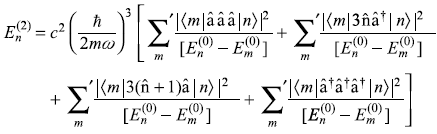
First term
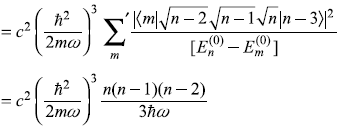
Second term
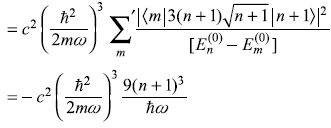
Third term

Fourth term
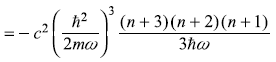
So


where dimensionless quantity A is

Figure 15.2 Energy levels of a one-dimensional harmonic oscillator (a) Unperturbed (b) Perturbed by the potential V′(x) = cx3 (up to second order)
In Figure 15.2, we show, schematically, the unperturbed as well as the perturbed energy levels. We observe that the effect of Ĥ′ is to lower all the unperturbed energy levels, whatever be the sign of constant c appearing in Ĥ′. Also we notice that larger the n, larger is the amount by which ![]() is lowered by perturbation.
is lowered by perturbation.
15.4 DEGENERATE PERTURBATION THEORY
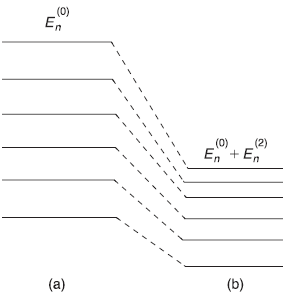
Many a times, we encounter a situation where the unperturbed states are degenerate. In fact, if the potential in which a particle moves, contains symmetry, many of the resulting eigenstates are degenerate. For example, in hydrogen atom, where the electron moves in a spherically symmetric potential, we get, for instance, three-fold degenerate p-states, five-fold degenerate d-states, and so on. In case of q-fold degenerate states, q different eigenstates of the system have same energy eigenvalue. However, if the symmetry of the potential producing q-fold degeneracy is destroyed by applying a small perturbation Ĥ′, the degeneracy is (partly or fully) removed, that is, the different eigenstates that have same energy eigenvalues in absence of perturbation may now have different energies, [shown schematically in Figure (15.3)].
The perturbation theory developed in Section 15.2 shall not be applicable to the case of degenerate states. For example, Eqs (15.12c) and (15.16) may diverge in case of degenerate states. Therefore, there is no reason to trust even the first-order correction to energy [Eq. (15.12b)] for the degenerate case. We have to look for an alternative method to deal with degenerate states. In this section, we describe the perturbation method for degenerate states.
15.4.1 Two-fold Degeneracy
Let us consider a system, which when unperturbed has two of its eigenstates ![]() and
and ![]() with same energy eigenvalue E(0),
with same energy eigenvalue E(0),
Figure 15.3 Lifting the two-fold degeneracy by a perturbation
and
With ![]() and
and ![]() both normalized. It may be easily seen that any linear combination of those states
both normalized. It may be easily seen that any linear combination of those states
where c1 and c2 are arbitrary constants, is also an eigenstate of Ĥ0, with same eigenvalue E(0), that is,
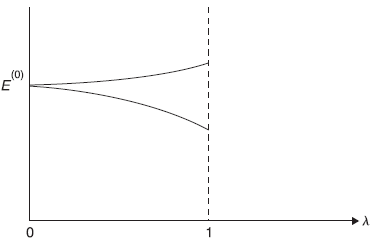
Generally, the perturbation λ Ĥ′ lifts the two-fold degeneracy. As shown schematically in Figure 15.3, the unperturbed energy E(0) splits into two values as λ increases from 0 to 1. It is not clear, to begin with, which initial unperturbed state should be taken (i.e., what values of constants c1 and c2 should be taken) for implementation of the perturbation. So we start with arbitrary (but adjustable) constants c1 and c2 in ψ(0)). We want to solve the Schrodinger equation
with
Putting these expansions of E and ψ in Eq. (15.46) and collecting coefficients of equal powers οf λ, we get
Equating the terms independent of λ, we have
Next, equating the coefficients of λ gives
Putting the expansion (15.44) of ψ(0) in the above equation gives
Multiplying above equation from left by ![]() and integrating over the allowed space, we get
and integrating over the allowed space, we get
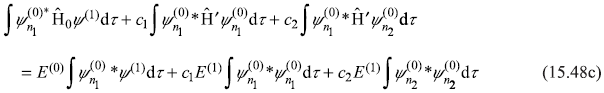
As Ĥ0 is Hermitian operator, the Hermitian conjugate of Eq. (15.43a) gives
which gives
that is, the first term on L.H.S. of Eq. (15.48c) cancels the first term on its R.H.S. Then Eq. (15.48c) results in
where
and where we have used the orthogonality condition (15.43c).
Again, multiplying Eq. (15.48b) from left by ![]() and integrating, we get
and integrating, we get
Equations (15.49a) and (15.49c) may be put in matrix form as
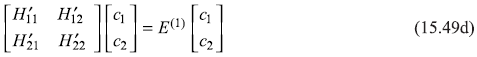
which has a non-trivial solution if the characteristic determinant vanishes, giving the secular equation

From this, we get
or
It may be noted here that the quantities ![]() appearing in Eq. (15.51) for the expression of
appearing in Eq. (15.51) for the expression of ![]() are in principle known as these are just “matrix elements” of Ĥ′ (the given perturbation potential) with respect to the known unperturbed eigenstates
are in principle known as these are just “matrix elements” of Ĥ′ (the given perturbation potential) with respect to the known unperturbed eigenstates ![]() and
and ![]() . So, on perturbation, the unperturbed energy E(0) changes to
. So, on perturbation, the unperturbed energy E(0) changes to
thereby lifting the two-fold degeneracy (if ![]() and
and ![]() are different).
are different).
Let us, next, proceed to find the coefficients c1 and c2. We start with the two equations in c1 and c2 [Eqs (15.49a) and (15.49c)].
along with the normalization condition [on ψ(0) Eq. (15.44)]
It is straightforward to find values of c1 and c2 from above three equations as
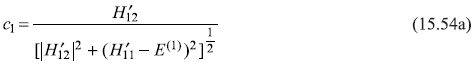

It may be noted here that as E(1) has two different values ![]() and
and ![]() (giving rise to different values
(giving rise to different values ![]() to energy), the coefficients c1 and c2 shall also have two different set of values:
to energy), the coefficients c1 and c2 shall also have two different set of values: ![]() and
and ![]() (for value
(for value ![]() ) and
) and ![]() and
and ![]() (for value
(for value ![]() ). Therefore, the wave function
). Therefore, the wave function
corresponds to the perturbed energy ![]() and the wave function
and the wave function
for perturbed energy ![]() .
.
15.4.2 g-Fold Degeneracy
The method of previous section may be easily generalized to the case when an energy level is g-fold degenerate. As we saw in the case of two-fold degeneracy, E(1)’S are nothing but the eigenvalues of the 2 × 2 H′ -matrix [Eq. (15.49d)]. Equation (15.50) is the corresponding characteristic equation for this matrix and, in fact, the linear combination of the unperturbed states are the eigenvectors of Ĥ′. So, in case of g-fold degeneracy, we should look for the eigenvalue equation
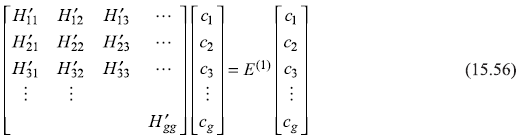
which, for nontrivial solutions, give the secular equation.
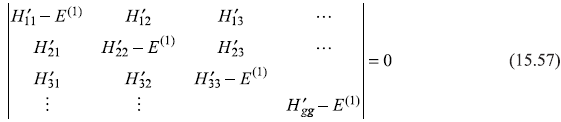
15.5 THE STARK EFFECT
As an example of the application of degenerate perturbation theory, let us consider how a uniform time-independent electric field affects the energy levels of hydrogen atom. The corresponding change in frequency of the associated spectral lines, as a result of the applied uniform electric field is called the stark effect.
Let us consider a hydrogenic atom with nuclear charge Ze in a uniform time-independent electric field E = E ez, pointing in z-direction. The potential energy of the electron of charge –e in this field is
The total Hamiltonian of the one-electron atom in this electric field is
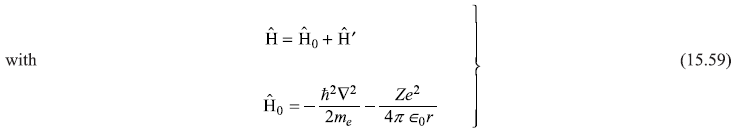
We know from Chapter 10 that the energy eigenvalue equation of the unperturbed atom
or
gives eigenstates ![]() which are n2-fold degenerate. We shall see in this section how the perturbing uniform electric field E removes (partly) this degeneracy. Let us, specifically, consider the four-fold degenerate n = 2 states, all with same unperturbed eigenvalue (see Section 10.8.1).
which are n2-fold degenerate. We shall see in this section how the perturbing uniform electric field E removes (partly) this degeneracy. Let us, specifically, consider the four-fold degenerate n = 2 states, all with same unperturbed eigenvalue (see Section 10.8.1).
The four eigenstates corresponding to n = 2 are given as (see Section 10.8)
- n = 2, l = 0, m = 0
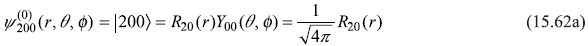
- n = 2, l = 1, m = 1
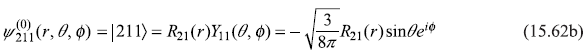
- n = 2, l = 1, m = 0
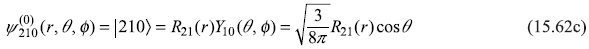
- n = 2, l = 1, m = – 1

where
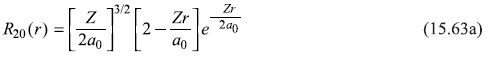
and
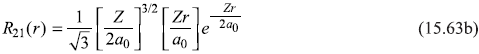
Let us use following shorthand notations for the four states:
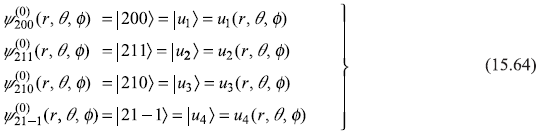
To calculate the change in energy ![]() , we must solve the corresponding secular equation [see Eq. (15.57)].
, we must solve the corresponding secular equation [see Eq. (15.57)].
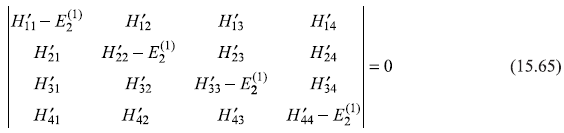
Now we have two observations: (1) For a system with symmetric potential, that is, for a potential with property V(r) = V (–r), the eigensates are either symmetric or anti-symmetric in position co-ordinates. In other words, the eigenstates have definite parity: even parity or odd parity. The electron in hydrogenic atom has spherically symmetric potential and, therefore, its eigenstates are with even or odd parity. The eigenstates are, in fact, even for the azimuthal quantum number l even and odd for l odd. So eigenstate ![]() has even parity and states
has even parity and states ![]() have odd parity. (2) The perturbation Ĥ′ = |e|Ez = |e| Ercosθ is an odd function (under space inversion).
have odd parity. (2) The perturbation Ĥ′ = |e|Ez = |e| Ercosθ is an odd function (under space inversion).
On these counts, the matrix element ![]() is non-zero if
is non-zero if ![]() and
and ![]() have opposite parity; only for these cases, the integrand of the corresponding integral,
have opposite parity; only for these cases, the integrand of the corresponding integral,
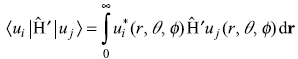
is an even function. The matrix elements ![]()
So secular equation (15.65) gives
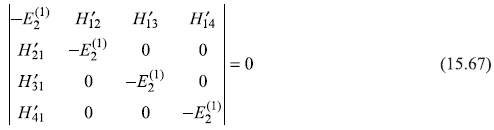
Now we know that z commutes with ![]() and, therefore,
and, therefore, ![]() commutes with
commutes with ![]() , that is,
, that is,
Taking matrix elements of both sides of Eq.(15.68) in between states ![]() and
and ![]() we have
we have
or,
or
So
For n1 = 2, l1 = 0, n2 = 2, l2 = 1, we have
and Eq. (15.67) gives
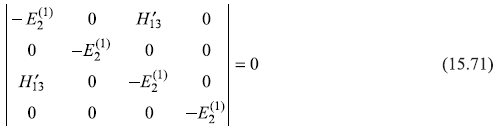
So the only non-vanishing matrix element is
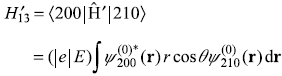
Putting values from Eqs (15.62) and (15.63), we get (for hydrogen atom Z = 1)
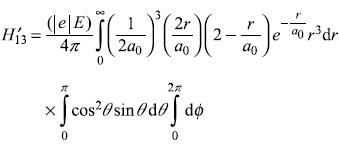
Putting these values in Eq. (15.71) gives
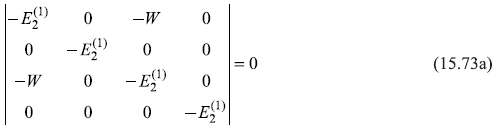
which gives four values of ![]()
Thus to first order, the four-fold degenerate n = 2 states of hydrogen atom split into three different energies, as shown schematically in Figure 15.4.
Let us now proceed to find out the new (i.e., the perturbed) eigenstates with corresponding energy eigenvalues ![]() and
and ![]() . We express the perturbed eigenstates ψ(0) in terms of
. We express the perturbed eigenstates ψ(0) in terms of
the four (unperturbed) states ![]() and
and ![]() as
as
Figure 15.4 Splitting of n = 2 levels of hydrogen atom in the presence of a homogeneous electric field E
where coefficients c1, c2, c3, c4 are determined by the matrix equation [see general matrix equation (15.56)].
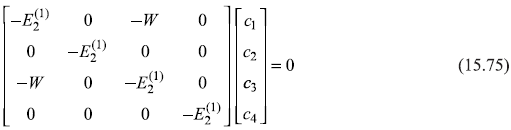
which gives four equations
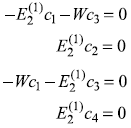
For ![]() we get c1 = –c3, c2 = c4 = 0 and Eq. (15.74) gives the required eigenstate as
we get c1 = –c3, c2 = c4 = 0 and Eq. (15.74) gives the required eigenstate as
Similarly for ![]() , we get c1 = c3, c2 = c4 = 0 and the corresponding eigenstate is
, we get c1 = c3, c2 = c4 = 0 and the corresponding eigenstate is
However, for the case of ![]() , we get c1 = c3 = 0 and c2 and c4 are arbitrary. So we may write,
, we get c1 = c3 = 0 and c2 and c4 are arbitrary. So we may write,
with ![]()
We notice here that the perturbing electric field mixes the m = 0 states ![]() and
and ![]() forming two different states
forming two different states ![]() and
and ![]() with perturbed energies
with perturbed energies ![]() and
and ![]() respectively. On the other hand, the m = 1, –1 states
respectively. On the other hand, the m = 1, –1 states ![]() and
and ![]() are left degenerate with unchanged energy
are left degenerate with unchanged energy ![]() .
.
15.6 THE FINE STRUCTURE OF HYDROGEN
While finding energy eigenvalues and eigenstates of hydrogen atom, we considered the Hamiltonian,
where me represents the reduced mass of electron. In fact, by replacing the electron mass by the reduced mass in Eq. (15.77), we have already taken into account the correction because of the motion of proton (nucleus) around the centre of mass of proton and electron. There are still more factors which, really, affect the eigenvalues and eigenstates of the electron in hydrogen atom. We mention here, in brief, these effects starting with the most significant.
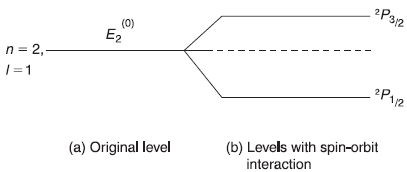
- Most significant of these effects is the so-called fine structure. In fact, the fine structure arise due to two different mechanisms: (a) due to relativistic correction (variation of electron mass with the velocity) and (b) due to spin–orbit interactions. Both of these effects produce changes in the energy levels which are relatively small. The relative changes are of the order of α2, where α[= (e2/4π∊0hc) ≈ (1/137)] is the famous fine structure constant. In this section, we will study only the effect of spin-orbit interactions towards fine structure.
- In the quantum mechanical treatment of electromagnetic field, there are zero-point energy states [just like the residual energy of a quantum harmonic oscillator, which is called its zero-point energy (Chapter 6)]. The ever-present so-called vacuum fluctuations of electrodynamic field produce a small change in energy levels of electrons in atom. This is called the Lamb shift and is relatively of order α3.
- The magnetic interaction between the spin magnetic moment of electron and that of proton, produces changes in the energy levels, which are of the order of (me/mp)α4, and give rise to what is known as the hyperfine structure.
In this section, we shall consider the fine structure due to spin–orbit interactions. In order to understand the spin–orbit interaction, we consider a simple classical model of the electron orbiting around the nucleus. Let us imagine an observer at rest with the orbiting electron. From the observer’s point of view, the nucleus is circling around him (and the electron) [see Figure (15.5)].
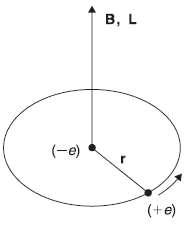
Figure 15.5 Hydrogen atom seen in electron’s frame of reference
The circulating positive charge, which constitutes a current in the orbit, sets up a magnetic field B at the electron
with effective current I = e/T (e is proton charge and T is period of the orbit). Now, in the rest frame of the proton, the orbital angular momentum of the electron is given as
From Eqs (15.78) and (15.79), we have
as B and L point in the same direction. Now, we already know that the magnetic moment vector μ associated with the electron spin angular momentum vector S is given as
Therefore, the electron with its spin magnetic moment μs is present there in the magnetic field B due to proton. The interaction energy of μs in field B is
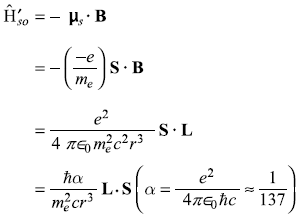
Actually this is not correct. In fact, the rest frame of electron is not an inertial frame (but an accelerating frame) as the electron is orbiting around the nucleus. This fact produces the so-called Thomas precession effect and reduces the interaction energy by a factor of 2. Thus the correct interaction is
This spin–orbit interaction is due to the torque exerted on the spin magnetic moment μs of the electron by the magnetic field B of the proton in the electron’s instantaneous rest frame.
As we had seen in Section 13.2, the orbital angular momentum operator ![]() and the spin angular momentum operator Ŝ do not commute with the total Hamiltonian
and the spin angular momentum operator Ŝ do not commute with the total Hamiltonian ![]() . However, the total angular momentum operator
. However, the total angular momentum operator ![]() and
and ![]() commute with Ĥ. Therefore, these quantities are conserved. In other words, the eigenstates of
commute with Ĥ. Therefore, these quantities are conserved. In other words, the eigenstates of ![]() and
and ![]() are simultaneous eigenstates of total Hamiltonian Ĥand may be used in the perturbation theory.
are simultaneous eigenstates of total Hamiltonian Ĥand may be used in the perturbation theory.
As the Hamiltonian ![]() contains spin–orbit interaction, the wave function of the electron should contain both the space as well as spin part. So it will be most appropriate to write electron states in terms of Pauli wave functions.
contains spin–orbit interaction, the wave function of the electron should contain both the space as well as spin part. So it will be most appropriate to write electron states in terms of Pauli wave functions.
The Pauli wave functions of the unperturbed Hamiltonian Ĥ0, written in Pauli operator form as

are

Pauli wave equation for the unperturbed Hamiltonian (Ĥ0)P is given by
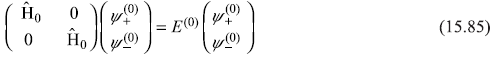
Or
and
The energy E(0) simply represents the energy levels of unperturbed hydrogen atom
The wave functions ![]() are simply Pauli wave functions of electron with up and down spin states.
are simply Pauli wave functions of electron with up and down spin states.


In the absence of spin–orbit interactions, both the above states have same energy. Therefore, any linear combination of these states is an eigenstate with same energy. We would like to form two mutually orthogonal states as linear combinations of these two states, in which the Hamiltonian ![]() is diagonal. Then all the operators
is diagonal. Then all the operators ![]() represented in these new states, will be diagonal. Such new states may be formed by going from the uncoupled representation (where
represented in these new states, will be diagonal. Such new states may be formed by going from the uncoupled representation (where ![]() are well defined) to the coupled representation (where
are well defined) to the coupled representation (where ![]() are well defined), that is, using the Clebsch–Gordon coefficients (discussed in Chapter 13). With the help of C–G coefficients given in Table 13.1, we may easily write Pauli wave functions in coupled representation (see Section 13.6):
are well defined), that is, using the Clebsch–Gordon coefficients (discussed in Chapter 13). With the help of C–G coefficients given in Table 13.1, we may easily write Pauli wave functions in coupled representation (see Section 13.6):
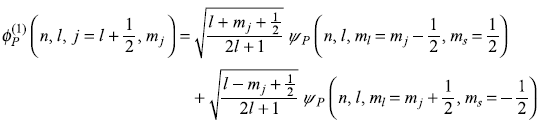
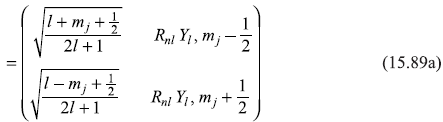
And a similar expression for the other Pauli wave function is
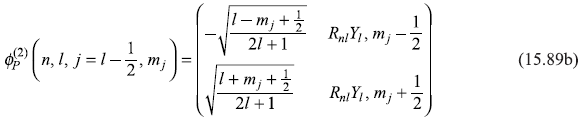
Now, as mentioned above, the states ![]() and
and ![]() are simultaneous eigenstates of operators
are simultaneous eigenstates of operators ![]() and
and ![]() i.e.
i.e.

and
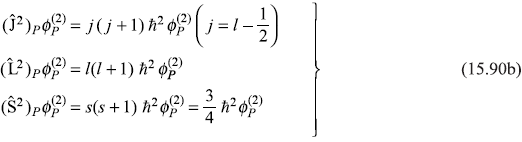
We have
so
Therefore, the first-order correction to energy due to spin–orbit interaction is given by
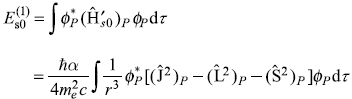
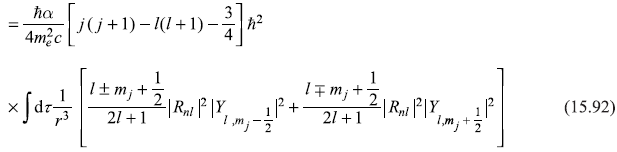
Here, one may note, the upper sign corresponds to the case j = [l + (1/2)] and the lower sign for j = [l – (l/2)].
The integration over angles may be easily carried out and we get,

or
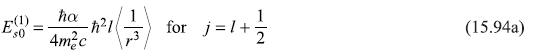
and

where

Therefore,
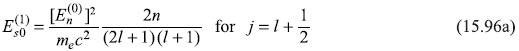
and
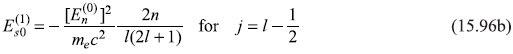
Figure 15.6 Fine structure due to spin–orbit interaction of 2P1/2 and 2P3/2 levels of hydrogen atom
For the particular case of l = 1, we get
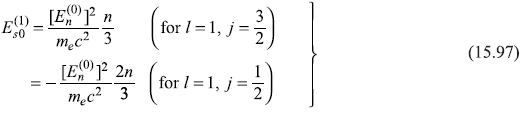
In Figure 15.6, we show schematically the splitting of a level due to spin–orbit interaction.
15.7 THE ZEEMAN EFFECT
It was firstly observed by Zeeman that when atoms radiate in presence of a magnetic field, their individual spectral lines split into many lines. The phenomenon came to be known as Zeeman effect. As we shall see the phenomenon is a clear confirmation of vector atom model and space quantization. Firstly we shall discuss the so-called Normal Zeeman effect, where a single spectral line splits into three lines in presence of a magnetic field. In the next section, we shall discuss the anomalous Zeeman effect, where a single spectral line splits into more than three lines.
15.7.1 Normal Zeeman Effect
We shall study the changes in energy levels of a hydrogen-like atom when it is put in a constant homogeneous magnetic field. Let the magnetic field be in z-direction.
In the normal Zeeman effect, we ignore the effect of spin magnetic moment and consider only the interaction of orbital magnetic moment with the magnetic field. Obviously, the results obtained should be applicable to the cases where total spin of the atom is zero. In the next section, we shall include the interaction of spin magnetic moment (also) with the magnetic field.
Let the orbital magnetic moment of the atom be μ1. The total Hamiltonian of the atom in presence of field B is given as
where
Ĥ may be re-written as
The Hamiltonian Ĥ0 has eigenvalue equation
Now as ![]() commutes with Ĥ0 (Chapter 10), so
commutes with Ĥ0 (Chapter 10), so ![]() and Ĥ0 have simultaneous eigenstates. Therefore, Schrodinger equation in presence of magnetic field B is
and Ĥ0 have simultaneous eigenstates. Therefore, Schrodinger equation in presence of magnetic field B is

which gives
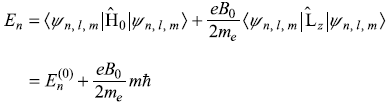
The (2l + 1) fold degenerate states ![]() which have energy
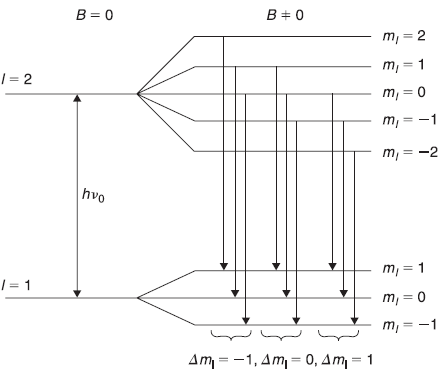
which have energy![]() in absence of B, have (2l + 1) (equi-spaced) different energies En in presence of B. The frequencies of the spectral lines emitted in transitions between two different states of the atom are given by
in absence of B, have (2l + 1) (equi-spaced) different energies En in presence of B. The frequencies of the spectral lines emitted in transitions between two different states of the atom are given by

or
where ∆m = m2 – m1 is the change of the magnetic quantum number m in the transitions. We know from selection rules (discussed in Chapter 17) that
and also that the light emitted in the transitions for which ∆m = 0, is polarized parallel to B while in transitions for which ∆m = ±1, the polarization is perpendicular to B. Thus, we get
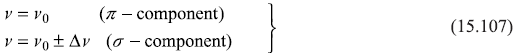
Figure 15.7 Normal Zeeman effect: Energy level corresponding to l = 2 splits into five and that corresponding to l = 1 splits into three levels. Because of the selection rule ∆ml = 1,0 –1, there are three spectral lines of energies (h v0 + µBB), h v0, and (h v0 – µBB)
where ∆v = (µBB0/h). We show in Figure 15.7 the schematic diagram of the possible transitions between levels with l2 = 2 and l1 = 1.
15.7.2 Anomalous Zeeman Effect
When a hydrogen-like atom is put in a constant homogeneous magnetic field and the atom has non-zero spin angular momentum, the Hamiltonian may be written as
Where

Here ![]() represents the spin-orbit interaction and Ĥ″ represents the interaction of atom with magnetic field B. We shall assume the field B to be weak such that the effect of interaction Ĥ″ is smaller than that of spin-orbit interaction. So, we shall consider the eigenstates of
represents the spin-orbit interaction and Ĥ″ represents the interaction of atom with magnetic field B. We shall assume the field B to be weak such that the effect of interaction Ĥ″ is smaller than that of spin-orbit interaction. So, we shall consider the eigenstates of ![]() as basis states and shall treat Ĥ″ as a small perturbation.
as basis states and shall treat Ĥ″ as a small perturbation.
In Section 15.6, we found the Pauli wave functions [given by Eqs (15.89a) and (15.89b)] corresponding to j = [l + (1/2)] and j = [l – (1/2)], respectively, which work as basis states in presence of spin-orbit interaction ![]() . We found there that as a result of
. We found there that as a result of ![]() ,
the energy levels
,
the energy levels ![]() split and each level is characterized by well-defined values of J2, L2, and S2. We shall use these basis states of Eqs (15.89a) and (15.89b) to find the contribution of perturbation Ĥ″.
split and each level is characterized by well-defined values of J2, L2, and S2. We shall use these basis states of Eqs (15.89a) and (15.89b) to find the contribution of perturbation Ĥ″.
We may write the Pauli operator for Ĥ″ as

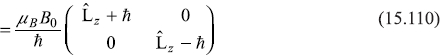
Now, as we know
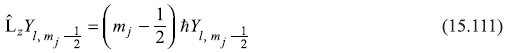
we may operate (Ĥ″)P on basis state ![]() [given by Eq. (15.89a)] to get
[given by Eq. (15.89a)] to get
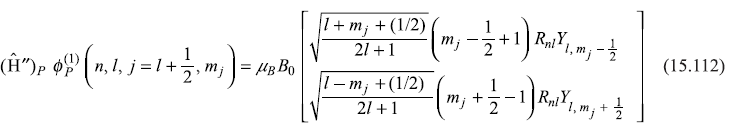
and
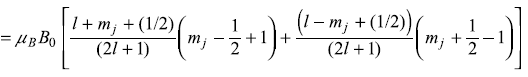

and similarly we get

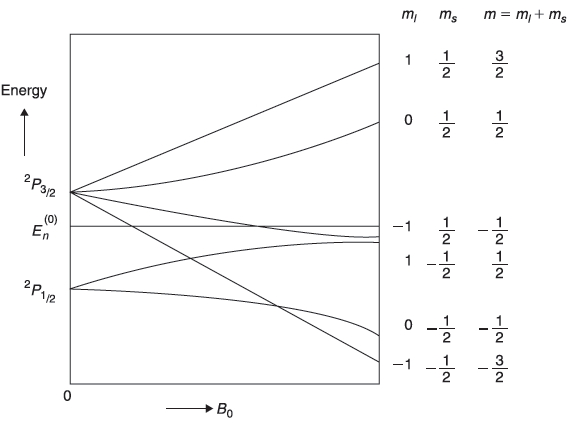
Figure 15.8 Schematic plot of the splitting of 2P energy level by magnetic field. The two levels corresponding to B0 = 0 represent the spin-orbit splitting
Let us consider the splitting of P-state (l = 1) of, say, an alkali atom. For l = 1, we have j = (3/2) and (1/2). So, we get
In Figure 15.8, we show schematically the splitting of 2P energy level by magnetic field.
EXERCISES
Exercise 15.1
Consider a particle in a one-dimensional potential box with walls at x = 0 and x = L. Find the first-order correction to ![]() and
and ![]() due to the following perturbations:
due to the following perturbations:
- V′(x) = Ax
- V′(x) = Ax2
-
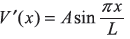
-
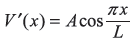
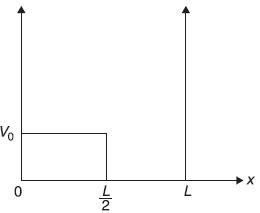
Figure 15.9 The potential raised by V0 in half the well
Exercise 15.2
A linear harmonic oscillator is perturbed by the potential
Find the first-order correction to energy ![]() .
.
Exercise 15.3
Consider a particle in a one-dimensional potential box with its walls at x = 0 and x = L, the system is perturbed such that the potential now is [see Figure (15.9)]
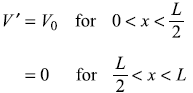
- Calculate the first-order correction to energy eigenvalues.
- Find the first-order correction to eigenstates.
- If the particle is an electron and it makes transitions, how do the frequencies emitted by the perturbed system compare with those of the unperturbed system?
- Up to what value of V0 are the perturbation theory results valid?
Exercise 15.4
A two-level unperturbed system is described by the Hamiltonian 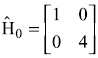 . Now a small perturbation is switched on, which may be represented by
. Now a small perturbation is switched on, which may be represented by 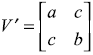
- Find the first-order correction to energy eigenvalues.
- Find the second-order correction to eigenvalues.
- Compare the eigenvalues including up to second-order corrections with the exact eigenvalues of Ĥ(= Ĥ0 + V′).
- Find eigenstates up to first-order correction.
The Hamiltonian of a three-level system is given as 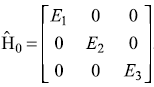 .
.
After a small perturbation, its Hamiltonian is given as 
- find the first-order corrections to energy eigenvalues.
- Find the second-order corrections to eigenvalues.
- Find out the first-order correction to eigenstates.
Exercise 15.6
A hydrogen atom in its ground state is put in a constant homogeneous electric field pointing in z-direction, so the interaction energy is H′ = eE0 r cosθ. Show that there is no change in the ground state energy of the atom up to first-order in the electric field.
Exercise 15.7
Consider a particle in a two-dimensional square potential well of side L.
Now a perturbation V′ is introduced such that
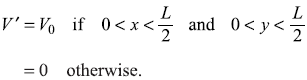
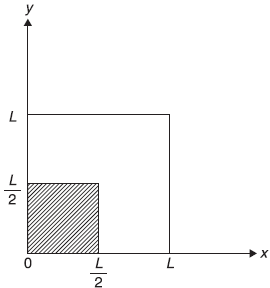
Figure 15.10 Two-dimensional potential well with (1/4)th part (shaded region) having potential raised by constant amount V0
This raises the potential in one quarter of the well by an amount V0 [see Figure (15.10)].
- Find the first-order correction to the ground state energy.
- Find the first-order correction to the first excited state energy.
Exercise 15.8
In Exercise 15.7, the particle in the two-dimensional square potential well, is perturbed by the potential V′ = V0 sin(πx/L). Find first-order correction to the energy of ![]() state.
state.
Exercise 15.9
When a hydrogen atom is put in a constant homogeneous electric field (in z-direction) the four-fold degeneracy of n = 2 states is partially lifted (the Stark effect). Estimate the electric dipole moment of hydrogen atom in the state.
Exercise 15.10
In Exercise 15.9, what is the electron charge density q(r, θ) associated with the state
Exercise 15.11
In a magnetic field of 2.0 T, the Zeeman components of a 550 nm spectral line are 0.028 nm apart. From these data find the ratio (e/me).
Exercise 15.12
An atomic gas it put in a magnetic field of 0.5 T. When suitably excited the atoms give spectral lines with Zeeman components. How far apart are the Zeeman components of the 590 nm spectral line?
SOLUTIONS
Solution 15.1
Solution 15.2
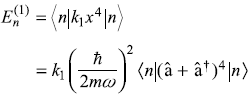
Only those terms contribute which have equal number of creation and annihilation operators. We get
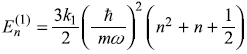
Solution 15.3
-
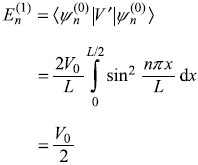
- The first-order correction to nth eigenstate is
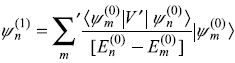
or

- As first-order correction to eigenvalue
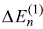 is same for all states, the emitted frequencies remain unchanged.
is same for all states, the emitted frequencies remain unchanged. - The results of perturbation theory are valid only for
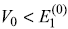 .
.
Solution 15.4
The unperturbed eigenvalues (of Ĥ0) are
![]() with corresponding eigenstate
with corresponding eigenstate 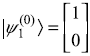
![]() with corresponding eigenstate
with corresponding eigenstate 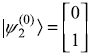
- First-order correction to eigenvalue
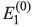
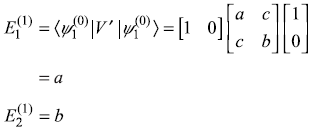
- Second-order corrections
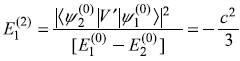
- So up to second-order, the energy levels are
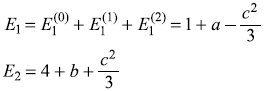
Exact eigenvalues of Ĥ are
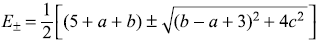
We may have binomial expansion for small values of c. Then

which give same values as E1 and E2 above, for small values of a and b.
- First-order corrections to eigenstates:
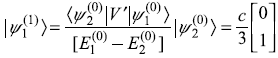
and, similarly

Therefore, normalized eigenstates including first-order correction are
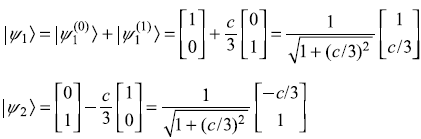
Solution 15.5
The unperturbed eigenvalues and eigenstates are
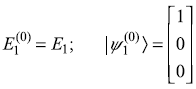
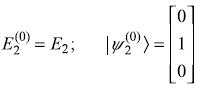

Perturbation Hamiltonian V′ is
- First-order correction to eigenvalues:
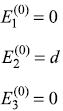
- Second-order corrections:

- First-order correction to eigenstates:
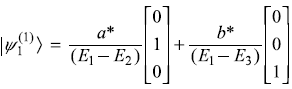
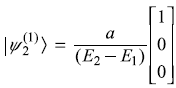
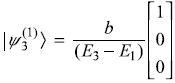
Solution 15.6
First-order correction to ground state energy of hydrogen atom
may be easily shown to vanish.
Solution 15.7
Unperturbed energy eigenvalues and eigenstates are
-

- The first excited states
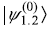 (let us call it
(let us call it  ) and
) and 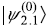 (call it
(call it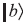 ) are doubly degenerate. Let us firstly construct the 2 × 2 matrix of the total Hamiltonian in these basis states.
) are doubly degenerate. Let us firstly construct the 2 × 2 matrix of the total Hamiltonian in these basis states.
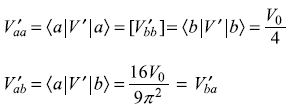
Therefore,
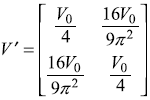
Using the results of doubly-degenerate perturbation theory, the changes in energy are given as Eq. (15.51)
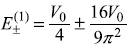
So the energy of first excited state, which was
 before perturbation, splits into two energies
before perturbation, splits into two energies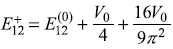
and

Solution 15.8
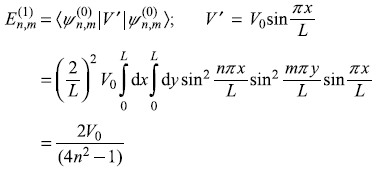
The interaction energy between an electric dipole moment D and the electric field E is [see Eq. (15.58)],
- We had found that eigenvalue of H′ in state
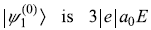
so
–D · E = 3|e|a0Eand
D = –3|e|a0ez(i.e., dipole moment is in opposite direction to electric field),
- In state
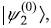 the eigenvalue of H′ is –3|e|α0Ε
the eigenvalue of H′ is –3|e|α0Ε
So
D = 3|e|a0ez(i.e., dipole moment is in the direction of electric field).
Solution 15.10
-

where
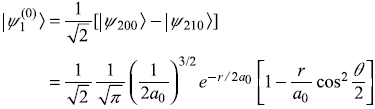
so
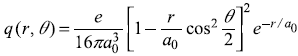
-
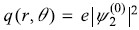
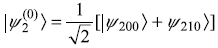
and
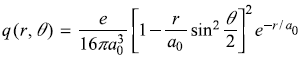
-
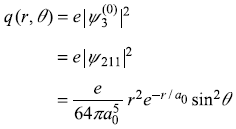
- same expression as above.
The separation of Zeeman components is
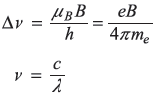
so
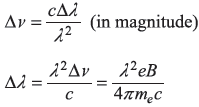
or
Solution 15.12
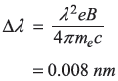
REFERENCES
- Levi, A.F.J. 2003. Applied Quantum Mechanics. Cambridge, MA.: Cambridge University Press.
- Matthews, P.T. 1974. Introduction to Quantum Mechanics, 3rd edn., London, UK: McGraw-Hill.
- Baym, G. 1969. Lectures on Quantum Mechanics. Massachusetts: Benjamin/Cummings.