The t-test is a basic tool in statistics used to compare the means of two samples. Its most strict version assumes that both samples are distributed according to a Gaussian distribution and have the same (unknown) variance.

In statistics, we refer to the null hypothesis as the hypothesis we want to test, and the alternative hypothesis as the one we use when the null is rejected. They are usually referred to as H₀ and H₁.

The t-test tests the equality of means from two populations, and it can be formulated in three possible ways:

• H₀: The means of the two populations are the same versus H₁: in that the means of the populations are different.
• H₀: The mean of population 1 is greater or equal than the one from population 2 versus H₁: the mean of population 1 is smaller than population 2.
• H₀: The mean of population 1 is smaller or equal than the one from population 2 versus H₁: the mean of population 1 is greater than population 2.

The user needs to define which one should be used, according to what needs to be tested. Each one will return a different p-value; in particular, the first one will be a two-sided test, and the other ones will be one-sided. What this means is that if we test (1), the p-value will be equivalent to the area to the right of the test statistic, plus the area to the left of the negative value of the test statistic (this is because the p-values reflect the probability that we get a test statistic as extreme or more extreme than the one we got, and since we are testing whether the means of both groups are equal, that difference could be positive or negative). 

The following screenshot shows the two sided test:

The following screenshot shows the left rejection area:

The following screenshot shows the right rejection  area:

The test statistic for this case is as follows:

S_p is the pooled standard deviation estimator (note that we are assuming that the variances are the same between the two groups):

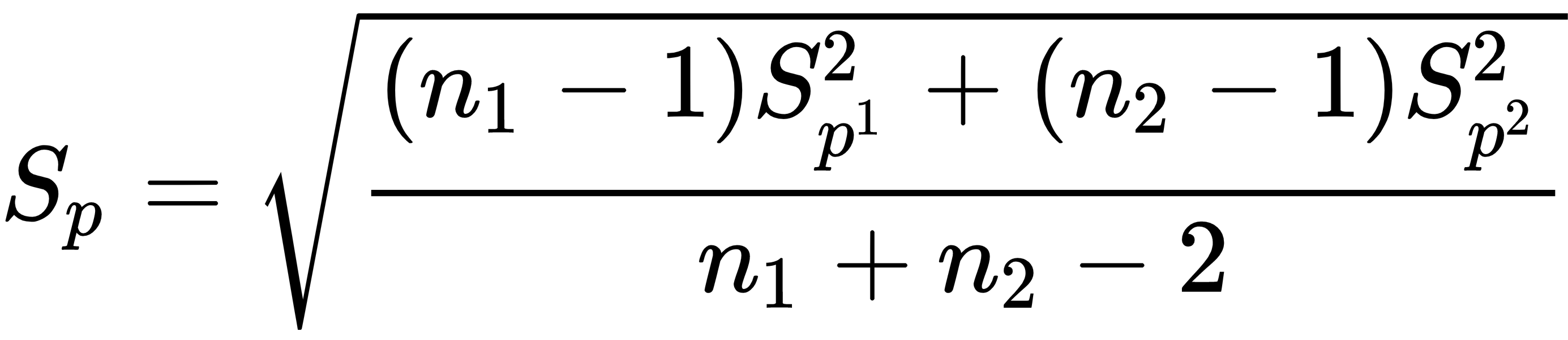
This is distributed according to a t-Student distribution with n₁+n₂-2 degrees of freedom. So far, we have assumed that both samples are distributed according to a Gaussian distribution, but sometimes that won't be the case. When the sample is small (<30), we really need the normality assumption. However, when the sample is large, it’s not strictly necessary. The reason is that.