
Floating-Point Representation on IBM Mainframes
Storage Format
SAS for z/OS uses the traditional IBM mainframe floating-point representation as
follows:
S E E E E E E E
Byte 1
M M M M M M M M
Byte 2
M M M M M M M M
Byte 3
M M M M M M M M
Byte 4
M M M M M M M M
Byte 5
M M M M M M M M
Byte 6
M M M M M M M M
Byte 7
M M M M M M M M
Byte 8
This representation corresponds to bytes of data with each character being 1 bit, as
follows:
• The S in byte 1 is the sign bit of the number. A value of 0 in the sign bit is used to
represent positive numbers.
• The seven E characters in byte 1 represent a binary integer known as the
characteristic. The characteristic represents a signed exponent and is obtained by
adding the bias to the actual exponent. The bias is an offset used to enable both
negative and positive exponents with the bias representing 0. If a bias is not used, an
additional sign bit for the exponent must be allocated. For example, if a system uses
a bias of 64, a characteristic with the value of 66 represents an exponent of +2,
whereas a characteristic of 61 represents an exponent of –3.
• The remaining M characters in bytes 2 through 8 represent the bits of the mantissa.
There is an implied radix point before the left-most bit of the mantissa. Therefore,
the mantissa is always less than 1. The term radix point is used instead of decimal
point because decimal point implies that you are working with decimal (base 10)
numbers, which might not be the case. The radix point can be thought of as the
generic form of decimal point.
Conversion Example
The following example shows the conversion process for the decimal value 512.1 to
hexadecimal floating-point representation. This example illustrates how values that can
be precisely represented in decimal cannot be precisely represented in hexadecimal
floating point.
1. Because the base is 16, you must first convert the value 512.1 to hexadecimal
notation.
2. First, convert the integer portion, 512, to hexadecimal using the base 16 number
system:
Base 16
16
7
...
16
4
16
3
16
2
16
1
16
0
268,435,456 ... 65,536 4096 256 16 1
70 Chapter 4 • SAS Variables

= ×200 .200 16
3
The value 512 is represented in hexadecimal as 200.
3. Write the hexadecimal number, 200, in floating-point representation. To do this,
move the decimal point all the way to the left, counting the number of positions that
you moved it. The number you moved it is the exponent:
= ×200 .200 16
3
4. Convert the fraction portion (.1) of the original number, 512.1 to hexadecimal:
.1 =
1
10
=
1.6
16
The numerator cannot be a fraction, so keep the 1 and convert the .6 portion again.
.6 =
6
10
=
9.6
16
Again, there cannot be fractions in the numerator, so keep the 9 and reconvert the .6
portion.
The .6 continues to repeat as 9.6 which means that you keep the 9 and reconvert. The
closest that .1 can be represented in hexadecimal is
.1 = .1999999 × 16
0
5. The exponent for the value is 3 (Step 2 above). To determine the actual exponent that
will be stored, take the exponent value and add the bias to it:
true exponent + bias = 3 + 40 = 43 (hexadecimal) = stored exponent
The final portion to be determined is the sign of the mantissa. By convention, the
sign bit for positive mantissas is 0, and the sign for negative mantissas is 1. This
information is stored in the first bit of the first byte. From the hexadecimal value in
Step 4, compute the decimal equivalent and write it in binary format. Add the sign
bit to the first position. The stored value now looks like this:
43 hexadecimal = (4 × 16
1
) + ( 3 × 16
0
) = 67 decimal = 0100 0003 binary
11000003 = 195 in d ecimal = C3 in hexadecimal
6. The final step is to put it all together:
4320019999999999 – floating point representation for 512.1
C320019999999999 – floating point representation for –512.1
Therefore, the decimal value 512.1 cannot be precisely represented in binary or
hexadecimal floating point notation. When the number 512.1 is converted, the result
is an infinitely repeating number. This is analogous to representing the fraction 1/3 in
decimal form.
The closest approximation is .33333333 with infinitely repeating ‘3s’.
This example shows how values that can be represented exactly in decimal notation
cannot always be represented precisely in floating-point notation. If a floating-point
value has a repeating pattern of numbers (like the above value has repeating ‘9s’), there
is a good chance that the value cannot be represented exactly.
Numerical Accuracy in SAS Software 71
Troubleshooting Errors in Precision
Computational Considerations
Regardless of how much precision is available, there are still some numbers that cannot
be represented exactly. Most rational numbers (for example, .1) cannot be represented
exactly in base 2 or base 16. This is why it is often difficult to store fractions in floating-
point representation.
Consider the IBM mainframe representation of
1: 40 19 99 99 99 99 99 99
Notice that here is an infinitely repeating 9 digit similar to the trailing 3 digit in the
attempted decimal representation of one-third (.3333 …). This lack of precision can be
compounded when arithmetic operations are performed on these values repeatedly.
For example, when you add .33333 to .99999, the theoretical answer is 1.33333, but
in practice, this answer is not possible. The sums become more imprecise as the values
continue to be calculated.
For example, consider the following DATA step:
data _null_;
do i=-1 to 1 by .1;
put i=;
if i=0 then put 'AT ZERO';
end;
run;
The AT ZERO message in the DATA step is never printed because the accumulation of
the imprecise number introduces enough errors that the exact value of 0 is never
encountered. The calculated result is close to 0, but never exactly equal to 0. Therefore,
when numbers cannot be represented exactly in floating point, performing mathematical
operations with other non-exact values can compound the imprecision.
Using the ROUND Function to Avoid Computational Errors
Errors that are caused by the accumulation of performing calculations on imprecise
values can be resolved by rounding. The following example shows how you can use the
ROUND function to round the results or make decisions for each iteration.
Example Code 4.7 Using the ROUND Function to Avoid Computational Errors
data _null_;
do i=-1 to 1 by .1;
i = round(i,.1);
put i=;
if i=0 then put 'AT ZERO';
end;
run;
72 Chapter 4 • SAS Variables

Log 4.2 Log Output for Using the ROUND Function to Avoid Computational Errors
i=-1
i=-0.9
i=-0.8
i=-0.7
i=-0.6
i=-0.5
i=-0.4
i=-0.3
i=-0.2
i=-0.1
i=0
AT ZERO
i=0.1
i=0.2
i=0.3
i=0.4
i=0.5
i=0.6
i=0.7
i=0.8
i=0.9
i=1
NOTE: DATA statement used (Total process time):
real time 0.01 seconds
cpu time 0.01 seconds
Here is another example of a numerical precision issue that occurs on z/OS but not on
the PC.
Example Code 4.8 Using the ROUND Function with the IF Statement
data a;
input gender $ height;
datalines;
m 60
m 58
m 59
m 70
m 60
m 58 ;
run;
proc freq;
tables gender/out=new;
run;
data final;
set new;
if percent=100 then put 'equal';
else put 'not equal';
run;
Numerical Accuracy in SAS Software 73
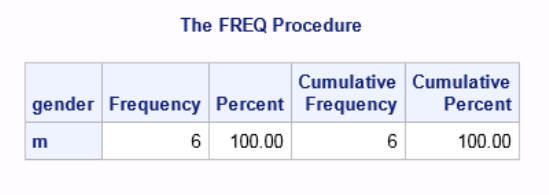
Output 4.6 Output for Using the ROUND Function with the IF Statement
In the example, PROC FREQ creates an output data set that contains the variable
Percent. Because all of the values for the variable Gender are the same, you might expect
Percent to have an exact value of 100. However, when the value of Percent is tested, the
log indicates that Percent is not exactly 100.
The algorithm used by PROC FREQ to produce the variable Percent involves
mathematical computations. The result is very close to 100 but not exactly. Using the
ROUND function (or the COMPFUZZ function) on the IF statement resolves this issue.
A work-around for very simple calculations (for example, retaining only 2 digits to the
right of the decimal point) is to multiply the values by 100 and use the ROUND function
to round them to integers. Once you have performed the calculations on the new whole
numbers, divide by 100 to convert the values back to decimal form.
In the following example, the values for variable x are stored in the SAS data set as real
numbers. The number is multiplied by 1,000 and the ROUND function is used to change
the values to integers. The SUM statement is used to sum all the values of
New. On the
last observation, which is detected using the END= option, the sum is divided by 1,000
to convert the values back to fractions.
Example Code 4.9 Summing Rounded Values
data a;
set b end=last;
new=round(x*1000);
sum+new;
if last then sum=sum/1000;
run;
See “ROUND Function” in SAS Functions and CALL Routines: Reference for more
information about this function.
Numeric Comparison Considerations
When comparing non-integer values that do not have precise decimal or hexadecimal
floating-point representations you can sometimes encounter surprising results. For
example, in decimal arithmetic, the expression
15.7 – 11.9 = 3.8
is true. But, in SAS, if you compare the literal value of 3.8 to the calculated value of
15.7 – 11.9 and output the result to the SAS log, you will get a result of 'not equal.'
Example Code 4.10 Comparing Values That Have Imprecise Representations
data a;
x=15.7-11.9;
if x=3.8 then put 'equal';
else put 'not equal';
run;
74 Chapter 4 • SAS Variables
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
