
Pattern Extraction Using Histogram ◾ 155
Figure 10.7 is a histogram of defects found per test case, a key metric in soft-
ware testing. e LSL has been set at 0.08, and the USL has been specified at 0.5.
Perhaps specifying a USL is unnecessary, but it is meant to cause an alert on prod-
uct quality in this case.
e lower limit is less controversial; the team expects a minimum return from
test cases. e target 0.3 defects found per test case is also marked for reference.
Visually, the histogram reveals capability-related issues: the process peak is not on
target, and a good deal of results (roughly 28%) fall below the lower specification
limit. e process has a lot to improve. e capability index is 0.26, much lower
than the desirable value of at least 0.8.
e test case metric “defects found per test case” is a double-edged sword. If
more defects are found, it could be either due to the poor quality of product on test
or highly effective test cases. If few defects are found, it could mean that the prod-
uct is good or the test cases are not effective. One has to appreciate both the pos-
sibilities and use extraneous evidence to judge the histogram.
Histogram as a Judge
ere is a very significant use of the histogram as a judge. First, it is a visual judge
of the normality of data. ere are debates about the normality of metric data, and
people do a normality test. A visual judgment of the histogram of the data can be a
first-order judgment of normality. If data are not normal, people do not do esoteric
statistical tests on the data.
Process data in software development is often nonnormal.
In these cases, the histogram is used to visualize data and to make a decision
about statistical tests. For example, time to repair data are avowedly nonnormal;
all known histograms testify to this. e problem is now escalated: one should use
nonparametric tests, or one should transform data appropriately and do statistical
tests. e author prefers the first. Let us keep data in its purest form.
ere is an area where we are sure data will have to be normal: prediction errors.
In any prediction model, errors are symmetric around the mean, and the mean
error value is zero. A histogram is of the errors usually plotted, to see if it is sym-
metrical around zero, to validate the prediction model.
Good regression models leave behind errors, or residuals, which are nor-
mally distributed and can be tested with histograms.
If the histogram is skewed, the model is not accepted and needs to be improved.

156 ◾ Simple Statistical Methods for Software Engineering
From One Point to One Histogram
To judge a process or a product, a single observation is not enough. We need mul-
tiple observations and a histogram constructed out of the multiple observations.
e minimum element in statistical structure seems to be a histogram. If we have to
judge a process, we need to make enough observations and plot a process capability
histogram. If we have to study product behavior, we need to collect enough data
from a minimum number of modules and construct a histogram. Both the process
and the product can be observed only through histograms.
Case Study: Goal Entitlement
Setting stretch goals is a tricky challenge. Such goals have to be realistic too. e
goal setting process must be transparent as well. is case study presents the use of
histograms in setting stretch goals.
Productivity analysis using histogram reveals the presence of two clusters. e
stronger peak seems to be of higher productivity. e smaller cluster is closer to the
present goal of 50 lines of code (LOC) per day.
ere is every reason to increase the goal to the best practice cluster peak,
marked B, following a natural path of improvement shown in Figure 10.8.
Entitlement is the best you can possibly operate without redesigning your
process. It is the dierence between the current level of performance and the
best documented.
is is the core concept in “goal entitlement.” A conservative stretch goal will be
to set any intermediate point C on the path of improvement such that 70% of the
ideal improvement is targeted. us, C becomes a new goal. With the histogram
in the background, the entire analysis and planning is data based and realistic and
makes it easy for people to accept the stretch goal without any reservation.
BOX 10.4 WEB CONTENT EXTRACTION
e content of web pages is extracted by using the HTML document’s Text-
To-Tag Ratio histograms. Web content extraction is seen as a histogram clus-
tering task. Histogram clustering is a widely researched topic that is especially
popular with image researchers. is is especially true among researchers who
wish to use the histogram footprints of images as a means for classification,
segmentation, etc. ese clustering techniques are also enhanced with the use
of histogram smoothing techniques. High recall and precision are achieved
by this technique. (Weninger and Hsu [8])

Pattern Extraction Using Histogram ◾ 157
Goal entitlement is contested by some, as in e Entitlement Trap by Dennis J.
Monroe [9]. He argues, “Goal setting by entitlement does not quantify opportunity
for breakthrough improvement.”
BOX 10.5 A STUDY OF REUSE
e benefits of software reuse range from decreased development time and
increased product quality to improved reliability and decreased maintenance
costs. e amount of reuse is measured by several metrics. Curry et al. [10]
focused on three metrics:
1. Reuse level (RL): It measures the ratio between different lower level
items reused verbatim inside a higher level item versus the total number
of lower level items used.
2. Reuse frequency (RF): It measures the number of references to reused
items rather than counting items only once, as was performed for the
reuse level. is metric measures the percentage of references to lower
level items reused verbatim inside higher level items versus the total
number of reference.
Present
goal
Best
practice
Improvement
path
A
B
C
120
100
80
60
40
20
0
30
35
45
40
55
50
65
60
75
70
85
80
95
90
105
100
115
110
Productivity, LOC per day
Frequency
Figure 10.8 Histogram representing an improvement path.
158 ◾ Simple Statistical Methods for Software Engineering
Appendix 10.1: Creating a Histogram
ere are a few standard steps used in histogram creation. We are using the Excel–
Data–Data Analysis–Histogram option.
Data are made available as a column. Column A in Figure A10.1 contains cou-
pling data between objects. Many objects seem to be self-contained but quite a few
are coupled (Data A10.1).
3. Reuse density (RD): It measures how much reuse is in a product with
respect to the size of the product. It is the ratio of total number of lower
level items reused inside a higher level item normalized to the size of the
higher level item.
e question is if the three metrics are redundant. To solve the problem,
the authors have used histograms of correlations. e analysis shows interest-
ing findings with statistical confidence made available by histograms. Instead
of using an average level of correlation, the authors have preferred histogram
expressions of correlations. ey conclude,
It is evident that from a statistical point of view in the considered C
projects, RL and RF measure very similar properties of the code, while
RD presents an independent perspective on the amount-of-reuse.
Just two metrics are enough to manage reuse.
0.00%
20.00%
40.00%
60.00%
80.00%
100.00%
120.00%
0
2
4
6
8
10
12
0 2.2 4.4 6.6 8.8 More
Frequency
Bin coupling
Frequency
Cumulative %
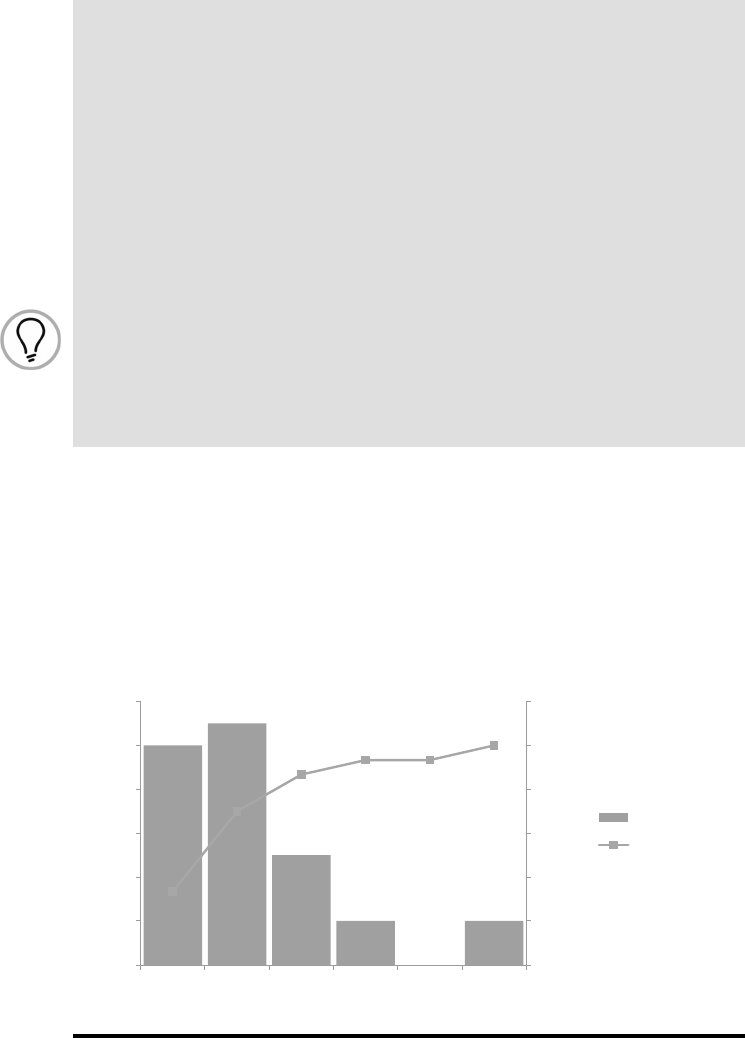
Figure A10.1 Histogram and ogive (cumulative %).

Pattern Extraction Using Histogram ◾ 159
We run the tool Histogram. Define the input range and select the option for
chart output and cumulative percentage. Take the report from Excel by specifying
“output range.” Table A10.1 and Figure A10.1 show the histogram of coupling and
the cumulative curve, known as ogive. Select tally columns Bin and Frequency and
plot an XY scatter diagram to obtain Figure A10.2. is figure is a smoothened
profile of the histogram.
Interpretation
e coupling histogram is skewed to the right. e tendency of developers seems
to produce less complex classes. at is a very good sign. ere seems to be a few
high complex outlier classes. is appears as a small independent bar on the right.
Data A10.1 Coupling Data
1
10
2
3
2
3
2
1
1
2
0
0
1
0
3
0
4
0
2
0
5
0
2
0
6
0
11
0
4
1
Table A10.1 Tally
Bin Frequency Cumulative %
0 10 33.33
2.2 11 70.00
4.4 5 86.67
6.6 2 93.33
8.8 0 93.33
More 2 100.00
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
