
168 ◾ Simple Statistical Methods for Software Engineering
2. Negative binomial distribution
Negative binomial distribution (NBD) is defined by the probability of get-
ting k successes until r failures occur, given by the following expression:
P X k C p p
k
r k k r
( ) ( )= = −
+ −1
1 (11.4)
where n is the number of trials, p is the probability of success (same for each trial),
k is the number of successes observed in n trials, and r is the number of failures.
Mean =
−r p
p
( )1
(11.5)
Variance =
−r p
p
( )1
2
(11.6)
If k remains as an integer, the distribution is sometimes known as the Pascal
distribution. Many engineering problems are elegantly handled with NBD.
In sampling, if the proportion of individuals possessing a certain charac-
teristic is p and we sample until we see r such individuals, then the number of
individuals sampled is a negative binomial random variable.
e NBD is one of the most useful probability distributions. It is used to
construct models in many fields: biology, ecology, entomology, and informa-
tion sciences [2].
Example 11.2: NBD of Right First-Time Delivery
QUESTION
In a network sensor manufacturing division, the right first-time rate is 0.6. e
company wants to deliver 10 sensors to a mission critical application and prefers to
ship after choosing from the right first-time lot. What is the probability of deliver-
ing 10 right sensors produced for the first time if the production batch size is 12?
Plot the negative binomial probability distribution function associated with this
problem. Calculate the mean and variance of the distribution.
ANSWER
It may be seen that data can be represented in Equation 11.4 with the following
parameters:
r = 10 number of successes
p = 0.6 probability of success
k = n − 10 number of failures
n = production batch size, 10, 11, …
We can use the Excel function NEGBINOM.DIST to generate the NBD and
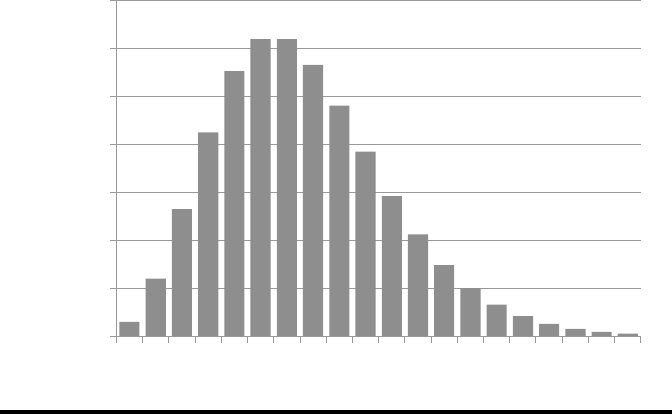
plot the graph, as shown in Figure 11.2.
The Law of Large Numbers ◾ 169
e Excel function appears as follows, with four arguments:
NEGBINOM.DIST(number_f, number_s, probability_s, cumulative)
where number_f is the number of failures (k in NBD Equation 11.4), number_s is the
threshold number of successes (r in NBD Equation 11.4), probability_s is the probabil-
ity of success (p in NBD Equation 11.4), and cumulative is a logical value that deter-
mines the form of the function. If cumulative is true, NEGBINOM.DIST returns the
cumulative distribution function; if false, it returns the probability density function.
Finding the probability of delivering 10 right sensors produced for the first
time from a batch of size 12 can be directly solved as follows:
Batch size n = 12
Number of success s = 10
Number of failure k = 2
Probability of success p = 0.6
e Excel function returns the answer 0.0532. us, there is only a small
chance of finding 10 right sensors produced for the first time.
e mean and variance of the NBD can be directly computed by entering data
in Equations 11.5 and 11.6. e answers are as follows:
Mean = 15
Variance = 37.5
Figure 11.2 shows that the sensor problem peaks at the mean.
0
0.02
0.04
0.06
0.08
0.10
0.12
P(X = k) = C
k
p
k
(1 – p)
r
0.14
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
Probability
Trials, n = k + r
r+k–1
Figure 11.2 Negative binomial for right first time delivery (r = 10, success prob-
ability p = 0.6).

170 ◾ Simple Statistical Methods for Software Engineering
3. Geometric distribution
e probability k of Bernoulli trials needed to obtain one success is given
by the following expression:
P X k p p
k
( ) ( )= = −
−
1
1
(11.7)
where p is the probability of success (same for each trial) and k is the number
of successes observed in n trials.
Mean =
1
p
(11.8)
Variance =
−1
2
p
p
(11.9)
Example 11.3: Geometric Distribution
QUESTION
e right first-time design probability in a software development project is esti-
mated at 0.7. Estimate the probability of needing four trials to find a defect-free
feature design. Plot a graph between trials and geometric probability.
ANSWER
In this problem, p = 0.7 and k = 4.
Inserting these values in Equation 11.3, we obtain the geometric probability
(0.0189).
Figure 11.3 shows the graph.
4. Hypergeometric distribution
e hypergeometric distribution is a discrete probability distribution that
describes the probability of k successes in n draws without replacement from
a finite population of size N containing exactly K successes. is is given by
the following equations:
P X r
C C
C
r
K
n r
N K
n
N
( )= =
−
−
(11.10)
Mean = n
K
N
(11.11)
Variance =
−
−
−
n
N K
N
N n
N 1
(11.12)

The Law of Large Numbers ◾ 171
Example 11.4: Hypergeometric Probability
QUESTION
A release of 10 modules has just been built and the smoke test is over. Results
show that there are four defective modules. If we draw samples of size 3 with-
out replacement, find the probability that a sample contains two defective
modules.
ANSWER
First, we assume that the proportion of defective modules follows the law of aver-
ages and holds good for every module. Given the fact that smoke tests do not find
all defects, such an assumption has serious implications. However, to go ahead
with solution formulation, we proceed with the following assumption:
You can solve Equation 11.4 by substituting N = 10, K = 4, n = 3, and r = 2
Alternatively, use Excel statistical function HYPGEOM.DIST to solve
Equation 11.4. e data entry window must be filled as follows:
Sample_s Number of successes in the sample Enter 2
Note: Success in a statistical sense is finding a defective module. Testers also share
this view.
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1 2 3
Geometric probability
4 5 6
k
7 8 9 10
p = 0.7
Figure 11.3 Geometric probability distribution for defect free design.

172 ◾ Simple Statistical Methods for Software Engineering
Number_sample Size of the sample Enter 3
Population_s Number of successes in the population Enter 4
Number_pop Population size Enter 10
Cumulative Logical value that determines the form of the function. Enter false
If cumulative is true, then HYPGEOM.DIST returns
the cumulative distribution function; if false, it returns
the probability mass function.
Excel returns the following answer: formula result = 0.3.
us, the probability that a sample of three modules contains two defective
modules is 0.3.
Plots of Probability Distribution
To plot the PDF of hypergeometric probability, two scenarios are considered. e
first is an inquiry into the chance of all items in the sample being defective. Figure
11.4a presents a plot between sample size and hypergeometric probability. e sec-
ond is a study of one item in a sample being defective. Figure 11.4b presents the plot
between sample size and hypergeometric probability.
0
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
1 2 3 4 5 6
Sample size
Sample size
0
0.1
0.2
0.3
0.4
0.5
0.6
1 2 3 4 5 6 7 8 9 10
Probability
Probability
(a)
(b)
Figure 11.4 (a) Hypergeometric probability of all items in a defective sample
(N= 10, K = 4). (b) Hypergeometric probability of one sample in a defective
sample (N = 10, K = 4).
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
