
Weibull Distribution ◾ 309
Deliveredreliability
= WeibullCDF(40)
ExcelsyntaxforCDF
= Weibull (40,1,20,1)
=0.98
0
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
0.65
0.70
0.75
0.80
0.85
0.90
0.95
1.00
1.05
1.10
1.20
1.15
10 20 30 40 50
Release
date
Project days
Cumulative defects discovered
α = 2
β = 20
Delivered
reliability
60 70
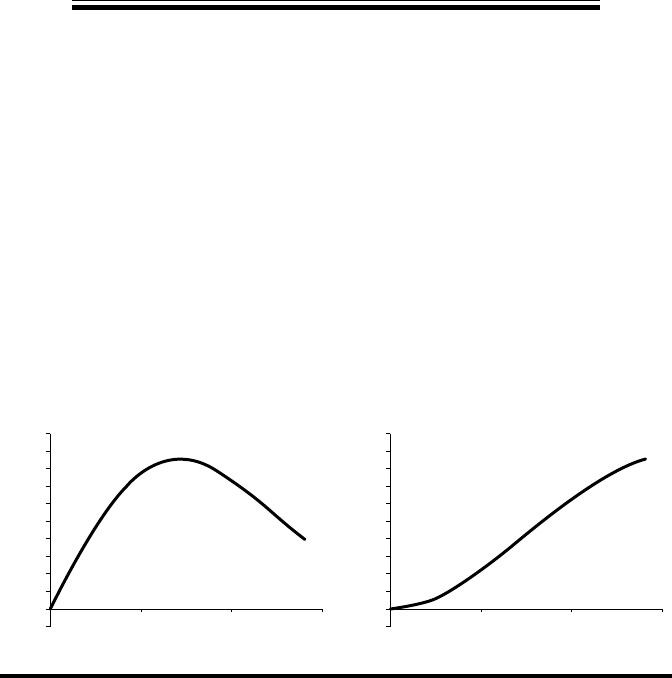
Figure 19.7 Weibull distribution CDF—delivered reliability.
Residual
defects
α = 2
β = 20
0
0.00
0.005
0.010
0.015
0.020
0.025
0.030
0.035
0.040
0.045
0.050
10 20 30 40
Project days
Defects discovered
50 60 70
Figure 19.6 Weibull distribution—defect discovery model.

310 ◾ Simple Statistical Methods for Software Engineering
shown that the dynamics of the nonoperational testing processes translates into a
Weibull failure detection model. Vouk also equated the Weibull model (of the sec-
ond type) into the Rayleigh model. He affirmed that the progress of the nonopera-
tional testing process can be monitored using the cumulative failure profile. Vouk
illustrated and proved that the fault removal growth offered by structured based
testing can be modeled by a variant of the Rayleigh distribution, a special case of
the Weibull distribution.
In a novel attempt, Joh et al. [9] used Weibull distribution to address security
vulnerabilities, defined as software defects “which enables an attacker to bypass
security measures.” ey have considered a two-parameter Weibull PDF for this
purpose and built the model on the independent variable t, real calendar time. e
Weibull model has been attempted on four operating systems. e Weibull shape
parameters are not fixed at around 2, as one would expect; they have been varied
from 2.3 to 8.5 in the various trials. It is interesting to see the Weibull curves gen-
erated by shapes varying from 2.3 to 8.5. In Figure 19.8, we have created Weibull
curves with three shapes covering this range: 2.3, 5, and 8.5.
Tai et al. [10] presented a novel use of the three-parameter Weibull distribu-
tion for onboard preventive maintenance. Weibull is used to characterize system
components’ aging and age-reversal processes, separately for hardware and soft-
ware. e Weibull distribution is useful “because by a proper choice of its shape
param eter, an increasing, decreasing or constant failure rate distribution can be
obtained.” Weibull distribution not only helps to characterize the age-dependent
failure rate of a system component by properly setting the shape parameter but also
allows us to model the age-reversal effect from onboard preventive maintenance
using “location parameter.” Weibull also can handle the service age of software and
the service age of host hardware. ey find the flexibility of the Weibull model very
valuable while making model-based decisions regarding mission reliability.
–0.5 0.0 0.5 1.0
x
Weibull probability
1.5
Location
=
0 alpha
=
2.3 beta
=
1
Location
=
0 alpha
=
5 beta
=
1
Location
=
0 alpha
=
8.5 beta
=
1
2.0 2.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
Figure 19.8 When Weibull shape factor changes from 2.3 to 8.5.

Weibull Distribution ◾ 311
Putnam’s Rayleigh Curve for Software Reliability
Remembering that the Rayleigh curve is similar to the Weibull Type II distribu-
tion, let us look at Lawrence Putnam’s Rayleigh curve, as it was called, for software
reliability:
E
E
t
te
m
r
d
t
t
d
=
−
6
2
3
2
2
(19.8)
MTTD after milestone 4=
1
E
m
where E
r
is the total number of errors expected over the life of the project; E
m
is the
errors per month; t is the instantaneous elapsed time throughout the life cycle; t
d
is
the elapsed time at milestone 7 (the 95% reliability level), which corresponds to the
development time; and MTTD is the mean time to defect.
To apply this curve software, the life cycle must be divided into nine milestones
as prescribed by Putnam and define the parameters by relating them to the relevant
milestones [11,12]. ere are many assumptions behind this equation. is model
works better with large full life cycle projects that follow the waterfall life cycle
model. Putnam claimed,
With this Rayleigh equation, a developer can project the defect rate expected
over the period of a project.
Cost Model
Putnam used the same Rayleigh curve to model manpower build up and cost dur-
ing the software development project. e equation was used in his estimation
model. e same equation was used to define productivity. Putnam’s mentor Peter
Norden had originally proposed the curve in 1963. Putnam realized its power and
applied it well. e equation came to be known popularly as the software equation.
Technically, it is known as the Norden–Rayleigh curve.
Putnam recalls [11],
I happened to stumble across a small paperback book in
the Pentagon bookstore. It had a chapter on managing R&D
projects by Peter Norden of IBM. Peter showed a series of
312 ◾ Simple Statistical Methods for Software Engineering
curves which I will later identify as Rayleigh curves. These
curves traced out the time history of the application of
people to a particular project. It showed the build up, the
peaking and the tail off of the staffing levels required to get
a research and development project through that process
and into production. Norden pointed out that some of these
projects were for software projects, some were hardware
related, and some were composites of both. The thing that
was striking about the function was that it had just two
parameters. One parameter was the area under the curve
which was proportional to the effort (and cost) applied, and
the other one was the time parameter which related to the
schedule.
Defect Detection by Reviews
Defect detection by reviews can be modeled by using the Weibull curve. Typically,
we begin with a shape factor of 2, the equivalent of the Rayleigh curve.
Figure 19.9 shows a typical Weibull model for review defects. e cumulative
curve ends at 0.86, before becoming flat. is roughly indicates that 14% of defects
are yet to be uncovered, but the review process has been stopped beforehand. e
PDF is clearly truncated.
At a more granular level, the review defect Weibull model can be applied to
requirement review, design review, code review, and so on. It is cheaper to catch
defects by review than by testing, and using such models would motivate reviewers
to spend extra effort to uncover more defects.
0.0
–0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.5 1.0
Time
Defects detection
1.5 0.0
–0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.5 1.0
Time
Cumulative defects found %
1.5
Figure 19.9 Weibull curve of family 2 showing premature closure of review.

Weibull Distribution ◾ 313
New Trend
e defect discovery performance of contemporary projects may be seen to be dra-
matically different from the traditional models. In a recent data benchmark done
by Bangalore SPIN (2011–2012), a consolidated view of the defect curves across
eight life cycle phases is presented. A summary is available for public view in their
website bspin.org, and a detailed report can be obtained from them.
BSPIN reports two types of defect curves coming from two groups of projects
shown in Figure 19.10.
In one group, the unit test seems to be poorly done, and the defect curve is not
a smooth Rayleigh but broken. It looks as if the first defect discovery process ends
and another independent defect discovery process starts during later stages of test-
ing. e defect curve is a mixture. As a result, the tail is fat, much fatter than the
homogeneous Rayleigh (Weibull II) would be able to support. In the second group
unit, the test was performed well and the defect curve had no tail. Again, the defect
curve with abruptly ending slope is not the unified Putnam’s Rayleigh.
We may have to look for a special three-parameter Weibull with unconven-
tional shape factors to fit these data. Both the curves affirm that a new reality is
born in defect management. ere is either a low maturity performance where the
testing process shows a disconnect resulting in postrelease defects or a high matu-
rity process with effective early discovery that beats the Rayleigh tail: a mixture
curve with double peak or a tailless curve. In the first case, the vision of a smooth,
unified, homogeneous and disciplined defect discovery has failed. In the second
case, defect discovery technology has improved by leaps and bounds, challenging
the traditional Rayleigh curve.
Bestpractice
Project group II
Project group I
REQ
0.00
5.00
10.00
15.00
% Mean defects found
20.00
25.00
30.00
HLD DLD Code
review
UT IT ST Postrelease
Figure 19.10 Defect distribution across project lifecycle phases.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
