290 ◾ Simple Statistical Methods for Software Engineering
If there is a tolerance limit for clarification time set at 80 days by the main-
tenance team, then we can mark a line at x = 80 at the PDF. is line defines a
tail, whose area represents risk. is line is marked in Figure 18.4. is is a fat tail
indeed, indicating high risk. We have chosen gamma distribution to produce this
fat tail and capture the hidden risk loud and clear.
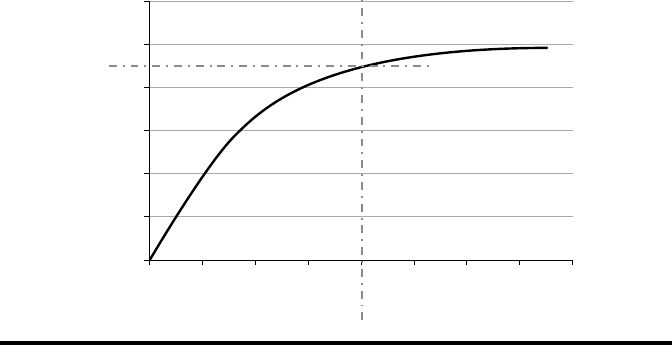
To judge risk, we better plot the cumulative gamma distribution for the same
scale and shape parameters. is CDF is shown in Figure 18.5.
e line from the tolerance limit of 80 days meets the CDF, and from the
meeting point, a horizontal line is drawn, which meets the y axis at around 0.9.
e y axis represents cumulative probability, and 0.9 means that there is a 90%
chance of clarification time being within the limit. e risk of exceeding the limit
is therefore 10%.
Shifting the Gamma PDF
Assume that the customer specifies a minimum time they need to resolve this prob-
lem, given the fact that the related managers are constantly traveling and com-
munication with them slows down. Assume further that the customer specified a
minimum of 4 days. Building this minimum time into the gamma function means
“shifting of the curve” to the right by 4 units of time, as shown in Figure 18.4. at
means that the location of the curve is shifting from x = 0 to x = 4. is minimum
defines the location parameter μ.
0 20 40 60 80
Clarification time (days)
Probability
100 120 140 160
0
0.2
0.4
0.6
0.8
1
1.2
Figure 18.5 Gamma cumulative distribution of clarification time with a shape of
1.2 and a scale of 30.1352.

Gamma Distribution ◾ 291
With the inclusion of a location parameter μ, the gamma PDF equation experi-
ences a change. e change is realized by substituting in Equation 18.1 (x − μ) in
the place of x. After the inclusion of μ, the new equation of the shifted gamma PDF
is given as follows:
G x x e x
x
( )
( )
( ) ;= − > >
−
−
−
1
0
1
β α
µ µ α β
α
α
µ
β
Γ
, (18.4)
Generating Clarification Time Scenarios with
Gamma PDF Built from Minimal Data
e three-parameter gamma function in Equation 18.4 retains the properties of the
two-parameter version. Equations 18.2 and 18.3 are still relevant.
Let us try to use the gamma PDF defined in Equation 18.4 to model clarifica-
tion time by the customer for three possible scenarios in a maintenance project.
Box 18.2 inventor of Gamma diStriBution
Leonhard Euler (1707–1783), one of the greatest mathematicians of all time,
is credited with the discovery of gamma function. Some say his teacher,
Bernoulli, another mathematician, invented it first.
Euler was born in Switzerland, in the town of Basel. At 13 years of age,
Euler was already attending lectures at the local university. In 1723, he gained
his master’s degree, with a dissertation comparing the natural philosophy sys-
tems of Newton and Descartes. He wrote two articles on reverse trajectory,
which were highly valued by his teacher Bernoulli.
At this time, a new center of science had appeared in Europe—the
Petersburg Academy of Sciences. As Russia had few scientists of its own,
many foreigners were invited to work at this center, among them Euler. On
May 24, 1727, Euler arrived in Petersburg.
Euler took a very active role in the observation of the movement of Venus
across the face of the sun, although at this time he was nearly blind. He had
already lost one eye in the course of an experiment on light diffraction in
1738, and an eye disease and botched operation in 1771 led to an almost total
loss of vision.
However, this did not stop Euler’s creative output. Until his death in 1783,
the academy was presented with more than 500 of his works. e academy
continued to publish them for another half century after the death of the
great scientist. To this day, his theories are studied and taught, and his incred-
ibly diverse works make him one of the founding fathers of modern science.

292 ◾ Simple Statistical Methods for Software Engineering
Our knowledge of existing pattern and the gamma parameters we have derived
from existing data are very relevant clues for this model.
Let us begin with an assurance given by the customer to reduce the mean clari-
fication time from the current 36.16 days to 20 days. e customer has already
declared that he needs a minimum of 4 days for clarification. ese two numbers,
4 and 20, represent the two agreed performance levels as declared by the customer,
the minimum and the mean. ese are really minimal data gathered to characterize
clarification time. Gamma distribution will do the rest and fit behavioral details
into the model based on known patterns.
Where data are minimal, gamma distribution lls the gap.
e minimum value 4 represents the location parameter, a fixed value in the models
we are going to build.
We construct three types of customer responses defined by gamma with three
values for shape factors: 1.2, 2.0, and 3.0. is selection is intuitive and is based on
familiarity and knowledge of maintenance teams of customer behavior as well as of
gamma distribution shapes.
With the help of Equation 18.2, we can estimate the scale parameter as follows:
Corresponding to the shape factor 1.2, the scale factor is = mean/1.2 = 20/1.2 = 16.67.
Corresponding to the shape factor 2.0, the scale factor is = mean/2.0 = 20/2.0 = 10.
Corresponding to the shape factor 3.0, the scale factor is = mean/3.0 = 20/3.0 = 6.67.
Agreeing to the two customer suggestions, now the maintenance team has to pre-
dict expected variations in customer response by applying the gamma PDF.
ree sets of gamma parameters, the scale and the shape factors, set the theater
for simulation. e values of μ, α, and β for the three scenarios are as follows:
Scenario I gamma [4, 1.2, 16.67]
Scenario II gamma [4, 2.0, 10.00]
Scenario III gamma [4, 3.0, 6.67]
e three gamma distributions, depicting the three scenarios, are plotted in
Figure 18.6.
Modes
It may be seen that each scenario has a distinctly unique mode. e modes are 7, 14,
and 17 days. is means that according to Scenario I, the customer is most likely
to resolve clarification queries in 7 days. According to Scenario II, the most likely
clarification time is 14 days. According to Scenario III, the most likely clarification
time is 17 days. ese modes represent the most visible customer performance. e
modes represent performance highlights.

Gamma Distribution ◾ 293
Tails
In Figure 18.6, a tolerance limit is specified as 50 days. is limit marks the end
of core performance and the beginning of the tail area. Area beyond the tolerance
limit is the risk associated with the chosen gamma scenario.
Risks (%) in the three scenarios are 8.68, 5.40, and 3.03 from the tail areas of
Figure 18.6. ese risks have been computed by dividing the tail area by the total
area.
Box 18.3 Gamma modelinG of rainfall
Gamma distribution is often used in rainfall modeling.
In water resource projects, it is necessary to collect all the information
related to the region and then to analyze the collected data. A frequency analy-
sis of the rainfall data is the most commonly applied method. e hydrologist
searches for a mathematical equation characterizing the available data in hand,
to fill the gaps in the observations and to extrapolate it to a longer period.
Typically, two-parameter gamma distributions are fitted to rainfall data.
e shape and scale parameters of the gamma distribution, α and β, are deter-
mined from the daily rainfall data of the gauging station.
Minimum time
required by
customer
Mean, agreed
by customer
Loc = 4 shape = 1.2 scale = 16.67
Loc = 4 shape = 2 scale = 10
Loc = 4 shape = 3 scale = 6.67
Tolerance
limit
0
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
10 20 30 40
Clarification time (days)
50 60 70
Figure 18.6 Gamma scenarios of clarification time.

294 ◾ Simple Statistical Methods for Software Engineering
Scenario Analysis
e gamma model enables us to evaluate three scenarios, three kinds of responses,
from the customer. e first response has a shorter mode of 7 days but a higher risk
of 8.68%. is could happen if the customer is requested to provide earlier response
as a top priority.
e second response has a mode of 14 days but a lower risk of 5.4%. Judging
by the apparent central tendency, mode, the customer seems to have slowed down,
but the overall risk has reduced in a counterintuitive way.
In the third scenario, perhaps the customer is in his element, the mode is
delayed further and reached a value of 17 days while the overall risk has come down
further to a low value of 3.03%.
e tricky balance between demonstrated mode and real risk is a lesson we
learn from this study.
Like in the case of customer clarification time in maintenance projects, gamma
models can be built for internal clarification time taken by developers to respond to
queries from testers in during software development. Gamma models can also be
built for requirements elicitation time in software development. In all these cases,
the gamma lesson can be applied:
Early closure is a myth; closure needs a natural time for understanding,
analysis, training, and response.
Different techniques are used in estimating the parameters: the graphical
method, the least squares method, the method of moments, and the maxi-
mum likelihood method.
In the analysis of 30 years of rainfall data, it is seen that α varies between
0.341 and 0.569 and β varies between 6.892 and 19.94 in a year. ese
gamma distribution parameters summarize the pattern of rain fall (based on
Aksoy [3]).
Box 18.4 PaCkinG hiStory into a
Gamma Pdf with minimal data
Rainfall data can be huge, especially when one wants to study history. Presenting
descriptive statistics such as maximum, minimum, mean, median, and variance
is still not adequate. Climatologists prefer to fit mathematical models such as
gamma distribution to represent the overall pattern. Descriptive statistics and
more are inherent in the equation. All that is required is just two parameters—
the shape and scale parameters—for a season and location.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
