11

Arbitration

11.1 INTRODUCTION

Arbitration circuits, or simply arbiters, are commonplace in digital systems where a restricted number of resources are allocated to different user or client processes. Typical examples are systems with shared busses, multi-port memories, and packet routers, to name but a few. The problem of arbitration between multiple clients is particularly difficult to solve when it is posed in asynchronous context, where the time frames in which all clients operate may be different and vary with time. Here, the decision which resource is to be given to which process must be made not only on the basis of some data values, such as priority codes or ‘geographical’ positions of the clients, but also depending on the relative temporal order of the arrival of requests from the clients. In a truly asynchronous scenario, where no absolute clocking of events is possible, the relative timing order cannot be determined by any means other than making the arbiter itself sense the request signals from the clients at the arbiter's inputs. This implies the necessity to use devices such as synchronizers (Sync) and mutual exclusion (MUTEX) elements, described in previous chapters. Such devices have the required sensing ability because they operate at the analog level and they could be placed at the front end of the arbiter.

Why does the problem of arbitration need to be considered in asynchronous context? Can we build a clocked arbiter, in which the clock would tell the rest of the circuit when it should allocate the resources? If we attempt to answer these questions positively we will immediately run into an infinite implication. Namely: who will clock the arbiter? Who will synchronize the clock with the rest of the arbiter? Who will clock the synchronizer (which is an arbiter itself!) between the clock and the rest of the arbiter? And so on.

The problem of designing systems with arbitration requires the designer to clearly understand the behaviour of typical arbiters in their interaction with clients and resources. Moreover, in order to design a new arbiter the designer should come up with a formal specification of the arbiter, by defining its architecture and algorithm, to be able to verify its correctness and possibly synthesize its logic implementation. This kind of task requires an appropriate description language, which should be capable of describing the various dynamic scenarios occurring in the overall system in a compact and functionally complete form. Unfortunately, traditional digital design notations such as timing diagrams, although adequate for simple sequential behaviours cannot easily capture asynchronous arbitration in a formally rigorous and precise way. Such behaviour can be inherently concurrent, at a very low signalling level, and may involve various kinds of choice, both deterministic and nondeterministic. In this chapter we are going to use Petri nets [78,79] and their special interpretation called signal transition graphs (STGs) [80,81] to describe the behaviour of arbiters. This modelling language satisfies the above-mentioned requirements. First attempts to use Petri nets and STGs in designing arbiters have been presented in [82,83].

Using Petri nets and STGs in describing arbiters enables the designer not only to trace the behaviour of the circuits, but also perform formal verification of their correctness, such as deadlock and conflict detection, as well as logic synthesis of their implementations. In this Part we do not consider these tasks focusing mostly on the architectural aspects of designing and using arbiters. However, we are currently working on a formal methodology for designing arbiters from Hardware Description Language specifications [84], where we are building on the initial ideas for synthesis presented in [85,86].

11.2 ARBITER DEFINITION

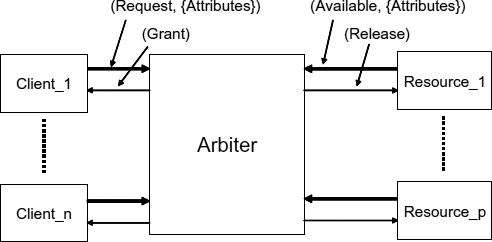
Let us start with a conceptual definition of arbiter. From a fairly general point of view, an arbiter has a set of input request channels that come from the clients which request resources, and it allocates resources by activating a set of output resource channels, each of which is associated with the provision of resources (Figure 11.1). The aim is to optimally match the resources requested with the resources available over a period of time.

Figure 11.1 Synopsis of an arbiter.

The channels are subdivided further to signals, bearing in mind the asynchronous nature of protocols in which the arbiter interacts with its clients and resources. A particularly important role is given to handshake schemes, based on request/acknowledgement pairs of signals which will be defined in detail in the next section. For example, each request channel has a ‘request’ signal to the arbiter which indicates that resources are required and a ‘grant’ signal that is returned to the client when the resources requested are available. The request channel may also be equipped with some input data, ‘request attributes’, which indicate the priority of the request, and the type and amount of resources required (Figure 11.1). The data inputs are not allowed to change between request and grant.

Each resource channel has an input ‘resource available’ signal to indicate that the resource can be acquired by a client and an output ‘release’ signal which indicates the release of the resource by a client. The resource channel may have some input data, ‘resource attributes’, containing the characteristics of the resource available, such as for example the performance and capacity of the resource as some may be faster and larger than others (Figure 11.1). Again, the data must not change between resource available and release of the resource.

Therefore, informally, an arbiter is some sort of a dynamic ‘matchmaker’ between clients and resources which may follow some policy in making the matches. For example, in order to allow for fairness the arbiter may be required to be able to compute the number of requests granted from each input request and the number of output resource grants over a period of time. The arbiter can then ensure that the ratio between these counts is within certain limits for each client. How this is done is defined by the detailed behavioural description of the actual arbiter and its internal architecture, e.g. ring, tree, etc. At the algorithmic level, we may only allow one arbitration action between requests and resources active at one time, or we may have concurrency in the case of multiple resources so that groups of resources in a network could perhaps be allocated to competing clients while others are still active.

11.3 ARBITER APPLICATIONS, RESOURCE ALLOCATION POLICIES AND COMMON ARCHITECTURES

Examples of arbitration phenomena can be found at all levels of computing systems. In software for example, operating systems apply various mechanisms to synchronize processes in concurrent environments, the most well-known being E. Dijkstra's semaphores. A semaphore is a shared variable whose value can be tested and modified by several processes. Depending on the value the testing process may be admitted to a critical section of the code. Processes act as clients and critical sections act as resources. Semaphores, together with the software (or hardware) maintaining their test and modify operation, act as arbiters. On the other hand a semaphore variable itself, together with its operations, can be treated as a resource which needs protection in the form of another arbitration mechanism, implemented at the lower level of abstraction. At some level this recursive mutual exclusion problem has to be resolved by processor hardware. In the world of true concurrency where the processes are mutually asynchronous, e.g. some of them associated with peripheral devices, the problem is ‘solved’ by means of an interrupt mechanism that implements a set of binary signals, i.e. flip-flops, which record interrupt signals. There is a necessary element in processing interrupt signals, namely the method with which they are ‘frozen’ for processing. At the time when the interrupt signals are processed, their status and their data attributes must be stable to avoid hazards.

Having multiple layers of software deferring the ultimate conflict resolution down to the lower level is one possibility. However, in many cases, and particularly with developments in the area of systems-on-chip, one should seriously think about complex resource allocation procedures implemented directly in hardware. A typical example of arbitration at the hardware level would be a router or switch, say between processors and memory blocks, which has a number of input channels (clients) and output channels (resources) with a certain resource allocation mapping. For example, let the switch have three input channels, IC1, IC2 and IC3, and two output channels, OC1 and OC2. Let the allocation mapping be such that a request on IC1 requires use of OC1, IC2 on OC2, but a request on IC3 requires both OC1 and OC2.

In addition to resource allocation mapping, which does not say much about the fairness of resource allocation, there may also be fairness policies. A fairness policy may often be completely independent of the allocation mapping, but may also reflect the fact that certain mappings need more careful fairness policies. The issue of fairness is closely related with that of priority in the system. It arises when a number of requests can be served from the point of view of the allocation mapping, but the mutual exclusion conditions forbid granting them all. For example, in the above case, if only requests on IC1 and IC2 arrive, they can be served in parallel because there is no conflict between them on the required resources, OC1 and OC2, respectively. Similarly, if only an IC3 request arrives, it can be granted both OC1 and OC2. On the other hand, if all three requests arrive together, there may be an argument about unfairness to IC3. Indeed, because the requests may arrive not simultaneously, but with a small time difference, there is often a chance that the system may favour requests on IC1 and IC2 more than IC3. The reason for that is that the probability of the resources OC1 and OC2 being both free at the same time is much less than that of either of them being free, which implies the natural preference of the system towards IC1 and IC2, who need less resources, and may enter a mode where they alternate and leave IC3 starving. In order to affect the allocation policy, defined by the allocation mapping, one can introduce the notion of priorities which can exhibit themselves in different forms [87].

One typical form is a geographical position of the clients with respect to the arbiter which is built as a distributed system. The famous ‘daisy-chain’ arbiter, in which the requests of the clients are assumed to require only one resource are polled in a linear order, always starting from the same source position, has a fixed and linear priority discipline. Here the nearer the request to the source the higher its priority. Alternatively, one can apply a round-robin discipline in a ring-based architecture and launch one or more special ‘tokens’ associated with the resources. Each request can collect appropriate tokens, without releasing them until all of them are in possession so the grant can be issued. In this case, regardless of the relative position of the request, we can guarantee that after a finite number of cycles of circulating tokens all the tokens needed for the request have been collected and it will be granted.

Another form of introducing priorities is to attach them as data attributes to the requests, and involve them in the evaluation of the resource allocation mapping. However, in this case, there is still a possibility that several requests are in conflict. How to decide which of them should be granted? In other words, what sort of parameter should be added to the allocation algorithm in order to guarantee its determinism? The determinism can for example be ensured by having some history parameters stored with the arbiter. For example, in the above situation, we can store the fact that IC1 has been given OC1 k times in a row, and therefore it is not given OC1 again until IC3 has been granted.

Every application suggests a number of alternatives for the topological organization of a distributed arbiter, where ring, mesh and tree (cascaded) structures can be used. The combination of the structure and the resource allocation policy, including both its resource mapping and fairness disciplines, may affect the performance of the arbiter, for example its average response time. There is a trade-off between the average response time and fairness. A tree arbiter with a nearest-neighbour priority [88], for example, optimizes the average response time by passing the resource from a client to its nearest neighbour if the latter is requesting. This happens at the cost of being less fair to more distant neighbours. Another trade-off can be between the response time and energy consumption. For example, a ring-based arbiter, the so called ‘busy ring’, with constantly rotating token (which wastes power if there is no activity in the ring), has a better response than a ring arbiter with a static token, which stays with the most recent owner until requested by another request (and hence saves energy) [89].

While performance, power consumption and fairness are characteristics that can be quantified and traded off against each other, some properties are qualitative. These are mutual exclusion, deadlock-freeness, and liveness. They are general correctness criteria that the design must be verified for. For example, mutual exclusion can be defined for a concurrent system in the following way. Two actions are mutually exclusive if there is no state in which both actions are activated at the same time. A system is deadlock-free if there is no state in which no action is activated. A system is live with respect to an action if from every state the system can reach a state in which this action is activated. These properties can be defined formally using a rigorous notation, such as for example, Petri nets. The system can then be verified against these properties in terms of its Petri net model by various formal tools, such as reachability analysis or checking the unfolding prefix (see, e.g. [90,91]).

This section is organized as follows. We first look at the main handshaking protocols that are used for signalling between arbiters and the clients and resources. This is followed by the introduction of simple two-way arbiters based on synchronizers and MUTEXes. After that we consider more complex arbiters, first looking at the main types of multiway arbiters, built on cascaded (mesh and tree) and linear (ring) architectures. Finally, we look at arbiters with static and dynamic priorities. Here, we effectively treat them as event processors, whose role is not only to perform dynamic conflict resolution in time (saying which event happens first), but also carry out an important computational function associated with the allocation of a resource or resources. Such a separation of concerns is crucial for further development of both the architectural ideas about event processors as well as for the investigation of possible ways to automate their design process.

It should be noted that in this section we only consider arbiters with a single resource. This is not a limitation of our modelling or design approach, it is done mainly to keep the discussion sufficiently simple and concentrate on the aspects of the operation of arbiters from the point of view of its clients. Most of the architectures presented can be relatively easily applied to the case of multiple resources. The reader interested in arbitration problems with multiple resources can refer for example to [92], which describes the so-called Committee Problem. We recommend it as an exercise in applying Petri nets and STGs as a modelling language.

11.4 SIGNAL TRANSITION GRAPHS, OUR MAIN MODELLING LANGUAGE

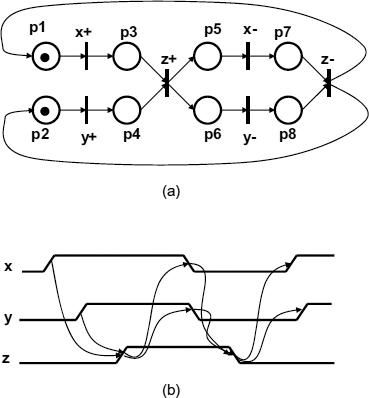
In this section we briefly introduce STGs in order to equip the reader with the basic knowledge of the notation we shall use in this section to describe the behaviour of arbiters. We shall avoid here formal definitions and properties of STGs, as the purpose of using this model is purely illustrative. For a more systematic study of this model, including its use in synthesis and analysis of asynchronous logic with refer the reader to [107] and [108]. Informally, an STG is a Petri net [79] whose transitions are labelled with signal events. Such events are usually changes (i.e. rising and falling edges) of binary signals of the described circuit. An example of the STG which describes the behavior of a two-input Muller C-element is shown in Figure 11.2(a). Figure 11.2(b) represents a timing diagram description of the same behavior.

Figure 11.2 Modeling a Muller C-element: (a) signal transition graph; (b) timing diagram.

Here x and y are input signals, and z is the output of the circuit. The circuit changes its current output value (say, 0), when both its inputs transition from the previous value (0) to the new value (1). A similar synchronization takes place when the circuit's output is originally at logical 1. In the STG in Figure 11.2(a), signal events are labelled in the following way: x+ stands for the rising edge of signal x, and x− denotes the falling edge.

The rules of action of the STGs are the same as those of Petri nets. Every time, all input places (circles in the graph, labelled p1, …, p8) of some transition (a bar in the graph labelled with a particular signal event) contain at least one token (bold dot in the circle) each, the transition is assumed to be enabled and can fire. The firing of an enabled transition results in a change of the net marking (the current assignment of tokens to the places). Exactly one token is removed from each input place of the transition and exactly one token is added to each output place of the transition. The firing action is assumed to be atomic, i.e. it occurs as a single, indivisible event taking no time. An unbounded finite non-negative amount of time can elapse between successive firings (unless the transitions are annotated with delay information, e.g. minimum and maximum intervals, during which the transition can be enabled).

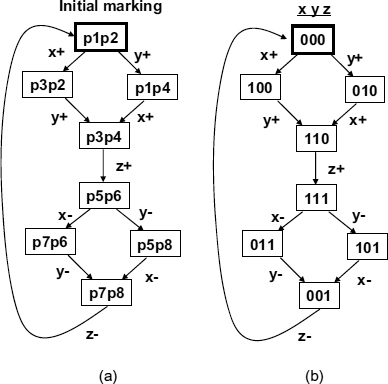
Figure 11.3 State graph for STG of Muller C-element: (a) reachable markings; (b) binary vectors.

The operation of the STG can be traced in the state graph, which is a graph of reachable markings obtained from the potential firings of the enabled transitions. For example, two or more transitions enabled in the same marking can produce alternative sequences of signals changes. If transitions are not sharing input places, like for example transitions x+ and y+ in Figure 11.2(a) (x+ has p1 as its input place, while y+ has p2), their firings can interleave, and form confluent ‘diamond’ structures in the state graph. The state graph for the above STG is shown in Figure 11.3, where part (a) depicts the reachable markings (lists of places marked with tokens), while part (b) shows binary vectors of signal values corresponding to the markings. The latter version is often called the binary encoded state graph of the STG.

For example, the initial marking of the STG (dotted places p1 and p2) corresponds to the top state of the graph. In that marking, all signals have just had a falling transition, so the state can be labelled by the vector 000 (with signal ordering xyz). Two transitions, x+ and y+, are concurrently enabled in that marking. Assuming x+ fires first, its successor (output) place p3 becomes marked, thus reaching the marking p3,p2, whose binary code is 100. Then y+ fires (z+ cannot fire yet, because only one of its input places is marked), thus reaching marking p3,p4, encoded as 110. Now z+ can fire, because both its predecessors are marked, and so on. The complete reachable state graph is constructed by exhaustive firing of the STG transitions, resolving concurrency in all possible ways (e.g. by firing y+ before x+ as well).

The state graph generated by an STG description of a circuit can be used for analysis and verification of the circuit's behaviour in its interaction with the environment. For instance one can state that the system modelled by an STG is free from deadlocks if every reachable state in its corresponding state graph has at least one enabled transition. Other properties can be derived, for example the fact that the model of an arbiter satisfies mutual exclusion can be found by checking if there is a state which can be reached by firing both grants (see Section 11.2). The state graph can also be used to derive the logical implementation of the circuit in the form of the functions of logic gates for all non-input signals. This requires some conditions to be satisfied, namely, that the transitions labelled with the same signal must interleave in the signs (“+” and “−”) for any firing sequence, and that all the states that are labelled with the same vector have the same set of enabled non-input signal transitions. The details of the circuit synthesis method for STGs based on state graphs can be found in [107].

It should be noted that in the STG models we build for arbiters we often use the so-called short-hand STG notation, i.e. we omit places with only one input arc and one output arc, we place the labels of transitions directly, without showing a bar symbol. We will also use signal labels without a sign symbol, say x, to indicate any event on wire x, if we are not interested in the direction of the edge. This will be important for modelling arbiters in two-phase protocols.