1

Synchronization, Arbitration and Choice

1.1 INTRODUCTION

Digital systems have replaced their analog counterparts in computers, signal processing and much of communications hardware at least partly because they are much more reliable. They operate in a domain of absolutes where all the data moving from one place to another is quantized into defined high or low voltages, or binary coded combinations of highs and lows. The great advantage of this is that the data represented by the voltages can be preserved in the presence of small amounts of noise, or variations in component or power supplies, which can affect the voltages. A small variation in a high is still easily distinguished from a low, and a simple circuit, such as a gate or an inverter, can easily restore the correct output level.

In a synchronous system the signal states are also held by flip-flops when the clock ticks. Clocking digitizes time into discrete intervals of time, which are multiples of the clock cycle, with data computed during the first part of the cycle, and guaranteed correct on the next clock rising edge. Small variations in the time taken to evaluate a partial result have no effect on a correctly designed digital system, the data is always correct when it is next clocked. This discipline of two discrete voltage levels and time measured in multiples of the clock period allows most digital components to operate in a controlled environment, provided their outputs do not vary by more than a certain amount from the specified highs and lows, and their output times change only within a narrow band of times, a processor built on the components can be shown to operate correctly.

While this idea has worked well in electronic design for over 50 years the ideal world of a single system of discrete voltage levels and time intervals is not the real world. Within a processor binary data can be moved from one place to another under the control of a single clock, but to be useful the processor must be able to interact with inputs from the outside world, and to send its results back to the real world. Events in the real world are uncertain and unpredictable, the voltage levels from sensors are, at least initially, not the standard high or low voltage, they can occur at any time and can be any voltage level. We can try to hide this problem by using an analog-to-digital converter component which attempts to provide only standard outputs from analog inputs, but this can only ever be partly successful, since it involves a decision when an input is approximately halfway between two possible discrete output representations and one or the other output must be chosen. The mapping of input signal changes to discrete times also presents a problem. When a new input occurs that needs attention from a digital processor, the closed world of the processors discrete voltages and times must be interrupted so that the input can be dealt with. Again, there is a choice, which one out of an integral number of discrete clock cycles should be used to start the processing of that input? Since the input change can occur at any time, there will be occasions when the input is just before the next clock tick, and occasions when it is just after. If it is just before, it gets processed on the next tick, if it is after; it waits until the following tick to be noticed. The problem comes when it happens very close to the clock tick, because then there are two possibilities, this cycle, or the next cycle, and both of them are more or less equally desirable.

1.2 THE PROBLEM OF CHOICE

It looks as if it is easy to make the choices, and it is not a new problem. Whether you can make the choice in an acceptable time, and what it is that determines the choice it something that worried philosophers in the middle ages [1]. One of the first clear statements of the arguments was given by the Arab philosopher Abu Hamid Muhammad Ibn Muhammad al-Tusi al-Shafi'i al-Ghazali who wrote around 1100 AD:

He felt that it was obvious that a man or woman would be able to make the choice, and more specifically, to make the choice before starving to death from lack of food. But in order to decide you have to have some basis for choosing one course of action or another when they appear to be equal in value. His ‘differentiating quality’ was free will, which was thought to be inherent in mankind, but not in animals or machines.

The counter-argument is best given by Jehan Buridan, Rector of Paris University around 1340, in his example of the problem of choice which is usually known as the paradox of Buridan's Ass. In this example a dog is presented with two bowls, or an ass with two bales of hay. It has to choose one of them to eat or else starve to death. Animals were chosen deliberately here because they were not thought to be capable of free will, but even so, he discounts free will as the determining factor writing:

His insight was that the time required for a difficult decision would depend on the evidence available to make it, and if there is insufficient evidence it takes a long time. The implication is that there would be cases when even a man could starve to death because he could not decide.

1.3 CHOICE IN ELECTRONICS

As a philosophical discussion, the problem of choice without preference does not have much impact on real life, but it began to acquire real importance in the 1950s when the first digital computers were designed. For the first time many inputs could be processed in a very short space of time, and each input had first to be synchronized to the processor clock [2].

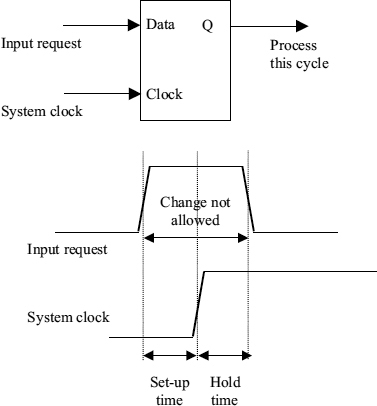
The solution seems obvious, if a digital signal represents the presence of an input, then it may appear at any time, but it can be synchronized to the clock with a simple flip-flop. This circuit is shown in Figure 1.1. When the system clock goes high, the output of the flip-flop will go high if the input was present, and not if it was absent so that the request can be processed in the next clock cycle. The difficulty with this solution is that the input request timing may violate the conditions for which the flip-flop specification is valid. A flip-flop data input must not change after a specified set-up time before the clock rising edge, or before a specified hold time after the clock edge. If it does, any guarantee that the output time will be within the specified times cannot hold.

Figure 1.1 Flip-flop specification.

In fact, as the input change gets closer to the clock edge, the flip-flop takes and longer to respond because the energy supplied by the overlap between data and clock inputs gets less and less, so it takes longer and longer to decide whether or not to interrupt the processor. Eventually, it reaches a level that is just sufficient to bring the Q output of the flip-flop to half way between a high, and a low value. At this point the flip-flop output is exactly balanced between high and low when the clock edge has finished, with no determining factor to push it one way or the other, so it can stay there for a relatively long time. This halfway state is known as a metastable state because it is not stable in the long term, it will eventually go on to be high or fall back to low, but in the metastable state the circuit has no drive towards either the high or low output values. The final outcome may be decided by internal noise, and though a metastable circuit will eventually settle in a well-defined state, the time taken is indeterminate, and could be very long.

If the input time cannot be constrained to change before the set-up time and after the hold time, then the flip-flop output time cannot be constrained either, so all output times relative to the clock also have a finite probability. This can have a knock on effect. If the output can change at any time between one clock edge and the next, it has not been truly synchronized to the clock, and might change part way through a clock cycle. This breaks the rules for a reliable digital system, with the result that systems may fail unpredictably because the processing of the interrupt may not be correct. The probability of a failure in the synchronization process can be very low for an individual interrupt, but because digital processors have to deal with very many inputs per second, the probability of catastrophic failure over a long period of time is not low, and must be at least quantified. It can only be eliminated by removing the need to synchronize, or reduced by allowing more time for the synchronizer to settle. Since there is always a small possibility of a very long settling time we must accept the possibility of failure in systems with a fixed clock period.

This fundamental problem was known to a few people in the early years of computing [2,3], but many, if not most engineers were not aware of the problems presented by synchronizers. In 1973 a special workshop on synchronizer failures was held by Charles Molnar, Director of the Computer Systems Laboratory of Washington University, St Louis to publicize the problem and following this, more people began to accept that computers had been, and were being designed that were unreliable because the designers did not fully understand the problem of metastability. In an article in Scientific American that year a Digital Equipment Corporation engineer is quoted as saying ‘ninety-nine out of a hundred engineers would probably deny the existence of the problem. They believe that conservative design is all you need; you simply allow enough time for a flip-flop to reach a decision. But as computers are designed to run faster and faster the safety factor gets squeezed out… the problem looks irresolvable.’ Even as late as the 1980s a major glitch in the early warning missile radar system was attributed to a poor understanding by designers of the issue of synchronization.

1.4 ARBITRATION

A related problem occurs even if there is no clock. Without a clock, there is no need for synchronization between the input and the clock, but there is a need for arbitration between two competing inputs. Suppose two entirely seperate processors are competing for access to a memory, and only one can be allowed access at a time. The first to request access might get it, and when the memory access is complete, the second is allowed in. But if both make the request within a very short space of time, something must arbitrate between the requests to decide which gets the first access and which the second. As far as the hardware is concerned arbitration is much the same as synchronization, instead of deciding whether the request or the clock tick came first, we are deciding between two (or more) requests. It is only different in the way the arbiter output is treated. If there is no clock in the memory, it does not matter when the arbiter decides which input to accept, provided the data returned by the memory can be processed by the requester at any time. An arbiter can be designed which does not ever fail as a synchronizer might do, because it does not have to make the decision within a clock cycle. As the two requests get closer and closer in time, the arbitration takes longer and longer, and since the requests can occur within an infinitesmally small time, the response can take an infinitely long time. Instead of a failure rate there is a small probability of very long times, which may matter just as much in a real-time application as small probability of failure. Does it matter if a plane flies into a mountain because the navigation system fails, or it flies into the mountain because it cannot decide in time which way to go around?

1.5 CONTINUOUS AND DISCRETE QUANTITIES

Are we stuck with computer systems that may fail, or may not provide answers in the time we need them, or is there some circuit solution that will solve the problem? Unfortunately the basic problem has little to do with circuits. It is that real world inputs are continuous in both voltage and time. A continuous voltage input can have any value between the maximum and the minimum voltage level, say between 0 and 1 V, and there are an infinite number of possible values, 0.1, 0.2, 0.5 V, etc. between those two limits. On the other hand there are only two possible voltages for a binary coded signal, which might be 0 or 1 V. To decide which we must make a comparison between a fixed value, maybe 0.5 V, and the input. If the input is less than 0.5 V the output is 1, and if it is greater than 0.5 V the output is zero. It is possible to choose a voltage of 0.49 V as an input. This will be only 0.01 V different from the comparison value, so the comparison circuit has only a small voltage to work on. Any real physical circuit takes some time to produce an output of 1 V, and the smaller the input, the longer it takes. With a 0.4999 V input the circuit has an input of only 0.0001 V to work on, so it takes much longer to make the comparison, and in general there is no limit to the time that might be required for the comparison, because the input to the comparator circuit can be infinitesimally small.

Similarly, the processor interrupt can occur at an infinite number of instants between one clock edge and the next, and comparisons may have to be made on an infinitesimally small time interval. Again that could mean an infinite response time, and there will be a resulting probability of failure. To compute the failure rate you only need to decide the maximum time that the synchronizer has available to make its comparison, and then estimate how often the comparator input is small enough to cause the output to exceed that maximum.

1.6 TIMING

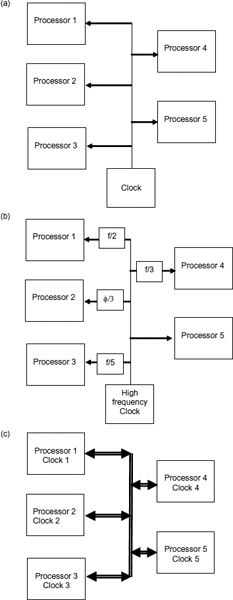
Synchronization of data passing between two systems is only necessary if the timing of the systems is different. If both systems work to the same clock, then they are synchronous and changes in the data from one system are always made at the same time in its clock cycle. The receiving system knows when the data is stable relative to its own clock and can sample it at that time so no synchronization is necessary. There are many possible clocking schemes for systems on a chip and Figure 1.2 shows three of them. In (a) a single clock is fed to all the processors, so that the whole system is essentially synchronous.

If the two clocks are not the same but linked, maybe through a phase locked loop, the relative timing might vary a little, but is essentially stable. Provided this phase variation is limited, it is still possible to transfer data at mutually compatible times without the need to use a synchronizer. The relationship is known as mesochronous. In (b), the individual processor clocks are all linked to the same source so that the timing is still synchronous or mesochronous. Often it is not possible to link the clocks of the sending and receiving system as they may be some distance apart. This is the situation in (c). Both clock frequencies may be nominally the same, but the phase difference can drift over a period of time in an unbounded manner. This relationship is called plesiochronous and there are times when both clocks are in phase and times where they are not. These points are to some extent predictable in advance, so synchronization can be achieved by predicting when conflicts might occur, and avoiding data transfers when the two clocks conflict. If the time frame of one system is completely unknown to the other, there is no way that a conflict can be avoided and it is essential that data transfers are synchronized every time. In this case the path is heterochronous. Heterochronous, plesiochronous and mesochronous are all examples of asynchronous timing.

Figure 1.2 Clocking schemes: (a) single clock, multiple domains; (b) rational clock frequencies; (c) multiple clocks.

1.7 BOOK STRUCTURE

The rest of this book has three main Parts. Part I is concerned with basic models of metastability in circuits, Part II with synchronization in systems, and Part III with arbitration.

In Part I, Chapters 2-5, mathematical models for metastability are derived which can be applied to simple synchronizer circuits with a view to explaining how the failure rates vary in different conditions. Having established the mathematical tools for comparing different circuits we present the key circuits used for synchronization and arbitration, the mutual exclusion element (MUTEX), the synchronizer Jamb latch, and the Q-flop. Modifications of these basic circuits to achieve higher performance and arbitration between more than two inputs are also described. Chapter 4 shows how thermal and other noise effects affect metastability, and the basic assumptions that must be satisfied in a system to allow the simple MTBF formulas to be used. Chapter 5 describes how metastability and synchronizer reliability can be measured. The metastability T_w and resolution time constant τ are defined and then methods for plotting typical histograms of failures against output time. From this we derive mean time between synchronizer failure in a system against synchronizer time, and input time against output time. Test methods suitable for on and off chip synchronizer measurement, both for custom ICs and field programmable devices, are discussed together with appropriate time measuring circuits. System reliability is dependent on metastable events occurring very late in the clock cycle, where the final state is determined by noise, or ‘deep metastability’. Methods for measuring effects in this region including the effect of the back edge of the clock are explained.

In Part II, Chapters 6 and 7 discuss how synchronizers fit into a digital system. In Chapter 6, a system level view of synchronizers in presented. Where synchronization occurs in a multiply clocked system, how it can be avoided, and where it cannot be avoided, how to mitigate the effects of latency due to synchronizer resolution time are discussed. High-throughput, low-latency, and speculative systems are described in Chapter 7, with the trade-offs between these two aspects of design. An alternative to multiple independent clocks is to use stoppable or pausible clocks. How these fit into a GALS system shown in Chapter 8. Chapter 9 concludes this Part.

Chapters 10–14 (Part III) present ideas about designing complex asynchronous arbiters using the building blocks studied in the previous chapters, such as synchronizers and mutual exclusion elements. These arbiters are built as speed-independent circuits, a class of circuits that guarantees their robust operation regardless of gate delays and any delay in handshake interconnects with the environment. A general definition for an arbiter is given and then a range of arbiters is covered, from simple two-way arbiters to tree-based and ring-based arbiters, finishing with a detailed examination of various types of priority arbiters, including static and dynamic priority schemes. The behaviour of arbiters is described throughout by Petri nets and their special interpretation signal transition graphs. The latter replace sets of traditional timing diagrams and provide a compact and formal specification of nontrivial dynamic behaviour of arbiters, potentially amenable to formal verification by existing Petri net analysis tools. The presented models and circuits enable solving complex arbitration problems encountered in a wide range of applications such as system-on-chip buses, network-on-chip and asynchronous distributed system in a more general sense.