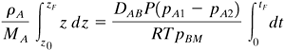6.2. MOLECULAR DIFFUSION IN GASES

6.2A. Equimolar Counterdiffusion in Gases

In Fig. 6.2-1 a diagram is given of two gases A and B at constant total pressure P in two large chambers connected by a tube where molecular diffusion at steady state is occurring. Stirring in each chamber keeps the concentrations in each chamber uniform. The partial pressure p_A1 > p_A2 and p_B2 > p_B1. Molecules of A diffuse to the right and B to the left. Since the total pressure P is constant throughout, the net moles of A diffusing to the right must equal the net moles of B to the left. If this is not so, the total pressure would not remain constant. This means that

Equation 6.2-1

The subscript z is often dropped when the direction is obvious. Writing Fick's law for B for constant c,

Equation 6.2-2

Now since P = p_A + p_B = constant, then

Equation 6.2-3

Differentiating both sides,

Equation 6.2-4

Equating Eq. (6.1-3) to (6.2-2),

Equation 6.2-5

Substituting Eq. (6.2-4) into (6.2-5) and canceling like terms,

Equation 6.2-6

This shows that for a binary gas mixture of A and B, the diffusivity coefficient D_AB for A diffusing into B is the same as D_BA for B diffusing into A.

EXAMPLE 6.2-1. Equimolar Counterdiffusion Ammonia gas (A) is diffusing through a uniform tube 0.10 m long containing N2 gas (B) at 1.0132 × 105 Pa pressure and 298 K. The diagram is similar to Fig. 6.2-1. At point 1, pA1 = 1.013 × 104 Pa and at point 2, pA2 = 0.507 × 104 Pa. The diffusivity DAB = 0.230 × 10−4 m2/s. Calculate the flux at steady state. Repeat for Solution: Equation (6.1-13) can be used, where P = 1.0132 × 105 Pa, z2 − z1 = 0.10 m, and T = 298 K. Substituting into Eq. (6.1-13) for part (a), Rewriting Eq. (6.1-13) for component B for part (b) and noting that pB1 = P − pA1 = 1.0132 × 105 − 1.013 × 104 = 9.119 × 104 Pa and pB2 = P − pA2 = 1.0132 × 105 − 0.507 × 104 = 9.625 × 104 Pa, The negative value for means the flux goes from point 2 to point 1.

6.2B. General Case for Diffusion of Gases A and B Plus Convection

Up to now we have considered Fick's law for diffusion in a stationary fluid; that is, there has been no net movement or convective flow of the entire phase of the binary mixture A and B. The diffusion flux occurred because of the concentration gradient. The rate at which moles of A passed a fixed point to the right, which will be taken as a positive flux, is kg mol A/s · m². This flux can be converted to a velocity of diffusion of A to the right by

Equation 6.2-7

where ν_Ad is the diffusion velocity of A in m/s.

Now let us consider what happens when the whole fluid is moving in bulk or convective flow to the right. The molar average velocity of the whole fluid relative to a stationary point is ν_M m/s. Component A is still diffusing to the right, but now its diffusion velocity ν_Ad is measured relative to the moving fluid. To a stationary observer A is moving faster than the bulk of the phase, since its diffusion velocity ν_Ad is added to that of the bulk phase ν_M. Expressed mathematically, the velocity of A relative to the stationary point is the sum of the diffusion velocity and the average or convective velocity:

Equation 6.2-8

where ν_A is the velocity of A relative to a stationary point. Expressed pictorially,

Multiplying Eq. (6.2-8) by c_A,

Equation 6.2-9

Each of the three terms represents a flux. The first term, c_Aν_A, can be represented by the flux N_A kg mol A/s · m². This is the total flux of A relative to the stationary point. The second term is , the diffusion flux relative to the moving fluid. The third term is the convective flux of A relative to the stationary point. Hence, Eq. (6.2-9) becomes

Equation 6.2-10

Let N be the total convective flux of the whole stream relative to the stationary point. Then,

Equation 6.2-11

Or, solving for v_M,

Equation 6.2-12

Substituting Eq. (6.2-12) into (6.2-10),

Equation 6.2-13

Since is Fick's law, Eq. (6.1-7),

Equation 6.2-14

Equation (6.2-14) is the final general equation for diffusion plus convection to use when the flux N_A is used, which is relative to a stationary point. A similar equation can be written for N_B.

Equation 6.2-15

To solve Eq. (6.2-14) or (6.2-15), the relation between the flux N_A and N_B must be known. Equations (6.2-14) and (6.2-15) hold for diffusion in a gas, liquid, or solid.

For equimolar counterdiffusion, N_A = −N_B and the convective term in Eq. (6.2-14) becomes zero. Then, N_A = = −N_B =×.

6.2C. Special Case for A Diffusing Through Stagnant, Nondiffusing B

The case of diffusion of A through stagnant or nondiffusing B at steady state often occurs. In this case one boundary at the end of the diffusion path is impermeable to component B, so it cannot pass through. One example, shown in Fig. 6.2-2a, is in the evaporation of a pure liquid such as benzene (A) at the bottom of a narrow tube, where a large amount of inert or nondiffusing air (B) is passed over the top. The benzene vapor (A) diffuses through the air (B) in the tube. The boundary at the liquid surface at point 1 is impermeable to air, since air is insoluble in benzene liquid. Hence, air (B) cannot diffuse into or away from the surface. At point 2 the partial pressure p_A2 = 0, since a large volume of air is passing by.

Another example, shown in Fig. 6.2-2b, occurs in the absorption of NH₃ (A) vapor which is in air (B) by water. The water surface is impermeable to the air, since air is only very slightly soluble in water. Thus, since B cannot diffuse, N_B = 0.

To derive the case for A diffusing in stagnant, nondiffusing B, N_B = 0 is substituted into the general Eq. (6.2-14):

Equation 6.2-16

The convective flux of A is (c_A/c)(N_A + 0). Keeping the total pressure P constant, substituting c = P/RT, p_A = x_AP, and c_A/c = p_A/P into Eq. (6.2-16),

Equation 6.2-17

Rearranging and integrating,

Equation 6.2-18

Equation 6.2-19

Equation 6.2-20

Equation (6.2-20) is the final equation to be used to calculate the flux of A. However, it is often written in another form. A log mean value of the inert B is defined as follows. Since P = p_A1 + p_B1 = p_A2 + p_B2, p_B1 = P − p_A1, and p_B2 = P − p_A2,

Equation 6.2-21

Substituting Eq. (6.2-21) into (6.2-20),

Equation 6.2-22

EXAMPLE 6.2-2. Diffusion of Water Through Stagnant, Nondiffusing Air Water in the bottom of a narrow metal tube is held at a constant temperature of 293 K. The total pressure of air (assumed dry) is 1.01325 × 105 Pa (1.0 atm) and the temperature is 293 K (20°C). Water evaporates and diffuses through the air in the tube, and the diffusion path z2 − z1 is 0.1524 m (0.5 ft) long. The diagram is similar to Fig. 6.2-2a. Calculate the rate of evaporation at steady state in lb mol/h · ft2 and kg mol/s · m2. The diffusivity of water vapor at 293 K and 1 atm pressure is 0.250 × 10−4 m2/s. Assume that the system is isothermal. Use SI and English units. Solution: The diffusivity is converted to ft2/h by using the conversion factor from Appendix A.1: From Appendix A.2 the vapor pressure of water at 20°C is 17.54 mm, or pA1 = 17.54/760 = 0.0231 atm = 0.0231(1.01325 × 105) = 2.341 × 103 Pa, pA2 = 0 (pure air). Since the temperature is 20°C (68°F), T = 460 + 68 = 528°R = 293 K. From Appendix A.1, R = 0.730 ft3 · atm/lb · mol·°R. To calculate the value of pBM from Eq. (6.2-21), Since pB1 is close to pB2, the linear mean (pB1 + pB2)/2 could be used and would be very close to pBM. Substituting into Eq. (6.2-22) with z2 − z1 = 0.5 ft (0.1524 m),

EXAMPLE 6.2-3. Diffusion in a Tube with Change in Path Length Diffusion of water vapor in a narrow tube is occurring as in Example 6.2-2 under the same conditions. However, as shown in Fig. 6.2-2a, at a given time t, the level is z m from the top. As diffusion proceeds, the level drops slowly. Derive the equation for the time tF for the level to drop from a starting point of z0 m at t = 0 to zF at t = tF s as shown. Solution: We assume a pseudo-steady-state condition since the level drops very slowly. As time progresses, the path length z increases. At any time t, Eq. (6.2-22) holds; but the path length is z and Eq. (6.2-22) becomes as follows, where NA and z are now variables: Equation 6.2-23 Assuming a cross-sectional area of 1 m2, the level drops dz m in dt s, and ρA(dz · 1)/MA is the kg mol of A that have left and diffused. Then, Equation 6.2-24 Equating Eq. (6.2-24) to (6.2-23), rearranging, and integrating between the limits of z = z0 when t = 0 and z = zF when t = tF, Equation 6.2-25 Solving for tF, Equation 6.2-26

The method shown in Example 6.2-3 has been used to experimentally determine the diffusivity D_AB. In this experiment the starting path length z₀ is measured at t = 0 together with the final z_F at t_F. Then Eq. (6.2-26) is used to calculate D_AB.

6.2D. Diffusion Through a Varying Cross-Sectional Area

So far, in the cases at steady state we have considered N_A and as constants in the integrations. In these cases the cross-sectional area A m² through which the diffusion occurs has been constant with varying distance z. In some situations the area A may vary. Then it is convenient to define N_A as

Equation 6.2-27

where is kg moles of A diffusing per second or kg mol/s. At steady state, will be constant but not A for a varying area.

1. Diffusion from a sphere

To illustrate the use of Eq. (6.2-27), the important case of diffusion to or from a sphere in a gas will be considered. This situation appears often, in such cases as the evaporation of a drop of liquid, the evaporation of a ball of naphthalene, and the diffusion of nutrients to a sphere-like microorganism in a liquid. In Fig. 6.2-3a is shown a sphere of fixed radius r₁ m in an infinite gas medium. Component (A) at partial pressure p_A1 at the surface is diffusing into the surrounding stagnant medium (B), where p_A2 = 0 at some large distance away. Steady-state diffusion will be assumed.

The flux N_A can be represented by Eq. (6.2-27), where A is the cross-sectional area 4πr² at point r distance from the center of the sphere. Also, is a constant at steady state:

Equation 6.2-28

Since this is a case of A diffusing through stagnant, nondiffusing B, Eq. (6.2-18) will be used in its differential form and N_A will be equated to Eq. (6.2-28), giving

Equation 6.2-29

Note that dr was substituted for dz. Rearranging and integrating between r₁ and some point r₂ a large distance away,

Equation 6.2-30

Equation 6.2-31

Since , 1/r₂ ≅ 0. Substituting p_BM from Eq. (6.2-21) into Eq. (6.2-31),

Equation 6.2-32

This equation can be simplified further. If p_A1 is small compared to P (a dilute gas phase),P_BM ≅ P . Also, setting 2r₁ = D₁, diameter, and c_A1 = p_A1/RT, we obtain

Equation 6.2-33

This equation can also be used for liquids, where D_AB is the diffusivity of A in the liquid.

EXAMPLE 6.2-4. Evaporation of a Naphthalene Sphere A sphere of naphthalene having a radius of 2.0 mm is suspended in a large volume of still air at 318 K and 1.01325 × 105 Pa (1 atm). The surface temperature of the naphthalene can be assumed to be at 318 K and its vapor pressure at 318 K is 0.555 mm Hg. The DAB of naphthalene in air at 318 K is 6.92 × 10−6 m2/s. Calculate the rate of evaporation of naphthalene from the surface. Solution: The flow diagram is similar to Fig. 6.2-3a. DAB = 6.92 × 10−6 m2/s, pA1 = (0.555/760)(1.01325 × 105) = 74.0 Pa, pA2 = 0, r1 = 2/1000 m, R = 8314 m3· Pa/kg mol · K, pB1 = P − pA1 = 1.01325 × 105 − 74.0 = 1.01251 × 105 Pa, pB2 = P − pA2 = 1.01325 × 105 − 0. Since the values of pB1 and pB2 are close to each other, Substituting into Eq. (6.2-32),

If the sphere in Fig. 6.2-3a is evaporating, the radius r of the sphere decreases slowly with time. The equation for the time it takes for the sphere to evaporate completely can be derived by assuming pseudo-steady state and by equating the diffusion flux equation (6.2-32), where r is now a variable, to the moles of solid A evaporated per dt time and per unit area as calculated from a material balance. (See Problem 6.2-9 for this case.) The material-balance method is similar to Example 6.2-3. The final equation is

Equation 6.2-34

where r₁ is the original sphere radius, ρ_A the density of the sphere, and M_A the molecular weight.

2. Diffusion through a conduit of nonuniform cross-sectional area

In Fig. 6.2-3b component A is diffusion at steady state through a circular conduit which is tapered uniformally as shown. At point 1 the radius is r₁ and at point 2 it is r₂. At position z in the conduit, for A diffusing through stagnant, nondiffusing B,

Equation 6.2-35

Using the geometry shown, the variable radius r can be related to position z in the path as follows:

Equation 6.2-36

This value of r is then substituted into Eq. (6.2-35) to eliminate r and the equation integrated:

Equation 6.2-37

A case similar to this is given in Problem 6.2-10.

6.2E. Diffusion Coefficients for Gases

1. Experimental determination of diffusion coefficients

A number of different experimental methods have been used to determine the molecular diffusivity for binary gas mixtures. Several of the important methods are as follows. One method is to evaporate a pure liquid in a narrow tube with a gas passed over the top, as shown in Fig. 6.2-2a. The fall in liquid level is measured with time and the diffusivity calculated from Eq. (6.2-26).

In another method, two pure gases having equal pressures are placed in separate sections of a long tube separated by a partition. The partition is slowly removed and diffusion proceeds. After a given time the partition is reinserted and the gas in each section analyzed. The diffusivities of the vapor of solids such as naphthalene, iodine, and benzoic acid in a gas have been obtained by measuring the rate of evaporation of a sphere. Equation (6.2-32) can be used. See Problem 6.2-9 for an example of this.

A method often used is the two-bulb method (N1). The apparatus consists of two glass bulbs with volumes V₁ and V₂ m³ connected by a capillary of cross-sectional area A m² and length L whose volume is small compared to V₁ and V₂, as shown in Fig. 6.2-4. Pure gas A is added to V₁ and pure B to V₂ at the same pressures. The valve is opened, diffusion proceeds for a given time, and then the valve is closed and the mixed contents of each chamber are sampled separately.

The equations can be derived by neglecting the capillary volume and assuming each bulb is always of a uniform concentration. Assuming quasi-steady-state diffusion in the capillary,

Equation 6.2-38

where c₂ is the concentration of A in V₂ at time t and c₁ in V₁. The rate of diffusion of A going to V₂ is equal to the rate of accumulation in V₂:

Equation 6.2-39

The average value c_av at equilibrium can be calculated by a material balance from the starting compositions and at t = 0:

Equation 6.2-40

A similar balance at time t gives

Equation 6.2-41

Substituting c₁ from Eq. (6.2-41) into (6.2-39), rearranging, and integrating between t = 0 and t = t, the final equation is

Equation 6.2-42

If c₂ is obtained by sampling at t, D_AB can be calculated.

2. Experimental diffusivity data

Some typical data are given in Table 6.2-1. Other data are tabulated in Perry and Green (P1) and Reid et al. (R1). The values range from about 0.05 × 10⁻⁴ m²/s, where a large molecule is present, to about 1.0 × 10⁻⁴ m²/s, where H₂ is present at room temperatures. The relation between diffusivity in m²/s and ft²/h is 1 m²/s = 3.875 × 10⁴ ft²/h.

Table 6.2-1. Diffusion Coefficients of Gases at 101.32 kPa Pressure

System	Temperature		Diffusivity [(m2/s)104 or cm2/s]	Ref.
	°C	K
Air–NH3	0	273	0.198	(W1)
Air–H2O	0	273	0.220	(N2)
	25	298	0.260	(L1)
	42	315	0.288	(M1)
Air–CO2	3	276	0.142	(H1)
	44	317	0.177
Air–H2	0	273	0.611	(N2)
Air–C2H5OH	25	298	0.135	(M1)
	42	315	0.145
Air–CH3COOH	0	273	0.106	(N2)
Air–n-hexane	21	294	0.080	(C1)
Air–benzene	25	298	0.0962	(L1)
Air–toluene	25.9	298.9	0.086	(G1)
Air–n-butanol	0	273	0.0703	(N2)
	25.9	298.9	0.087
H2–CH4	25	298	0.726	(C2)
H2–N2	25	298	0.784	(B1)
	85	358	1.052
H2–benzene	38.1	311.1	0.404	(H2)
H2–Ar	22.4	295.4	0.83	(W2)
H2–NH3	25	298	0.783	(B1)
H2–SO2	50	323	0.61	(S1)
H2–C2H5OH	67	340	0.586	(T1)
He–Ar	25	298	0.729	(S2)
He–n-butanol	150	423	0.587	(S2)
He–air	44	317	0.765	(H1)
He–CH4	25	298	0.675	(C2)
He–N2	25	298	0.687	(S2)
He–O2	25	298	0.729	(S2)
Ar–CH4	25	298	0.202	(C2)
CO2–N2	25	298	0.167	(W3)
CO2–O2	20	293	0.153	(W4)
N2–n-butane	25	298	0.0960	(B2)
H2O–CO2	34.3	307.3	0.202	(S3)
CO–N2	100	373	0.318	(A1)
CH3Cl–SO2	30	303	0.0693	(C3)
(C2H5)2O–NH3	26.5	299.5	0.1078	(S4)

3. Prediction of diffusivity for gases

The diffusivity of a binary gas mixture in the dilute gas region, that is, at low pressures near atmospheric, can be predicted using the kinetic theory of gases. The gas is assumed to consist of rigid spherical particles that are completely elastic on collision with another molecule, which implies that momentum is conserved.

In a simplified treatment it is assumed that there are no attractive or repulsive forces between the molecules. The derivation uses the mean free path λ, which is the average distance that a molecule has traveled between collisions. The final equation is

Equation 6.2-43

where ū is the average velocity of the molecules. The final equation obtained after substituting expressions for ū and λ into Eq. (6.2-43) is approximately correct, since it correctly predicts D_AB proportional to 1/pressure and approximately predicts the temperature effect.

A more accurate and rigorous treatment must consider the intermolecular forces of attraction and repulsion between molecules as well as the different sizes of molecules A and B. Chapman and Enskog (H3) solved the Boltzmann equation, which uses a distribution function instead of the mean free path λ. To solve the equation, a relation between the attractive and repulsive forces between a given pair of molecules must be used. For a pair of nonpolar molecules, a reasonable approximation to the forces is the Lennard–Jones function.

The final relation for predicting the diffusivity of a binary gas pair of A and B molecules is

Equation 6.2-44

where D_AB is the diffusivity in m²/s, T temperature in K, M_A molecular weight of A in kg mass/kg mol, M_B molecular weight of B, and P absolute pressure in atm. The term σ_AB is an “average collision diameter” and Ω_D,AB is a collision integral based on the Lennard–Jones potential. Values of σ_A and σ_B as well as Ω_D,AB can be obtained from a number of sources (B3, G2, H3, R1).

The collision integral Ω_D,AB is a ratio giving the deviation of a gas with interactions as compared to a gas of rigid, elastic spheres. This value would be 1.0 for a gas with no interactions. Equation (6.2-44) predicts diffusivities with an average deviation of about 8% up to about 1000 K (R1). For a polar–nonpolar gas mixture, Eq. (6.2-44) can be used if the correct force constant is used for the polar gas (M1, M2). For polar–polar gas pairs, the potential-energy function commonly used is the Stockmayer potential (M2).

The effect of concentration of A in B in Eq. (6.2-44) is not included. However, for real gases with interactions, the maximum effect of concentration on diffusivity is about 4% (G2). In most cases the effect is considerably less, and hence it is usually neglected.

Equation (6.2-44) is relatively complicated to use, and often some of the constants such as σ_AB are not available or are difficult to estimate. Hence, the semiempirical method of Fuller et al. (F1), which is much more convenient to use is often preferred. The equation was obtained by correlating many recent data and uses atomic volumes from Table 6.2-2, which are summed for each gas molecule. The equation is

Equation 6.2-45

Table 6.2-2. Atomic Diffusion Volumes for Use with the Fuller, Schettler, and Giddings Method^[*]

Atomic and structural diffusion volume increments, v
C	16.5	(C1)	19.5
H	1.98	(S)	17.0
O	5.48	Aromatic ring	−20.2
(N)	5.69	Heterocyclic ring	−20.2
Diffusion volumes for simple molecules, Ε v
H2	7.07	CO	18.9
D2	6.70	CO2	26.9
He	2.88	N2O	35.9
N2	17.9	NH3	14.9
O2	16.6	H2O	12.7
Air	20.1	(CCl2F2)	114.8
Ar	16.1	(SF6)	69.7
Kr	22.8	(Cl2)	37.7
(Xe)	37.9	(Br2)	67.2
Ne	5.59	(SO2)	41.1
Source: Reprinted with permission from E. N. Fuller, P. D. Schettler, and J. C. Giddings, Ind. Eng. Chem., 58, 19(1966). Copyright by the American Chemical Society.

^[*] Parentheses indicate that the value listed is based on only a few data points.

where Ε v_A = sum of structural volume increments, Table 6.2-2, and D_AB = m²/s. This method can be used for mixtures of nonpolar gases or for a polar–nonpolar mixture. Its accuracy is not quite as good as that of Eq. (6.2-44).

The equation shows that D_AB is proportional to 1/P and to T^1.75. If an experimental value of D_AB is available at a given T and P and it is desired to have a value of D_AB at another T and P, one should correct the experimental value to the new T and P by means of the relationship D_AB ∝ T^1.75/P.

4. Schmidt number of gases

The Schmidt number of a gas mixture of dilute A in B is dimensionless and is defined as

Equation 6.2-46

where µ is viscosity of the gas mixture, which is viscosity of B for a dilute mixture in Pa · s or kg/m · s, D_AB is diffusivity in m²/s, and ρ is the density of the mixture in kg/m³. For a gas the Schmidt number can be assumed independent of temperature over moderate ranges and independent of pressure up to about 10 atm or 10 × 10⁵ Pa.

The Schmidt number is the dimensionless ratio of the molecular momentum diffusivity μ/ρ to the molecular mass diffusivity D_AB. Values of the Schmidt number for gases range from about 0.5 to 2. For liquids Schmidt numbers range from about 100 to over 10 000 for viscous liquids.

EXAMPLE 6.2-5. Estimation of Diffusivity of a Gas Mixture Normal butanol (A) is diffusing through air (B) at 1 atm abs. Using the Fuller et al. method, estimate the diffusivity DAB for the following temperatures and compare with the experimental data: For 0°C. For 25.9°C. For 0°C and 2.0 atm abs. Solution: For part (a), P = 1.00 atm, T = 273 + 0 = 273 K, MA (butanol) = 74.1, MB (air) = 29. From Table 6.2-2, Substituting into Eq. (6.2-45), This value deviates by +10% from the experimental value of 7.03 × 10−6 m2/s from Table 6.2-1. For part (b), T = 273 + 25.9 = 298.9. Substituting into Eq. (6.2-45), DAB = 9.05 × 10−6 m2/s. This value deviates by +4% from the experimental value of 8.70 × 10−6 m2/s. For part (c), the total pressure P = 2.0 atm. Using the value predicted in part (a) and correcting for pressure,