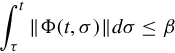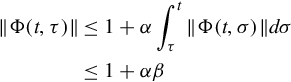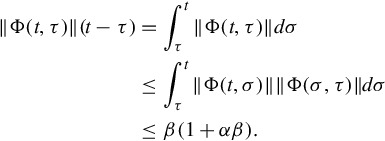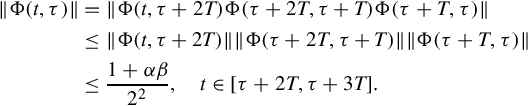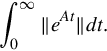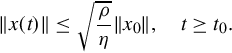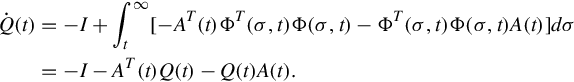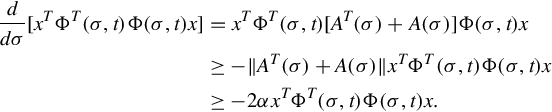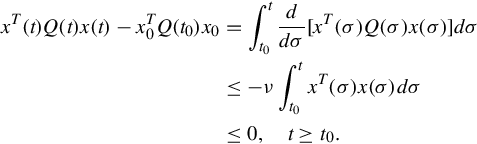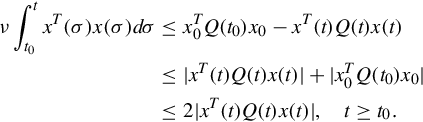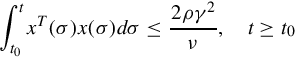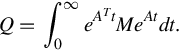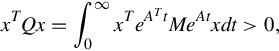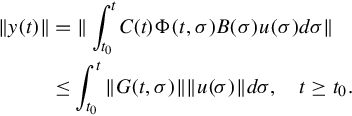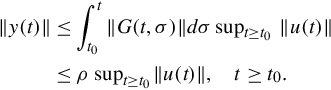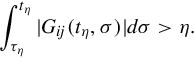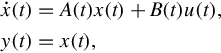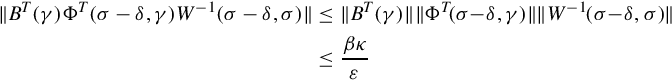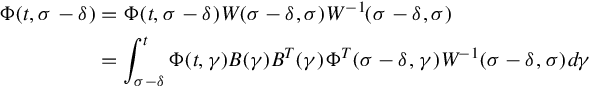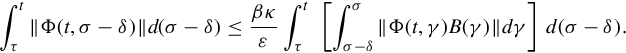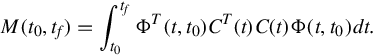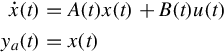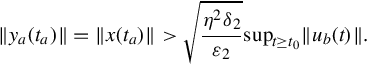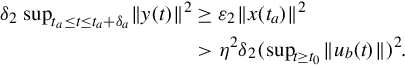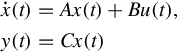5.1.1 Uniform exponential stability

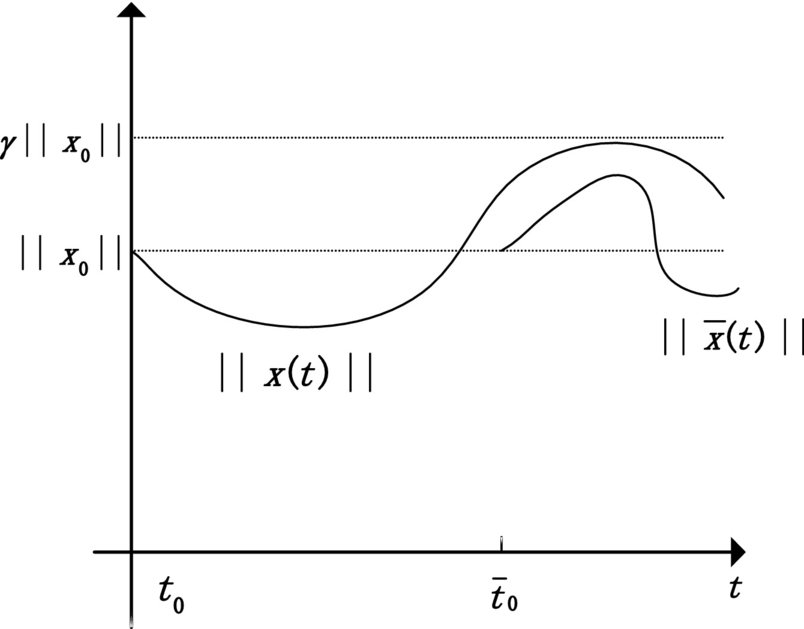
Next we consider a stability property for Eq. (5.1) that addresses both boundedness and asymptotic behavior of solution. It implies uniform stability, and imposes an additional requirement that all solutions approach zero exponentially as $t\to \infty$.

Again γ is no less than unity, and the adjective uniform refers to the fact that γ and λ are independent of t₀. This is illustrated in Fig. 5.2. The property of uniform exponential stability can be expressed in terms of an exponential bound on the transition matrix. The proof is similar to that of Theorem 5.1.1.

Uniform stability and uniform exponential stability are the only internal stability concepts used in the sequel. Uniform exponential stability is the most important of the two, and another theoretical characterization of uniform exponentially stability for the bounded-coefficient case will prove useful.

Conversely suppose Eq. (5.7) holds. Basic calculus permit the representation

$\begin{array}{l}\hfill \begin{array}{cc}\mathrm{\Phi }(t,\tau )& =I-{\int }_{\tau }^t\frac{\partial }{\partial \sigma }\mathrm{\Phi }(t,\sigma )d\sigma \\ & =I+{\int }_{\tau }^t\mathrm{\Phi }(t,\sigma )A(\sigma )d\sigma \end{array}\end{array}$

and thus

$\begin{array}{l}\hfill \begin{array}{cc}\parallel \mathrm{\Phi }(t,\tau )\parallel & \le 1+\alpha {\int }_{\tau }^t\parallel \mathrm{\Phi }(t,\sigma )\parallel d\sigma \\ & \le 1+\alpha \beta \end{array}\end{array}$

for all t, τ such that t ≥ τ. In completing this proof the composition property of the transition matrix is crucial. So long as t ≥ τ we can write, cleverly,

$\begin{array}{l}\hfill \begin{array}{cc}\parallel \mathrm{\Phi }(t,\tau )\parallel (t-\tau )& ={\int }_{\tau }^t\parallel \mathrm{\Phi }(t,\tau )\parallel d\sigma \\ & \le {\int }_{\tau }^t\parallel \mathrm{\Phi }(t,\sigma )\parallel \parallel \mathrm{\Phi }(\sigma ,\tau )\parallel d\sigma \\ & \le \beta (1+\alpha \beta ).\end{array}\end{array}$

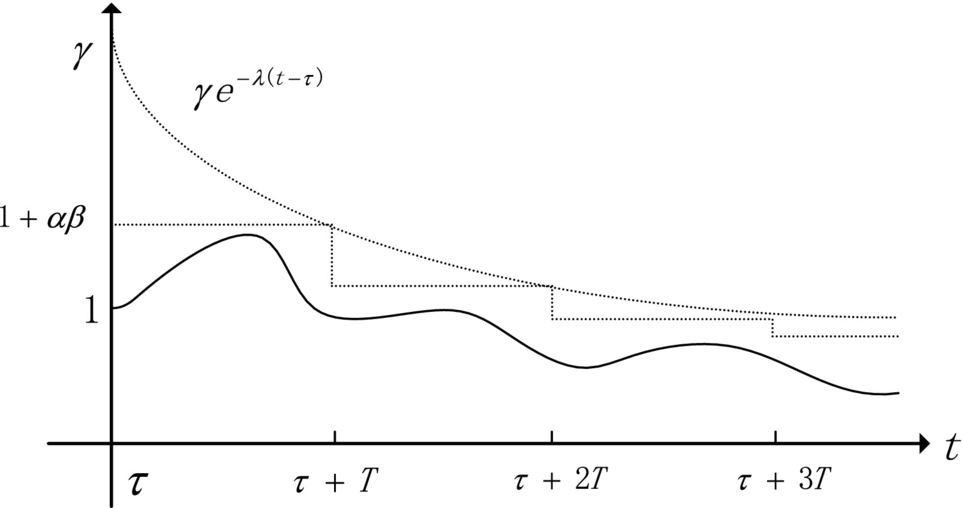
Therefore letting T = 2β(1 + αβ) and t = τ + T gives

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(\tau +T,\tau )\parallel \le \frac{1}{2}\end{array}$

for all τ. Applying Eqs. (5.8), (5.9), the following inequalities on time intervals of the form [τ + κT, τ + (κ + 1)T), where τ is arbitrary, are transparent:

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t,\tau )\parallel \le 1+\alpha \beta ,t\in [\tau ,\tau +T]\end{array}$

$\begin{array}{l}\hfill \begin{array}{cc}\parallel \mathrm{\Phi }(t,\tau )\parallel & =\parallel \mathrm{\Phi }(t,\tau +T)\mathrm{\Phi }(\tau +T,\tau )\parallel \\ & \le \parallel \mathrm{\Phi }(t,\tau +T)\parallel \parallel \mathrm{\Phi }(\tau +T,\tau )\parallel \\ & \le \frac{1+\alpha \beta }{2},t\in [\tau +T,\tau +2T],\end{array}\end{array}$

$\begin{array}{l}\hfill \begin{array}{cc}\parallel \mathrm{\Phi }(t,\tau )\parallel & =\parallel \mathrm{\Phi }(t,\tau +2T)\mathrm{\Phi }(\tau +2T,\tau +T)\mathrm{\Phi }(\tau +T,\tau )\parallel \\ & \le \parallel \mathrm{\Phi }(t,\tau +2T)\parallel \parallel \mathrm{\Phi }(\tau +2T,\tau +T)\parallel \parallel \mathrm{\Phi }(\tau +T,\tau )\parallel \\ & \le \frac{1+\alpha \beta }{2^2},t\in [\tau +2T,\tau +3T].\end{array}\end{array}$

Continuing in this fashion shows that for any value of τ

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t,\tau )\parallel \le \frac{1+\alpha \beta }{2^k},t\in [\tau +kT,\tau +(k+1)T].\end{array}$

Finally, choose $\lambda =(-\frac{1}{T})ln\left(\frac{1}{2}\right)$ and γ = 2(1 + αβ). Fig. 5.3 presents a plot of the corresponding decaying exponential and the bound (5.10), from which it is clear that

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t,\tau )\parallel \le \gamma e^{-\lambda (t-\tau )}\end{array}$

for all t, τ such that t ≥ τ. Uniform exponential stability thus is a consequence of Theorem 5.1.1.

An alternate form for the uniform exponential stability condition in Theorem 5.1.3 is

$\begin{array}{l}\hfill {\int }_{-\infty }^t\parallel \mathrm{\Phi }(t,\sigma )\parallel d\sigma \le \beta \end{array}$

for all t. For time-invariant linear state equations, where Φ(t, σ) = e^A(t−σ), an integration-variable change, in either form of the condition, shows that uniform exponential stability is equivalent to finiteness of

$\begin{array}{l}\hfill {\int }_0^{\infty }\parallel e^{At}\parallel dt.\end{array}$

The adjective “uniform” is superfluous in the time-invariant case, and we will drop it in clear contexts. Though exponential stability usually is called asymptotic stability when discussing time-invariant linear state equations, we retain the term exponential stability.

Combining an explicit representation for e^At with the finiteness condition on Eq. (5.11) yields a better-known characterization of exponential stability.

5.1.2 Uniform asymptotic stability

Note that the elapsed time T, until the solution satisfies the bound (5.13), must be independence of the initial time. Some of the same tools used in proving Theorem 5.1.3 can be used to show that this “elapsed-time uniformity” is the key to uniform exponential stability.

Conversely suppose the state equation is uniformly asymptotically stable. Uniform stability is implied by definition, so there exists a positive γ such that

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t,\tau )\parallel \le \gamma \end{array}$

for all t, τ such that t ≥ τ. Select $\delta =\frac{1}{2}$, and by Definition 5.1.3 let T be such that Eq. (5.13) is satisfied. Then given a t₀, let x_a be such that ∥x_a∥ = 1, and

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t_0+T,t_0)x_a\parallel =\parallel \mathrm{\Phi }(t_0+T,t_0)\parallel .\end{array}$

With the initial state x(t₀) = x_a, the solution of Eq. (5.1) satisfies

$\begin{array}{l}\hfill \begin{array}{cc}\parallel x(t_0+T)\parallel & =\parallel \mathrm{\Phi }(t_0+T,t_0)x_a\parallel \\ & =\parallel \mathrm{\Phi }(t_0+T,t_0)\parallel \parallel x_a\parallel \\ & \le \frac{1}{2}\parallel x_a\parallel \end{array}\end{array}$

from which

$\begin{array}{l}\hfill \parallel \mathrm{\Phi }(t_0+T,t_0)\parallel \le \frac{1}{2}.\end{array}$

Of course such an x_a exists for any given t₀, so the argument compels Eq. (5.15) for any t₀. Now uniform exponential stability is implied by Eqs. (5.14), (5.15), exactly as in the proof of Theorem 5.1.3.

5.1.3 Lyapunov transformation

The stability concepts under discussion are properties of particular linear state equation that presumably represent a system of interest in terms of physically meaningful variables. A basic question involves preservation of stability properties under a state variable change. Since time-varying variable changes are permitted, simple scalar examples can be generated to show that, for example, uniform stability can be created or destroyed by variable change. To circumvent this difficulty we must limit attention to a particular class of state variable changes.

A condition equivalent to Eq. (5.16) is existence of a finite positive constant ρ such that for all t

$\begin{array}{l}\hfill \parallel P(t)\parallel \le \rho ,\parallel P^{-1}(t)\parallel \le \rho .\end{array}$

The lower bound on |detP(t)| implies an upper bound on ∥P⁻¹(t)∥.

Reflecting on the effect of a state variable change on the transition matrix, a detailed proof that Lyapunov transformations preserve stability properties is perhaps belaboring the evident.

The Floquet decomposition for T-periodic state equations provides a general illustration. Since P(t) is the product of a transition matrix and a matrix exponential, it is continuously differentiable with respect to t. Since P(t) is invertible, by continuity arguments there exist ρ, η > 0 such that Eq. (5.16) holds for all t in any P(t) is Lyapunov transformation. It is easy to verify that z(t) = P⁻¹(t)x(t) yields the time-invariant linear state equation

$\begin{array}{l}\hfill Ż(t)=Rz(t).\end{array}$

By this connection stability properties of the original T-periodic state equation are equivalent to stability properties of a time-invariant linear state equation (though, it must be noted, the time-invariant state equation in general is complex).

5.2.1 Introduction

To illustrate the basic idea we consider conditions that imply all solutions of the linear state equation

$\begin{array}{l}\hfill \stackrel{.}{x}(t)=A(t)x(t),x(t_0)=x_0\end{array}$

are such that ∥x(t)∥² monotonically decreases as $t\to \infty$. For any solution x(t) of Eq. (5.19), the derivative of the scalar function

$\begin{array}{l}\hfill \parallel x(t){\parallel }^2=x^T(t)x(t)\end{array}$

with respect to t can be written as

$\begin{array}{l}\hfill \begin{array}{cc}\frac{d}{dt}\parallel x(t){\parallel }^2& ={\stackrel{.}{x}}^T(t)x(t)+x^T(t)\stackrel{.}{x}(t)\\ & =x^T(t)[A^T(t)+A(t)]x(t).\end{array}\end{array}$

In this computation $\stackrel{.}{x}(t)$ is replaced by A(t)x(t) precisely because x(t) is a solution of Eq. (5.19). Suppose that the quadratic form on the right side of Eq. (5.21) is negative definite, that is, suppose the matrix A^T(t) + A(t) is negative definite at each t. Then, as shown in Fig. 5.4, ∥x(t)∥² decreases as t increases. Further we can show that if this negative definiteness does not asymptotically vanish, that is, if there is a constant ν > 0 such that A^T(t) + A(t) ≤−νI for all t, then ∥x(t)∥² goes to zero as $t\to \infty$. Notice that the transition matrix for A(t) is not needed in this calculation, and growth properties of the scalar function (5.20) depend on sign-definiteness properties of the quadratic form in Eq. (5.21). Admittedly this calculation results in a restrictive sufficient condition—negative definiteness of A^T(t) + A(t)—for a type of asymptotic stability. However, more general scalar functions than Eq. (5.20) can be considered.

Formalization of the above discussion involves somewhat intricate definitions of time-dependent quadratic forms that are useful as scalar functions of the state vector of Eq. (5.19) for stability purpose. Such quadratic forms are called quadratic Lyapunov functions. They can be written as x^TQ(t)x, where Q(t) is assumed to be symmetric and continuously differentiable for all t. If x(t) is any solution of Eq. (5.19) for t ≥ t₀, then we are interested in the behavior of the real quantity x^T(t)Q(t)x(t) for t ≥ t₀. This behavior can be assessed by computing the time derivative using the product rule, and replacing $\stackrel{.}{x}(t)$ by A(t)x(t) to obtain

$\begin{array}{l}\hfill \frac{d}{dt}[x^T(t)Q(t)x(t)]=x^T(t)[A^T(t)Q(t)+Q(t)A(t)+\stackrel{.}{Q}(t)]x(t).\end{array}$

To analyze stability properties, various bounds are required on quadratic Lyapunov functions and on the quadratic forms (5.22) that arise as their derivatives along solutions of Eq. (5.19). These bounds can be expressed in alternative ways. For example, the condition that there exists a positive constant η such that

$\begin{array}{l}\hfill Q(t)\ge \eta I\end{array}$

for all t is equivalent by definition to existence of a positive η such that

$\begin{array}{l}\hfill x^{T}Q(t)x\ge \eta \parallel x{\parallel }^2\end{array}$

for all t and all n × 1 vectors x. Yet another way to write this is to require the existence of a symmetric, positive-definite constant matrix M such that

$\begin{array}{l}\hfill x^{T}Q(t)x\ge x^{T}Mx\end{array}$

for all t and all n × 1 vectors x. The choice is largely a matter of taste, and the most economical form is adopted here.

5.2.2 Uniform stability

We begin with a sufficient condition for uniform stability. The presentation style throughout is to list the requirement on Q(t) so that the corresponding quadratic form can be used to prove the desired stability property.

Typically it is profitable to use a quadratic Lyapunov function to obtain stability conditions for linear state equations, rather than a particular instance.

5.2.3 Uniform exponential stability

For n = 2 and constant Q(t) = Q, Theorem 5.22 admits a simple pictorial representation. The condition (5.26) implies that Q is positive definite, and therefore the level curves of the real-valued function x^TQx are ellipses in the (x₁, x₂)-plane. The condition (5.27) implies that for any solution x(t) of the state equation the value of x^T(t)Qx(t) is decreasing as t increases. Thus a plot of the solution x(t) on the (x₁, x₂)-plane crosses smaller-value level curves as t increases, as shown in Fig. 5.5. Under the same assumptions, a similar pictorial interpretation can be given for Theorem 5.2.1. Note that if Q(t) is not constant, the level curves vary with t and the picture is much less informative.

Just in case it appears that stability of linear state equations is reasonably intuitive. A first guess is that the state equation is uniformly exponentially stable if a(t) is continuous and positive for all t, though suspicions might arise if $a(t)\to 0$ as $t\to \infty$. These suspicious would be well founded, but what is more surprising is that there are other obstructions to uniform exponential stability.

The stability criteria provided by the preceding theorems are sufficient conditions that depend on skill in selecting an appropriate Q(t). It is comforting to show that there indeed exists a suitable Q(t) for a large class of uniformly exponentially stable linear state equations. The dark side is that it can be roughly as hard to compute Q(t) as it is to compute the transition matrix for A(t).

5.2.4 Instability

Quadratic Lyapunov function also can be used to develop instability criteria of various types. One example is the following result that, except for one value of t, does not involve a sign-definiteness assumption on Q(t).

One consequence of this inequality, Eq. (5.33), and the choice of x₀ and t₀, is

$\begin{array}{l}\hfill -\rho \parallel x(t){\parallel }^2\le x^{T}Q(t)x(t)\le x_0^{T}Q(t_0)x_0<0,t\ge t_0\end{array}$

and a further consequence is that

$\begin{array}{l}\hfill \begin{array}{cc}\nu {\int }_{t_0}^t{x}^T(\sigma )x(\sigma )d\sigma & \le x_0^{T}Q(t_0)x_0-x^T(t)Q(t)x(t)\\ & \le |x^T(t)Q(t)x(t)|+|x_0^{T}Q(t_0)x_0|\\ & \le 2|x^T(t)Q(t)x(t)|,t\ge t_0.\end{array}\end{array}$

Using Eqs. (5.33), (5.36) gives

$\begin{array}{l}\hfill {\int }_{t_0}^t{x}^T(\sigma )x(\sigma )d\sigma \le \frac{2\rho }{\nu }\parallel x(t){\parallel }^2,t\ge t_0.\end{array}$

The state equation can be shown to be not uniformly stable by proving that x(t) is unbounded. This we do by a contradiction argument. Suppose that there exists a finite γ such that ∥x(t)∥≤ γ, for all t ≥ t₀. Then Eq. (5.37) gives

$\begin{array}{l}\hfill {\int }_{t_0}^t{x}^T(\sigma )x(\sigma )d\sigma \le \frac{2\rho {\gamma }^2}{\nu },t\ge t_0\end{array}$

and the integrand, which is a continuously differentiable scalar function, must go to zero as $t\to 0$. Therefore x(t) must also go to zero, and this implies that Eq. (5.35) is violated for sufficiently large t. The contradiction proves that x(t) cannot be a bounded solution.

5.2.5 Time-invariant case

In the time-invariant case quadratic Lyapunov function with constant Q can be used to connect Theorem 5.2.2 with the familiar eigenvalue condition for exponential stability. If Q is symmetric and positive definite, then Eq. (5.26) is satisfied automatically. However, rather than specifying such a Q and checking to see if a positive ν exists such that Eq. (5.27) is satisfied, the approach can be reversed. Choose a positive definite matrix M, for example M = νI, where ν > 0. If there exists a symmetric, positive-definite Q such that

$\begin{array}{l}\hfill QA+A^{T}Q=-M,\end{array}$

then all the hypotheses of Theorem 5.2.2 are satisfied. Therefore the associated linear state equation

$\begin{array}{l}\hfill \stackrel{.}{x}(t)=Ax(t),x(0)=x_0\end{array}$

is exponentially stable, all eigenvalues of A have negative real parts. Conversely the eigenvalues of A enter the existence question for solution of the Lyapunov equation (5.38).

5.3.1 Uniform bounded-input bounded-output stability

Bounded-input, bounded-output stability is most simply discussed in terms of the largest value (over time) of the norm of the input signal, ∥u(t)∥, in comparison to the largest value of the corresponding response norm ∥y(t)∥. More precisely we use the standard notion of supremum. For example,

$\begin{array}{l}\hfill \nu ={\sup }_{t\ge t_0}\parallel u(t)\parallel \end{array}$

is defined as the smallest constant such that u(t) ≤ ν for t ≥ t₀. If no such bound exists, we write

$\begin{array}{l}\hfill {\sup }_{t\ge t_0}\parallel u(t)\parallel =\infty .\end{array}$

The basic notion is that the zero-state response should exhibit finite “gain” in terms of the input and output suprema.

The adjective “uniform” does double duty in this definition. It emphasizes the fact that the same η works for all values of t₀, and that the same η works for all input signals. An equivalent definition based on the pointwise norms of u(t) and y(t) is explored.

Suppose now that Eq. (5.42) is uniformly bounded-input, bounded-output stable. Then there exists a constant η so that, in particular, the zero-state response for any t₀ and any input signal such that

$\begin{array}{l}\hfill {\sup }_{t\ge t_0}\parallel u(t)\parallel \le 1\end{array}$

satisfies

$\begin{array}{l}\hfill {\sup }_{t\ge t_0}\parallel y(t)\parallel \le \eta .\end{array}$

To set up a contradiction argument, suppose no finite ρ exists that satisfies Eq. (5.45). In other words for any given constant ρ there exist τ_ρ and t_ρ > τ_ρ such that

$\begin{array}{l}\hfill {\int }_{{\tau }_{\rho }}^{t_{\rho }}\parallel G(t_{\rho },\sigma )\parallel d\sigma >\rho .\end{array}$

Taking ρ = η, that there exist τ_η, t_η > τ_η, and indices i, j such that the i, j-entry of the impulse response satisfies

$\begin{array}{l}\hfill {\int }_{{\tau }_{\eta }}^{t_{\eta }}|G_{ij}(t_{\eta },\sigma )|d\sigma >\eta .\end{array}$

With t₀ = τ_η consider the m × 1 input signal u(t) defined for t ≥ t₀ as follows. Set u(t) = 0 for t > t_η, and for t ∈ [t₀, t_η] set every component of u(t) to zero except for the jth-component given by (the piecewise-continuous signal)

$\begin{array}{l}\hfill u_j(t)=\left\{\begin{array}{ll}1& G_{ij}(t_{\eta },t)>0\\ 0& G_{ij}(t_{\eta },t)=0,t\in [t_0,t_{\eta }]\\ -1& G_{ij}(t_{\eta },t)<0.\end{array}\right.\end{array}$

This input signal satisfies ∥u(t)∥≤ 1, for all t ≥ t₀, but the ith-component of the corresponding zero-state response satisfies, by Eq. (5.46),

$\begin{array}{l}\hfill \begin{array}{cc}{y}_i(t_{\eta })& ={\int }_{t_0}^{t_{\eta }}{G}_{ij}(t_{\eta },\sigma )u_j(\sigma )d\sigma \\ & ={\int }_{t_0}^{t_{\eta }}|G_{ij}(t_{\eta },\sigma )|d\sigma \\ & >\eta .\end{array}\end{array}$

Since ∥y(t_η)∥≥∥y_i(t_η)∥, a contradiction is obtained that completes the proof.

An alternate expression for the condition in Theorem 5.3.1 is that there exist a finite ρ such that for all t

$\begin{array}{l}\hfill {\int }_{-\infty }^t\parallel G(t,\sigma )\parallel d\sigma \le \rho .\end{array}$

For a time-invariant linear state equation, G(t, σ) = G(t, −σ), and the impulse response customarily is written as G(t) = Ce^AtB, t ≥ 0. Then a change of integration variable shows that a necessary and sufficient condition for uniform bounded-input, bounded-output stability for a time-invariant state equation is finiteness of the integral

$\begin{array}{l}\hfill {\int }_0^{\infty }\parallel G(t)\parallel dt.\end{array}$

5.3.2 Relation to uniform exponential stability

We now turn to establishing connections between uniform bounded-input, bounded-output stability and the property of uniform exponential stability of the zero-input response.

That coefficient bounds as in Eq. (5.48) are needed to obtain the implication in Lemma 5.3.1 should be clear. However, the simple proof might suggest that uniform exponential stability is a needlessly strong condition for uniform bounded-input, bounded-output stability.

In developing implication of uniform bounded-input, bounded-output stability for uniform exponential stability, we need to strengthen the usual controllability and observability properties. Specifically it will be assumed that these properties are uniform in time in special way. For simplicity, admittedly a commodity in short supply for the next few pages, the development is subdivided into two parts. First we deal with linear state equations where the output is precisely the state vector (C(t) is the n × n identity). In this instance the natural terminology is uniform bounded-input, bounded-state stability.