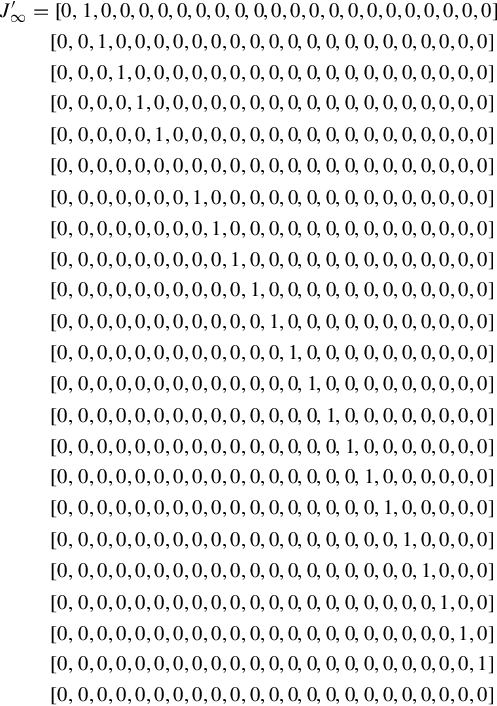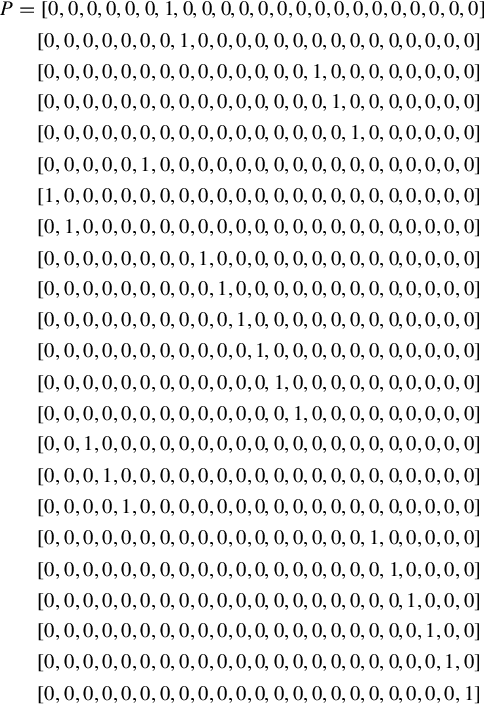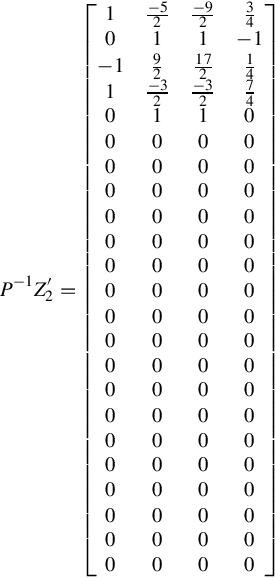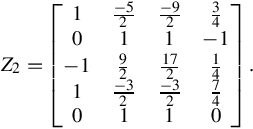J′∞=[0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
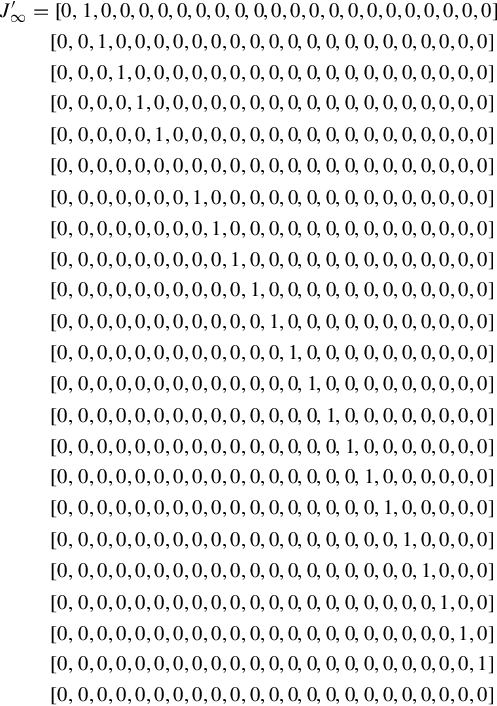 (9.18)
(9.18)
and the infinite Jordan pair (C∞,J∞ ) (in the sense of Vardulakis [13]) of A(s)
) (in the sense of Vardulakis [13]) of A(s)
C∞=⎡⎣⎢⎢⎢⎢02212−1−1001111−1−10−1000⎤⎦⎥⎥⎥⎥,J∞⎡⎣⎢⎢⎢⎢⎢⎢0000010000000000010000010⎤⎦⎥⎥⎥⎥⎥⎥.
It should be noted that the generalized infinite Jordan pair (C′∞,J′∞ ), which has dimensions of 4 × 23 and 23 × 23, is much unnecessarily larger than the infinite Jordan pair (C∞,J∞
), which has dimensions of 4 × 23 and 23 × 23, is much unnecessarily larger than the infinite Jordan pair (C∞,J∞ ) with dimensions of only 4 × 5 and 5 × 5. The following matrix P∈R23×23
) with dimensions of only 4 × 5 and 5 × 5. The following matrix P∈R23×23 is found to delete the redundant information inherited in the generalized infinite Jordan pair.
is found to delete the redundant information inherited in the generalized infinite Jordan pair.
P=[0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0][0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0][0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]
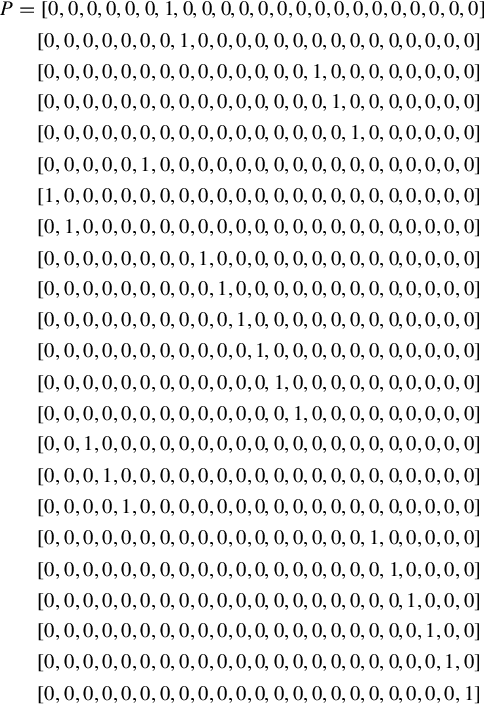
satisfies Theorem 9.2.1. According to Lemma 9.3.2, one has
VS=[A6CJ6,−(A0C′∞(J′∞)6+⋯+A1C′∞J′∞+A2C′∞)]=[0,0,0,0,0,0,34,0,0,−14,1,0,34,0,0,0,12,321128,−62532,0,12,−14,−14,−14,−14,−34,−321128,3013128][0,0,0,0,0,0,12,0,0,0,12,0,12,0,0,0,0,−12,−41764,0,14,−14,−14,−14,−14,−14,14,46564][0,0,0,0,0,0,0,0,0,0,−14,0,0,0,0,0,0,0,385128,0,0,0,0,0,0,0,0,−417128][0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,−1,0,0,0,0,0,0,0,0,1]=⎡⎣⎢⎢⎢C⋮CJ5C′∞(J′∞)5⋮C′∞⎤⎦⎥⎥⎥=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,1,−1,−1][1,0,0,0,0,0,0,0,0,0,94,0,0,0,0,0,2,−1,−385128,0,0,0,0,0,1,−1,0,417128][1,0,0,1,0,0,0,0,0,0,2,0,0,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0][1,1,0,1,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0][0,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,0,0,1,−1,−1,−1][1,0,0,0,0,0,0,0,0,94,−32,0,0,0,0,2,−1,−385128,68932,0,0,0,0,1,−1,0,417128,−3173128][1,0,0,−1,0,0,0,0,0,2,−10,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0,0][1,1,1,−1,−1,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0][0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,0,0,1,−1,−1,−1,−1][1,0,0,0,0,0,0,0,94,−32,−385128,0,0,0,2,−1,−385128,68932,−362164,0,0,0,1,−1,0,417128,−3173128,8683128][1,0,0,1,0,0,0,0,2,−1,0,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0,0,0][1,1,2,1,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0][0,0,0,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,0,0,1,−1,−1,−1,−1,−1][1,0,0,0,0,0,0,94,−32,−385128,70532,0,0,2,−1,−385128,68932,−362164,149416,0,0,1,−1,0,417128,−3173128,8683128,−9731128][1,0,0,−1,0,0,0,2,−1,0,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0,0,0,0][1,1,3,−1,−1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0][0,0,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,−2,0,0,1,−1,−1,−1,−1,−1,1][1,0,0,0,0,0,94,−32,−385128,70532,−360564,0,2,−1,−385128,68932,−362164,149316,−8623128,0,1,−1,0,417128,−3173128,8683128,−9731128,−108964][1,0,0,1,0,0,2,−1,0,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0,0,0,0,0][1,1,4,1,1,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0][0,0,0,0,0,0,2,0,0,0,1,0,2,0,0,0,0,−2,−44932,0,1,−1,−1,−1,−1,−1,1,38532][1,0,0,0,0,94,−32,−385128,70532,−360564,148516,2,−1,−385128,68932,−362164,149316,−8623128,−121532,1,−1,0,417128,−3173128,8683128,−9731128,−108964,507564][1,0,0,−1,0,2,−1,0,0,0,0,2,−1,0,0,0,0,0,0,1,−1,0,0,0,0,0,0,0][1,1,5,−1,−1,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0].
so from
 (9.19)
(9.19)
and from
P−1Z′2=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢10−110000000000000000000−52192−321000000000000000000−921172−32100000000000000000034−114740000000000000000000⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥
one obtains
Z2=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢10−110−52192−321−921172−32134−114740⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥.
Hence, by Theorem 9.3.1 we have constructed the refined resolvent decomposition for the regular polynomial matrix A(s) as follows
![]() ,
, ![]() , and Z2 have the minimal dimensions of 4 × 5, 5 × 5, and 5 × 4. Compared to the resolvent decomposition of Gohberg et al. [17] given by
, and Z2 have the minimal dimensions of 4 × 5, 5 × 5, and 5 × 4. Compared to the resolvent decomposition of Gohberg et al. [17] given by
![]() ,
, ![]() , and
, and ![]() are given by Eqs. (9.17), (9.18), (9.19), respectively, due to the fact that the redundant information has been deleted, the above refined resolvent decomposition is obviously in a much more concise form, which will definitely bring some convenience when applied to the solution of the regular PMDs.
are given by Eqs. (9.17), (9.18), (9.19), respectively, due to the fact that the redundant information has been deleted, the above refined resolvent decomposition is obviously in a much more concise form, which will definitely bring some convenience when applied to the solution of the regular PMDs.![]() in Eq. (9.3) are formulated explicitly, which means this method is constructive. The main idea in this proposed approach is to calculate an elementary matrix P, which is very easy to obtain, to delete the redundant information, then to propose the refined resolvent decomposition. This elementary matrix has the effect of deleting the redundant information in two ways. First, it deletes the redundant information in those blocks in the infinite Jordan pair of Gohberg et al. [17] that correspond to the infinite zeros and bring them into the correct sizes. Second, it deletes the whole blocks in the infinite Jordan pair of Gohberg et al. [17] that correspond to the infinite poles and the whole blocks that are not dynamically important. This elementary matrix serves to transform the partitioned block matrix in
in Eq. (9.3) are formulated explicitly, which means this method is constructive. The main idea in this proposed approach is to calculate an elementary matrix P, which is very easy to obtain, to delete the redundant information, then to propose the refined resolvent decomposition. This elementary matrix has the effect of deleting the redundant information in two ways. First, it deletes the redundant information in those blocks in the infinite Jordan pair of Gohberg et al. [17] that correspond to the infinite zeros and bring them into the correct sizes. Second, it deletes the whole blocks in the infinite Jordan pair of Gohberg et al. [17] that correspond to the infinite poles and the whole blocks that are not dynamically important. This elementary matrix serves to transform the partitioned block matrix in ![]() that corresponds to the redundant information into zero, the resulting refined resolvent decomposition is thus of minimal dimensions. Further, by using this elementary matrix the mechanism of decoupling in the solution of Gohberg et al. [17] is explained clearly. This refined resolvent decomposition facilitates computation of the inverse matrix of A(s) due to the fact that the dimensions of the matrices used are minimal. Once the refined resolvent decomposition is obtained, the generalized infinite Jordan pair and the elementary matrix P are no longer needed in the calculation of the solution of the regular PMD. This therefore presents another merit to this method, which is algorithmically attractive when applied in actual computation.
that corresponds to the redundant information into zero, the resulting refined resolvent decomposition is thus of minimal dimensions. Further, by using this elementary matrix the mechanism of decoupling in the solution of Gohberg et al. [17] is explained clearly. This refined resolvent decomposition facilitates computation of the inverse matrix of A(s) due to the fact that the dimensions of the matrices used are minimal. Once the refined resolvent decomposition is obtained, the generalized infinite Jordan pair and the elementary matrix P are no longer needed in the calculation of the solution of the regular PMD. This therefore presents another merit to this method, which is algorithmically attractive when applied in actual computation.